Opencv 三次样条曲线(Cubic Spline)插值

本系列文章由 @YhL_Leo 出品，转载请注明出处。
文章链接： http://blog.csdn.net/yhl_leo/article/details/47707679

1.样条曲线简介

样条曲线(Spline)本质是分段多项式实函数，在实数范围内有： S:[a,b]→R ，在区间 [a,b] 上包含 k 个子区间 [ti−1,ti] ，且有：

a=t0<t1<⋯<tk−1<tk=b(1)

对应每一段区间 i 的存在多项式： Pi:[ti−1,ti]→R ，且满足于：

S(t)=P1(t) , t0≤t<t1,S(t)=P2(t) , t1≤t<t2,⋮S(t)=Pk(t) , tk−1≤t≤tk.(2)

其中， Pi(t) 多项式中最高次项的幂，视为样条的阶数或次数（Order of spline），根据子区间 [ti−1,ti] 的区间长度是否一致分为均匀（Uniform）样条和非均匀（Non-uniform）样条。

满足了公式 (2) 的多项式有很多，为了保证曲线在 S 区间内具有据够的平滑度，一条 n 次样条，同时应具备处处连续且可微的性质：

P(j)i(ti)=P(j)i+1(ti);(3)

其中 i=1,…,k−1;j=0,…,n−1 。

2.三次样条曲线

2.1曲线条件

按照上述的定义，给定节点：

t:z:a=t0z0<t1z1<⋯⋯<tk−1zk−1<tkzk=b(4)

三次样条曲线满足三个条件：

1. 在每段分段区间 [ti,ti+1],i=0,1,…,k−1 上， S(t)=Si(t) 都是一个三次多项式；
2. 满足 S(ti)=zi,i=1,…,k−1 ;
3. S(t) 的一阶导函数 S′(t) 和二阶导函数 S′′(t) 在区间 [a,b]上都是连续的，从而曲线具有光滑性。

则三次样条的方程可以写为：

Si(t)=ai+bi(t−ti)+ci(t−ti)2+di(t−ti)3,(5)

其中， ai,bi,ci,di 分别代表 n 个未知系数。

• 曲线的连续性表示为：

Si(ti)=zi,(6)

Si(ti+1)=zi+1,(7)

其中 i=0,1,…,k−1 。

• 曲线微分连续性：

S′i(ti+1)=S′i+1(ti+1),(8)

S′′i(ti+1)=S′′i+1(ti+1),(9)

其中 i=0,1,…,k−2 。

• 曲线的导函数表达式：

S′i=bi+2ci(t−ti)+3di(t−ti)2,(10)

S′′i(x)=2ci+6di(t−ti),(11)

令区间长度 hi=ti+1−ti ，则有：

1. 由公式 (6) ，可得： ai=zi ；

2. 由公式 (7) ，可得： ai+bihi+cih2i+dih3i=zi+1 ；

3. 由公式 (8) ，可得：
   S′i(ti+1)=bi+2cihi+3dih2i ;
   S′i+1(ti+1)=bi+1 ；
   ⇒bi+2cihi+3dih2i−bi+1=0 ；

4. 由公式 (9) ，可得：
   S′′i(ti+1)=2ci+6dihi ；
   S′′i+1(ti+1)=2ci+1 ；
   ⇒2ci+6dihi=2ci+1 ；

   设 mi=S′′i(xi)=2ci ，则：

   A. mi+6dihi−mi+1=0⇒
   di=mi+1−mi6hi ；

   B.将 ci,di 代入 zi+bihi+cih2i+dih3i=zi+1⇒
   bi=zi+1−zihi−hi2mi−hi6(mi+1−mi) ；

   C.将 bi,ci,di 代入 bi+2cihi+3dih2i=bi+1⇒
   

   himi+2(hi+hi+1)mi+1+hi+1mi+2=6[zi+2−zi+1hi+1−zi+1−zihi].(12)

2.2端点条件

在上述分析中，曲线段的两个端点 t0 和 tk 是不适用的，有一些常用的端点限制条件，这里只讲解自然边界。
在自然边界下，首尾两端的二阶导函数满足 S′′=0 ，即 m0=0 和 mn=0 ，求解方程组可写为：

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢1h00⋮002(h0+h1)h2…0h12(h1+h2)⋱00h2⋱hk−20…0⋱2(hk−2+hk−1)00⋮hk−11⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢m0m1m2⋮mk−1mk⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥=6⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢0z2−z1h1−z1−z0h0z3−z2h2−z2−z1h1⋮zk−zk−1hk−1−zk−1−zk−2hk−20⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥(13)

其系数矩阵为三对角线矩阵，在该篇博客内会有其讲解。

3.Code

// CubicSplineInterpolation.h

/* Cubic spline interpolation class. - Editor: Yahui Liu. - Data: 2015-08-16 - Email: [email protected] - Address: Computer Vision and Remote Sensing(CVRS), Lab. */

#ifndef CUBIC_SPLINE_INTERPOLATION_H
#pragma once
#define CUBIC_SPLINE_INTERPOLATION_H

#include <iostream>
#include <vector>
#include <math.h>

#include <cv.h>
#include <highgui.h>

using namespace std;
using namespace cv;

/* Cubic spline interpolation coefficients */
class CubicSplineCoeffs
{
public:
    CubicSplineCoeffs( const int &count ) 
    {
        a = std::vector<double>(count);
        b = std::vector<double>(count);
        c = std::vector<double>(count);
        d = std::vector<double>(count);
    }
    ~CubicSplineCoeffs() 
    {
        std::vector<double>().swap(a);
        std::vector<double>().swap(b);
        std::vector<double>().swap(c);
        std::vector<double>().swap(d);
    }

public:
    std::vector<double> a, b, c, d;
};

enum CubicSplineMode
{
    CUBIC_NATURAL,    // Natural
    CUBIC_CLAMPED,    // TODO: Clamped 
    CUBIC_NOT_A_KNOT  // TODO: Not a knot 
};

enum SplineFilterMode
{
    CUBIC_WITHOUT_FILTER, // without filter
    CUBIC_MEDIAN_FILTER  // median filter
};

/* Cubic spline interpolation */
class CubicSplineInterpolation
{
public:
    CubicSplineInterpolation() {}
    ~CubicSplineInterpolation() {}

public:

    /* Calculate cubic spline coefficients. - node list x (input_x); - node list y (input_y); - output coefficients (cubicCoeffs); - ends mode (splineMode). */
    void calCubicSplineCoeffs( std::vector<double> &input_x, 
        std::vector<double> &input_y, CubicSplineCoeffs *&cubicCoeffs,
        CubicSplineMode splineMode = CUBIC_NATURAL,
        SplineFilterMode filterMode = CUBIC_MEDIAN_FILTER );

    /* Cubic spline interpolation for a list. - input coefficients (cubicCoeffs); - input node list x (input_x); - output node list x (output_x); - output node list y (output_y); - interpolation step (interStep). */
    void cubicSplineInterpolation( CubicSplineCoeffs *&cubicCoeffs,
        std::vector<double> &input_x, std::vector<double> &output_x,
        std::vector<double> &output_y, const double interStep = 0.5 );

    /* Cubic spline interpolation for a value. - input coefficients (cubicCoeffs); - input a value(x); - output interpolation value(y); */
    void cubicSplineInterpolation2( CubicSplineCoeffs *&cubicCoeffs,
        std::vector<double> &input_x, double &x, double &y );

    /* calculate tridiagonal matrices with Thomas Algorithm(TDMA) : example: | b1 c1 0 0 0 0 | |x1 | |d1 | | a2 b2 c2 0 0 0 | |x2 | |d2 | | 0 a3 b3 c3 0 0 | |x3 | = |d3 | | ... ... | |...| |...| | 0 0 0 0 an bn | |xn | |dn | Ci = ci/bi , i=1; ci / (bi - Ci-1 * ai) , i = 2, 3, ... n-1; Di = di/bi , i=1; ( di - Di-1 * ai )/(bi - Ci-1 * ai) , i = 2, 3, ..., n-1 xi = Di - Ci*xi+1 , i = n-1, n-2, 1; */
    bool caltridiagonalMatrices( cv::Mat_<double> &input_a, 
        cv::Mat_<double> &input_b, cv::Mat_<double> &input_c,
        cv::Mat_<double> &input_d, cv::Mat_<double> &output_x );

    /* Calculate the curve index interpolation belongs to */
    int calInterpolationIndex( double &pt, std::vector<double> &input_x );

    /* median filtering */
    void cubicMedianFilter( std::vector<double> &input, const int filterSize = 5 );

    double cubicSort( std::vector<double> &input );
    // double cubicNearestValue( std::vector );
};

#endif // CUBIC_SPLINE_INTERPOLATION_H

// CubicSplineInterpolation.cpp

#include "CubicSplineInterpolation.h"

void CubicSplineInterpolation::calCubicSplineCoeffs( 
    std::vector<double> &input_x, 
    std::vector<double> &input_y, 
    CubicSplineCoeffs *&cubicCoeffs,
    CubicSplineMode splineMode /* = CUBIC_NATURAL */,
    SplineFilterMode filterMode /*= CUBIC_MEDIAN_FILTER*/ )
{
    int sizeOfx = input_x.size();
    int sizeOfy = input_y.size();

    if ( sizeOfx != sizeOfy )
    {
        std::cout << "Data input error!" << std::endl <<
            "Location: CubicSplineInterpolation.cpp" <<
            " -> calCubicSplineCoeffs()" << std::endl;

        return;
    }

    /* hi*mi + 2*(hi + hi+1)*mi+1 + hi+1*mi+2 = 6{ (yi+2 - yi+1)/hi+1 - (yi+1 - yi)/hi } so, ignore the both ends: | - - - 0 ... 0 | |m0 | | h0 2(h0+h1) h1 0 ... 0 | |m1 | | 0 h1 2(h1+h2) h2 0 ... | |m2 | | ... ... 0 | |...| | 0 ... 0 h(n-2) 2(h(n-2)+h(n-1)) h(n-1) | | | | 0 ... ... - | |mn | */

    std::vector<double> copy_y = input_y;

    if ( filterMode == CUBIC_MEDIAN_FILTER )
    {
        cubicMedianFilter(copy_y, 5);
    }

    const int count  = sizeOfx;
    const int count1 = sizeOfx - 1;
    const int count2 = sizeOfx - 2;
    const int count3 = sizeOfx - 3;

    cubicCoeffs = new CubicSplineCoeffs( count1 );

    std::vector<double> step_h( count1, 0.0 );

    // for m matrix
    cv::Mat_<double> m_a(1, count2, 0.0);
    cv::Mat_<double> m_b(1, count2, 0.0);
    cv::Mat_<double> m_c(1, count2, 0.0);
    cv::Mat_<double> m_d(1, count2, 0.0);
    cv::Mat_<double> m_part(1, count2, 0.0);

    cv::Mat_<double> m_all(1, count, 0.0);

    // initial step hi
    for ( int idx=0; idx < count1; idx ++ )
    {
        step_h[idx] = input_x[idx+1] - input_x[idx];
    }
    // initial coefficients
    for ( int idx=0; idx < count3; idx ++ )
    {
        m_a(idx) = step_h[idx];
        m_b(idx) = 2 * (step_h[idx] + step_h[idx+1]);
        m_c(idx) = step_h[idx+1];
    }
    // initial d
    for ( int idx =0; idx < count3; idx ++ )
    {
        m_d(idx) = 6 * ( 
            (copy_y[idx+2] - copy_y[idx+1]) / step_h[idx+1] -  
            (copy_y[idx+1] - copy_y[idx]) / step_h[idx] );
    }

     //cv::Mat_<double> matOfm( count2, )
    bool isSucceed = caltridiagonalMatrices(m_a, m_b, m_c, m_d, m_part);
    if ( !isSucceed )
    {
        std::cout<<"Calculate tridiagonal matrices failed!"<<std::endl<<
            "Location: CubicSplineInterpolation.cpp -> " <<
            "caltridiagonalMatrices()"<<std::endl;

        return;
    }

    if ( splineMode == CUBIC_NATURAL )
    {
        m_all(0)      = 0.0;
        m_all(count1) = 0.0;

        for ( int i=1; i<count1; i++ )
        {
            m_all(i) = m_part(i-1);
        }

        for ( int i=0; i<count1; i++ )
        {
            cubicCoeffs->a[i] = copy_y[i];
            cubicCoeffs->b[i] = ( copy_y[i+1] - copy_y[i] ) / step_h[i] -
                step_h[i]*( 2*m_all(i) + m_all(i+1) ) / 6;
            cubicCoeffs->c[i] = m_all(i) / 2.0;
            cubicCoeffs->d[i] = ( m_all(i+1) - m_all(i) ) / ( 6.0 * step_h[i] );
        }
    }
    else
    {
        std::cout<<"Not define the interpolation mode!"<<std::endl;
    }
}

void CubicSplineInterpolation::cubicSplineInterpolation( 
    CubicSplineCoeffs *&cubicCoeffs,
    std::vector<double> &input_x,
    std::vector<double> &output_x,
    std::vector<double> &output_y, 
    const double interStep )
{
    const int count = input_x.size();

    double low  = input_x[0];
    double high = input_x[count-1];

    double interBegin = low;
    for ( ; interBegin < high; interBegin += interStep )
    {
        int index = calInterpolationIndex(interBegin, input_x);
        if ( index >= 0 )
        {
            double dertx = interBegin - input_x[index];
            double y = cubicCoeffs->a[index] + cubicCoeffs->b[index] * dertx +
                cubicCoeffs->c[index] * dertx * dertx + 
                cubicCoeffs->d[index] * dertx * dertx * dertx;
            output_x.push_back(interBegin);
            output_y.push_back(y);
        }
    }
}

void CubicSplineInterpolation::cubicSplineInterpolation2( 
    CubicSplineCoeffs *&cubicCoeffs,
    std::vector<double> &input_x, double &x, double &y)
{
    const int count = input_x.size();

    double low  = input_x[0];
    double high = input_x[count-1];

    if ( x<low || x>high )
    {
        std::cout<<"The interpolation value is out of range!"<<std::endl;
    }
    else
    {
        int index = calInterpolationIndex(x, input_x);
        if ( index > 0 )
        {
            double dertx = x - input_x[index];
            y = cubicCoeffs->a[index] + cubicCoeffs->b[index] * dertx +
                cubicCoeffs->c[index] * dertx * dertx + 
                cubicCoeffs->d[index] * dertx * dertx * dertx;
        }
        else
        {
            std::cout<<"Can't find the interpolation range!"<<std::endl;
        }
    }
}

bool CubicSplineInterpolation::caltridiagonalMatrices( 
    cv::Mat_<double> &input_a, 
    cv::Mat_<double> &input_b, 
    cv::Mat_<double> &input_c,
    cv::Mat_<double> &input_d,
    cv::Mat_<double> &output_x )
{
    int rows = input_a.rows;
    int cols = input_a.cols;

    if ( ( rows == 1 && cols > rows ) || 
        (cols == 1 && rows > cols ) )
    {
        const int count = ( rows > cols ? rows : cols ) - 1;

        output_x = cv::Mat_<double>::zeros(rows, cols);

        cv::Mat_<double> cCopy, dCopy;
        input_c.copyTo(cCopy);
        input_d.copyTo(dCopy);

        if ( input_b(0) != 0 )
        {
            cCopy(0) /= input_b(0);
            dCopy(0) /= input_b(0);
        }
        else
        {
            return false;
        }

        for ( int i=1; i < count; i++ )
        {
            double temp = input_b(i) - input_a(i) * cCopy(i-1);
            if ( temp == 0.0 )
            {
                return false;
            }

            cCopy(i) /= temp;
            dCopy(i) = ( dCopy(i) - dCopy(i-1)*input_a(i) ) / temp;
        }

        output_x(count) = dCopy(count);
        for ( int i=count-2; i > 0; i-- )
        {
            output_x(i) = dCopy(i) - cCopy(i)*output_x(i+1);
        }
        return true;
    }
    else
    {
        return false;
    }
}

int CubicSplineInterpolation::calInterpolationIndex( 
    double &pt, std::vector<double> &input_x )
{
    const int count = input_x.size()-1;
    int index = -1;
    for ( int i=0; i<count; i++ )
    {
        if ( pt > input_x[i] && pt <= input_x[i+1] )
        {
            index = i;
            return index;
        }
    }
    return index;
}

void CubicSplineInterpolation::cubicMedianFilter( 
    std::vector<double> &input, const int filterSize /* = 5 */ )
{
    const int count = input.size();
    for ( int i=filterSize/2; i<count-filterSize/2; i++ )
    {
        std::vector<double> temp(filterSize, 0.0);
        for ( int j=0; j<filterSize; j++ )
        {
            temp[j] = input[i+j - filterSize/2];
        }

        input[i] = cubicSort(temp);

        std::vector<double>().swap(temp);
    }

    for ( int i=0; i<filterSize/2; i++ )
    {
        std::vector<double> temp(filterSize, 0.0);
        for ( int j=0; j<filterSize; j++ )
        {
            temp[j] = input[j];
        }

        input[i] = cubicSort(temp);
        std::vector<double>().swap(temp);
    }

    for ( int i=count-filterSize/2; i<count; i++ )
    {
        std::vector<double> temp(filterSize, 0.0);
        for ( int j=0; j<filterSize; j++ )
        {
            temp[j] = input[j];
        }

        input[i] = cubicSort(temp);
        std::vector<double>().swap(temp);
    }
}

double CubicSplineInterpolation::cubicSort( std::vector<double> &input )
{
    int iCount = input.size();
    for ( int j=0; j<iCount-1; j++ )
    {
        for ( int k=iCount-1; k>j; k-- )
        {
            if ( input[k-1] > input[k] )
            {
                double tp  = input[k];
                input[k]   = input[k-1];
                input[k-1] = tp;
            }
        }
    }
    return input[iCount/2];
}

// main.cpp

#include "CubicSplineInterpolation.h"

void main()
{
    double x[22] = {
        926.500000,
        928.000000,
        929.500000,
        931.000000,
        932.500000,
        934.000000,
        935.500000,
        937.000000,
        938.500000,
        940.000000,
        941.500000,
        943.000000,
        944.500000,
        946.000000,
        977.500000,
        980.500000,
        982.000000,
        983.500000,
        985.000000,
        986.500000,
        988.000000,
        989.500000};

    double y[22] = {
        381.732239,
        380.670530,
        380.297786,
        379.853896,
        379.272647,
        378.368584,
        379.319757,
        379.256485,
        380.233150,
        378.183257,
        377.543639,
        376.948999,
        376.253935,
        198.896327,
        670.369434,
        374.273702,
        372.498821,
        373.149402,
        372.139661,
        372.510891,
        372.772791,
        371.360553};

    std::vector<double> input_x(22), input_y(22);
    for ( int i=0; i<22; i++)
    {
        input_x[i] = x[i];
        input_y[i] = y[i];
    }


    CubicSplineCoeffs *cubicCoeffs;
    CubicSplineInterpolation cubicSpline;
    cubicSpline.calCubicSplineCoeffs(input_x, input_y, cubicCoeffs, CUBIC_NATURAL, CUBIC_MEDIAN_FILTER);

   std::vector<double> output_x, output_y;
   cubicSpline.cubicSplineInterpolation( cubicCoeffs, input_x, output_x, output_y );

    double xx(946.0), yy(0.0);
    cubicSpline.cubicSplineInterpolation2(cubicCoeffs, input_x, xx, yy);
    std::cout<<yy<<std::endl;

    std::ofstream outfile( "E:\\test.txt", std::ios::out );
    if ( outfile )
    {
        for ( int i=0; i<output_y.size(); i++ )
        {
            outfile<<std::fixed<<setprecision(3)<<output_x[i]<<" "<<output_y[i]<<std::endl;
        }
    }
    outfile.close();
}

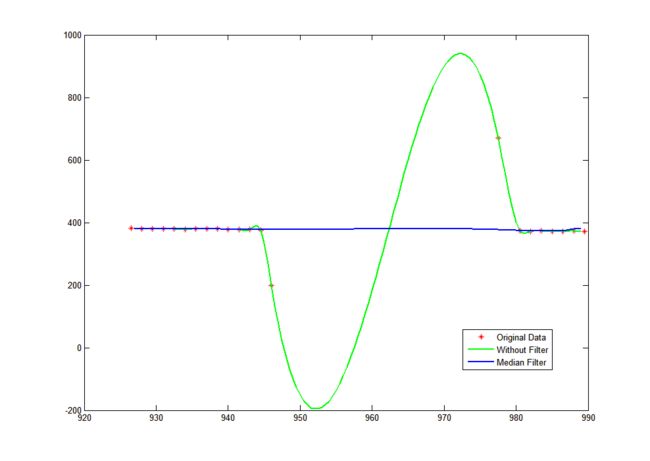
运行结果：

插值点集如图所示：

其中单独点插值的运行结果分别为：

198.896 // yy, CUBIC_WITHOUT_FILTER
376.949 // yy, CUBIC_MEDIAN_FILTER

参考文献：
1.https://en.wikipedia.org/wiki/Spline_(mathematics)
2.http://www.cnblogs.com/xpvincent/archive/2013/01/26/2878092.html