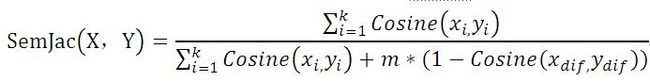穷人的语义处理工具箱之一:语义版Jaccard
author: 张俊林
|为什么我们是ML界的穷人
如果对工业界里的机器学习(ML)从业者进行阶级划分的话,划线标准不是你用的算法的学名听起来多酷炫,无论你手里抡着的是最潮的深度高达1000层的深度学习核炸弹,还是听起来有点掉渣的大刀长矛朴素贝叶斯,如果没有大量数据,尤其是能跑监督学习算法的带标签训练数据,你就是ML界标准的底层渣男渣女或者渣娘炮。再加上计算资源,如果贵公司有上千台GPU服务器集群可供阁下驱使,外加十几火车皮的训练数据,那你就可能成为ML界的新贵、大数据处理领域的马云。
但是,理想丰满现实骨感,大多数中小公司里ML界贫农们的日常生活写照是这样的:前一天晚上看到某篇论文,学到一个让人兴味盎然的新ML姿势,第二天一大早横刀立马豪气干云地冲到公司,热血沸腾血往上涌准备撸起袖子大干一场,但是一转念掰着指头数数,看看自己手上超不过手指数量的数据资源,顿生有心杀贼,无力回天的挫败感。这画面的美丽程度与“看不进书的时候照照镜子,加不了班的时候数数银行卡余额”有异曲同工之妙。
但是穷人也应该有一颗追求美和好好活下去的强大心脏,既然没有训练数据,那我们就好好玩无监督学习,老老实实地去拟合你想要的公式,俗话说得好:无产阶级打破的只有枷锁,而得到的是整个世界。而本文就是带给ML界底层农民工的礼物和福音。
好,安利部分到此为止,以下是正文。
原生态Jaccard作为相似性计算函数,无论是计算思想还是工程实现都简单得令人发指。假设有两个集合:集合A和集合B,每个集合内各自包含若干元素,那么Jaccard计算两个集合的相似性就是用两个集合元素的交集作为分子,两个集合元素的并集作为分母,除一下就完事。因为交集代表了两个集合相同部分的子集合,并集代表了两个集合加起来总共有多少个元素,用相同部分占总元素数比例来代表集合相似性,两者重叠部分越多则两个集合越相似。
在文本处理领域,Jaccard也是一个比较常用的计算句子相似性的工具。具体使用时,往往是把两个要计算相似程度的句子改造成n-gram片段组成的两个集合,然后通过计算两个集合相同的n-gram片段个数作为集合交集,两个集合合并后的n-gram片段个数作为集合并集,这样就能得出两个句子的相似性得分。比如下面两个句子:
句子A:苹果电脑的价格
句子B:苹果ipad的价格
两个句子转换为2-gram后,形成如下集合:
SetA={苹果,果电,电脑,脑的,的价,价格}
SetB={苹果,果ipad,ipad的,的价,价格}
两个集合求交集得出相同语言片段个数为:3.(即为:苹果,的价,价格)
两个集合求并集得出分母大小为:8
所以这两个句子的相似度为:3/8=0.375
在Jaccard的世界里,一切都是这么简单,智商80以上人群看完之后都会会心一笑,此刻,他们的眼里闪耀着智慧的光芒。
原生态Jaccard得分由于过于简单,在计算相似性只用Jaccard的情形比较少,但是往往会被用来作为机器学习系统的一个比较重要的特征因子,很多NLP领域的评测方法也参考这个思想,比如机器翻译评测方法BLUE,文本摘要评测方法ROUGE-N等本质上就是类似于Jaccard的思想,其实语义Jaccard对传统Jaccard的改进思路也可以试着用来改造BLUE或者ROUGE-N评价标准,当然如果实验证明没效果就当我没说这句话。
|语义版Jaccard的诞生
公元2015年的第一场雪,来得比往年早了一些。镜头摇近,一位面容憔悴衣衫落魄的中年男子(注1:不是杜甫,是本文作者)飘入画面,他深深地吸入一口帝都醇厚甘冽的雾霾,由于吸得生猛,只见他虎躯一震,止不住干咳两声,背手望着空中漫天纷扬飞舞的细雪,诗兴大发,正要蹦出:“月是故乡明,霾是故都纯,黄狗身上白,白狗身上肿”这首情景交融感人至深的千古咏雪名句。突然间,一个诡异的念头飘入他的脑中:经典Jaccard只是衡量两个句子字面上的文本匹配程度,如果用语义相似性替代字面相似性来改造一下Jaccard,那么在处理文本的时候是否会更有效些呢?
这是一个好问题。
很明显,引入语义版Jaccard后可以对传统使用字面版本匹配的Jaccard进行改进,因为此时是在文本的语义空间进行的匹配,而非单独字面匹配,应该会引入更多信息量。比如:
句子A:请问苹果电脑的价格
句子B:问下联想笔记本多少钱
如果用3-gram构造句子集合片段的话,很容易看出来字面匹配版Jaccard算出的相似性为0,因为两者没有任何字面上匹配的三元组片段。但是很明显地,我们可以看出下面的单词之间语义相似度是非常高的:
请问vs问下
苹果vs联想
电脑vs笔记本
价格vs多少钱
那么我们现在面临的问题是:能否对传统只进行字面匹配的Jaccard进行改造,使得两个句子能够进行语义级别的匹配计算?即可以将“电脑”/“笔记本”这种字面不匹配但是语义匹配的情况考虑进去,这是触发那位中年男子头脑中语义版Jaccard的最初想法。
|语义版Jaccard
经过一番推敲试错调整,最终定稿的语义版Jaccard具体计算公式如下:
我知道,这个公式看上去有点丑陋,但请耐心让我把话说完。
上述公式中,分子部分代表两个句子语言片段组成集合的语义交集:即语义相似性部分,而分母代表两个句子语言片段组成集合的语义并集,又可分为两部分:第一个部分和分子一样,代表语义交集,而第二个部分代表这两个集合的语义差异程度,两者之和形成集合并集。
1.语义相似性部分(分子)如何计算
为了便于画图与说明,我们拿以下短语为例子来说明语义版Jaccard公式的分子是如何计算出来的。真实应用场景中句子长度可以不做这种长度限制。
SentenceA: 电脑多少钱
SentenceB:计算机的价格
第一步: 把SentenceA切割成3-gram表达形式,于是SentenceA变成如下形式
SetA={电脑多,脑多少,多少钱}
第二步:把SentenceB切割成3-gram表达形式,于是SentenceB变成如下形式
SetB={计算机,算机价,机价格}
第三步:构造相似性矩阵:以句子长度比较短的句子集合元素作为矩阵纵坐标,较长的句子集合元素作为横坐标,改造为如下矩阵:
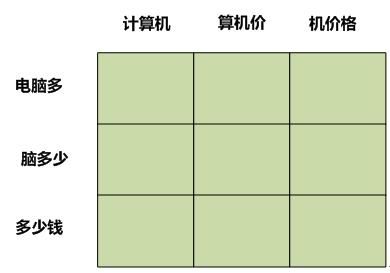
第四步:用横坐标和纵坐标对应的语言片段的语义相似性填充矩阵元素值。首先可以用Word2Vec训练出每个汉字的Word Embedding,也就是其低维向量表示,一定程度上代表其包含的语义信息。那么3-gram包含了三个汉字,这3-gram的语义向量Word Embedding该怎么表示?可以简单粗暴地把其三个汉字的Word Embedding相应维度上的值累加求和即可。
这样两个3-gram片段对应的Word Embedding都有了,剩下的就简单了,它们两个的语义相似性直接用Cosine计算两个Word Embedding在语义空间的向量夹角就成,一般语义越相似,Cosine得分越大。填充好的矩阵形式如下:
第五步:填好相似性矩阵值是基础工作,做完之后,让我们正式开始计算语义版Jaccard公式的分子部分。
首先,先拍脑袋选出一个阈值a=0.6,意思是在计算语义相似性的时候,如果语言片段相似性高于阈值,我们认为两个语言片段语义匹配,这个阈值可以用来控制计算结束过程。算法描述如下。
算法:语义Jaccard相似性部分计算;
输入:语义相似性矩阵S,阈值a;
输出:语义Jaccard公式分子部分分值Total
步骤:
循环如下步骤,直到算法退出:
Step 1.找到相似性矩阵S中的当前所有元素中的最高值;
Step 2.如果这个最高值高于阈值a,则累加到Total中,转步骤3;
如果这个最高值低于阈值,则分子部分计算结束,输出Total值;
Step 3.把当前矩阵中的最高值对应矩阵横坐标和纵坐标的行及列中所有元素值置为0,其含义是这两个片段不再参与后面的计算了,然后返回Step 1步骤继续循环;
在我们上面给出的例子中,如果遵循上述算法流程,则如是循环:
1. 分子总分Total=0;我们假设阈值a取0.8;
2.首先找到矩阵中的最高值:坐标[1,1]对应的0.99,其代表片段“电脑多”和“计算机”的片段语义相似性,发现其大于阈值0.8,那么累积分子得分,更新Total值:Total=0.99;
3.将矩阵中第一行和第一列所有元素相似性置为0,则当前形成下图:

4.然后在矩阵剩下的元素里面找到最高值:坐标[3,3]对应的0.98,其代表片段“多少钱”和“的价格”的片段语义相似性,发现其值大于阈值0.8,那么累积分子得分,更新Total值:
Total=0.99+0.98=1.97
5.将矩阵中第三行和第三列所有元素相似性都置为0,则当前形成下图:

6.发现坐标[2,2]对应的当前最高值小于阈值a,则计算过程结束,输出分子值Total=1.97。此时两个句子各自剩余1个语言片段没有进行匹配,即:“脑多少”和“算计价”,可以将这两个片段看做两个句子语义不同的部分,用来计算分母。
2.分母的计算
语义版Jaccard公式的分母分为两部分:第一部分其实就是分子,代表两个语言片段集合语义相似的部分;第二部分从含义上代表两个语言片段集合语义不同的部分。而这两者之和代表两个集合的语义并集。
假设经过分子计算步骤后,我们已经把参与分子部分计算的语言片段陆续都从SetA和SetB中删除掉,那么两个集合SetA和SetB可能都会剩余部分语言片段没有进行匹配,则分母部分的m定义为:
其含义是两个集合中没有达到语义匹配标准(由阈值a控制)的总片段个数或者两者中取最大值。
Xdif代表SetA中没有参与分子计算的所有语言片段;Ydif代表SetB中没有参与分子计算的所有语言片段。而Cosine(Xdif, Ydif)的意思是两者的语义相似性,所以1-Cosine(Xdif, Ydif)代表两者的语义差异大小,两者语义差异越大则两个句子整个语义版Jaccard相似性分数会被拉低。而m和1-Cosine(Xdif, Ydif)相乘可以这么理解其含义:两个集合有m个片段语义不匹配,而每个不匹配片段的不匹配程度是1-Cosine(Xdif, Ydif),所以可以将其理解为不匹配片段的权重。而语义版Jaccard分子部分也可以理解为语义匹配片段与其权重乘积之和,而其权重则为两个语言片段的语义Cosine相似性。也就是说,这个语义版Jaccard公式的本质是:把两个集合根据阈值a拆分为两个子集合:语义匹配片段子集合/语义不匹配片段子集合;分子部分是语义匹配片段及其权重乘积之和;而分母部分是两个集合的并集,即是分子部分代表的两个集合语义相同部分和由语义不匹配片段子集合计算出的两者语义差异部分。
我们接着把上面没有算完的语义Jaccard计算例子算完,在分子计算部分我们已经算出两者的语义相似性Total=1.97,此时可以算分母了:首先,因为两个句子只剩下“脑多少”和“算计价”两个语义不匹配的片段,所以可以得出m=1,而Cosine(Xdif, Ydif)=0.45,所以1-Cosine(Xdif, Ydif)=0.55,于是m*(1-Cosine(Xdif, Ydif))=0.55,得出分母值为:1.97+0.55=2.52,由于分子部分是1.97,于是这两个句子的语义版Jaccard最终得分为:
SemJac(“电脑多少钱”,” 计算机的价格”)=1.97/2.52=0.78
而对应的原生态Jaccard计算出的相似性分值为0,由此可见,语义版Jaccard确实是可以改善经典Jaccard只做字面匹配的缺点,体现出句子深层次的语义相似性的。
|阈值参数调节方法
如果仔细观察,你会发现语义版Jaccard公式上方游荡着一个面目狰狞的幽灵,一个潜在的不安定因素,就是那个阈值a。因为它鬼魅般的存在,使得我们面临一个尴尬的选择,那就是这个阈值应该取多少是合理的。
虽说我们是ML界的无产阶级,从拥有的训练数据数量角度来说属于一穷二白三没辙,但是就算是解放前万恶的旧社会,过年的时候杨白劳也要想办法给亲闺女扯个红头绳不是。作为ML界的民工,我们也可以自力更生,自己做少量比如几百条训练数据,用这些极少量的训练数据来过个好年。
可以这么着来多快好省地调整出合理的阈值参数:做出一批语义相同的句子对作为正例,然后再做一批语义重叠但是又不同的句子对作为负例。然后不断调整阈值a的取值,优化目标是看哪个阈值能够使得语义Jaccard公式计算出正例的相似度得分整体偏高往上移,而负例的相似度得分整体偏低往下走。这有点类似于机器学习里面通过验证集调整超参数的做法,不过对训练数据数量要求会小得多。
我们从自己做的整个训练集合中抽取子集合,选择大约400对语义相同的句子对作为正例集合,选择大约400对语义相关但是不同的句子对作为负例。然后判断使用不同阈值语义版Jaccard对这些句子对的分值区间分布情况,我们知道无论是原生态Jaccard还是语义版Jaccard,其分值区间都落在[0,1]之间,我们把分值区间再细分为10个子区间:
[0,0.1],[0.1,0.2],[0.2,0.3]……[0.9,1.0] (在后续图示中,纵轴标号为10的为[0,0.1]区间,标号为9的为[0.1,0.2]区间,以此类推)
这样就可以画出不同阈值下正负例得分在10个区间的分布情况,而能够最好地把正负例区分开的阈值就是好阈值。下面分别是阈值a=0.5和a=0.9时的分值分布情况:
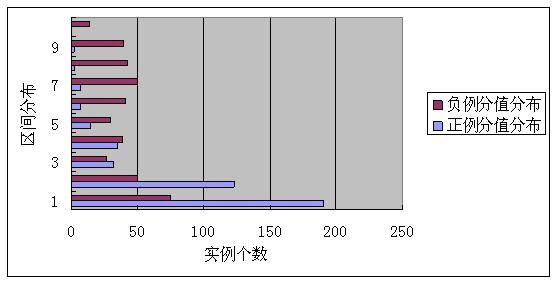
语义版Jaccard正负例分值区间区分度(阈值a=0.5)
语义版 Jaccard 正负例分值区间区分图(阈值 a=0.9 )
从上面两组不同阈值的实验结果可以看出,阈值a=0.9对正负例的区分情况要明显优于a=0.5的情况。通过设置不同的阈值进行实验,我们得出的最优阈值就是0.9,在这个阈值下对正负例句子对的语义区分程度最强。
通过上述方式,我们就可以只利用少数训练数据来获得超参数a的合理取值范围,这就是我们ML界农民工们喜闻乐见的场景。
|语义版Jaccard vs原生态Jaccard实验效果对比
为了验证语义版Jaccard相对原生态Jaccard在句子相似性判断任务上的有效性,我们做了实验对比。实验方法如下:
从整个训练集合中抽取子集合,选择大约400对语义相同的句子对作为正例集合,选择大约400对语义相关但是不同的句子对作为负例。然后判断使用原生态Jaccard及语义版Jaccard对这些句子对的分值区间分布情况。
因为原生态Jaccard没有可调参数,所以只会得出一组分值。而语义版Jaccard我们按照上节介绍的阈值调优方法选择最优参数阈值a=0.9,得出的正负例得分分布情况如下面两图所示:
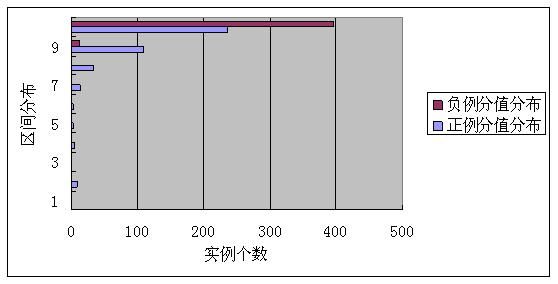
经典Jaccard正负例分值区间区分图
从这张图可以看出,原生态Jaccard公式对于正负例区分度很差,大多数正例和负例得分都落在了[0.0.1]之间,这是由于其只对句子进行字面级别的相似判断导致的。
语义版Jaccard正负例分值区间区分图(a=0.9)
从上面这张图可以看出,语义版Jaccard在进行阈值调优后,可以很明显地把正例和负例语义相似性得分在[0,1]分值区间内散落区分开,正例大多数分值落在[0.4,1.0]区间,负例大多数分值落在[0,0.4]以内,。在这个数据集合下,当阈值a取0.9时,如果把语义Jaccard计算相似性阈值设定为0.4,即给定两个句子<A,B>,利用语义版Jaccard计算公式对其相似性打分,如果得分高于0.4即判断为语义相同,得分低于0.4判断为语义不同,那么其将获得较高的判断准确率,而原生版Jaccard公式因为大多数正例和负例得分都落在[0,0.1]区间,所以很难选择判断标准。当然对于很多应用来说,只需要知道0.9这个阈值即可,不需要确定0.4这个区分标准。
由上述实验结果可知,语义版Jaccard公式可以表达句子深层语义的相似性,而且可以通过少量训练数据获取最具区分度的阈值,所以相信将其作为一个新的计算语义相似性工具箱的工具,会对很多机器学习应用有直接的帮助作用,理论上凡是使用经典Jaccard的计算场景都可以引入语义版Jaccard计算公式。
致谢:感谢畅捷通公司智能平台桑海岩、薛会萍、沈磊、黄通文等同事对于计算实现或训练语料收集方面的工作。当然,考虑到本文的行文风格,也许你们宁愿没有这段指名道姓的致谢。
 扫一扫关注微信号:“布洛卡区” ,深度学习在自然语言处理等智能应用的技术研讨与科普公众号。
扫一扫关注微信号:“布洛卡区” ,深度学习在自然语言处理等智能应用的技术研讨与科普公众号。