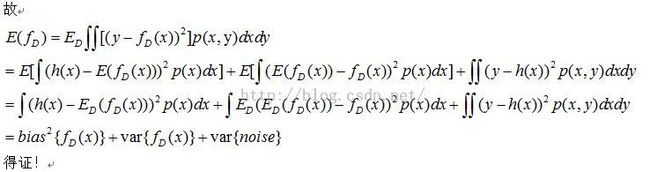偏置方差分解Bias-variance Decomposition
http://blog.csdn.net/pipisorry/article/details/50638749
偏置-方差分解(Bias-Variance Decomposition)
偏置-方差分解(Bias-Variance Decomposition)是统计学派看待模型复杂度的观点。Bias-variance 分解是机器学习中一种重要的分析技术。给定学习目标和训练集规模,它可以把一种学习算法的期望误差分解为三个非负项的和,即本真噪音noise、bias和 variance。
noise 本真噪音是任何学习算法在该学习目标上的期望误差的下界;( 任何方法都克服不了的误差)
bias 度量了某种学习算法的平均估计结果所能逼近学习目标的程度;(独立于训练样本的误差,刻画了匹配的准确性和质量:一个高的偏置意味着一个坏的匹配)
variance 则度量了在面对同样规模的不同训练集时,学习算法的估计结果发生变动的程度。(相关于观测样本的误差,刻画了一个学习算法的精确性和特定性:一个高的方差意味着一个弱的匹配)
假设我们有K个数据集,每个数据集都是从一个分布p(t,x)中独立的抽取出来的(t代表要预测的变量,x代表特征变量)。对于每个数据集D,我们都可以在其基础上根据学习算法来训练出一个模型y(x;D)来。在不同的数据集上进行训练可以得到不同的模型。学习算法的性能是根据在这K个数据集上训练得到的K个模型的平均性能来衡量的,亦即:
其中的h(x)代表生成数据的真实函数,亦即t=h(x)。
我们可以看到,给定学习算法在多个数据集上学到的模型的和真实函数h(x)之间的误差,是由偏置(Bias)和方差(Variance)两部分构成的。
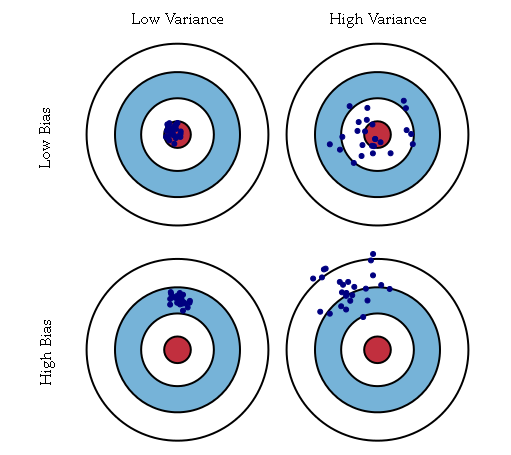
其中偏置描述的是学到的多个模型和真实的函数之间的平均误差,而方差描述的是学到的某个模型和多个模型的平均之间的平均误差(PRML上的原话是variance measures the extent to which the solutions for individual data sets vary around their average)。偏置刻画的是构建的模型和真实模型之间的差异。例如数据集所反映的真实模型为二次模型,但是构建的是线性模型,则该模型的结果总是和真实值结果直接存在差异,这种差异是有构建的模型的不准确所导致的,即为偏置bias;如上图中的下面两个图,真实的模型是红心(即每次都是要瞄准红心的),但是构建的模型是偏离红心的(即在射击时瞄准的是红心偏上方向)。方差刻画的是构建的模型自身的稳定性。例如数据集本身是二次模型,但是构建的是三次模型,对于多个不同的训练集,可以得到多个不同的三次模型,那么对于一个固定的测试点,这多个不同的三次模型得到多个估计值,这些估计值之间的差异即为模型的方差;如上图中的右侧两图,不论构建的模型是否是瞄准红心,每个模型的多次结果之间存在较大的差异。
偏置和方差之间的权衡
所以在进行学习时,就会存在偏置和方差之间的平衡。灵活的模型(次数比较高的多项式)会有比较低的偏置和比较高的方差,而比较严格的模型(比如一次线性回归)就会得到比较高的偏置和比较低的方差。下图形象的说明了以上两种情况:
用于训练的是100个数据集,每个数据集包含25个由h(x)=sin(2πx)[右图中的绿线]随机生成的点的。 参数λ控制模型的灵活性(复杂度),λ越大,模型越简单(严格),反之越复杂(灵活)。我们生成多个模型(左图中的红线),并区多个模型的平均值(右图中的红线)。我们可以看到,当λ较大时(最上面的两个图),平均模型比较简单(最上面的右图),不能很好的拟合真实函数h(x),亦即偏差较大,但是多个模型之间比较相似,差距不大,方差较小(最上面的左图)。当λ较小时(最下面的两个图),平均模型能够非常好的拟合真实函数h(x),亦即偏差较小(最下面的右图),但是多个模型之间差距很大,方差比较大(最下面的左图)。
使用Bagging方法可以有效地降低方差。Bagging是一种再抽样方法(resampling),对训练数据进行有放回的抽样K次,生成K份新的训练数据,在这K个新的训练数据上训练得到K个模型,然后使用K个模型的平均来作为新的模型。随机森林(Random Forest)是一种基于Bagging的强大的算法。
造成偏置和方差的原因除了学习方法的不同和参数的不同(比如λ)之外,数据集本身也会对其造成影响。如果训练数据集和新数据集的分布是不同的,会增大偏置。如果训练数据集过少,会增大方差。
偏置-方差分解是统计学派解释模型复杂度的观点,但是其实用价值不大(Bagging也许是一个例外吧~),因为偏置-方差分解是基于多个数据集的,而实际中只会有一个训练数据集,将这个数据集作为一个整体进行训练会比将其划分成多个固定大小的数据集进行训练再取平均的效果要好。
Bias-variance decomposition推导

Note:ED是对所有数据集D求期望,而不是对x或者y。
from:http://blog.csdn.net/pipisorry/article/details/50638749
ref:Bishop. PRML(Pattern Recognization and Machine Learning). p11-16
Understanding the Bias-Variance Decomposition.
模式识别与机器学习:Bias-Variance分解
偏置方差分解Bias-variance Decomposition
偏置-方差分解(Bias-Variance Decomposition)*
Bias and Variance 偏置和方差*
Andrew NG. CS229 Lecture Note1: Supervised Learning, Discrimitive Algorithms