《数据结构与算法分析》伸展树（自顶向下）详解

前言：

      在完成了自底向上的伸展树之后，我决定把自顶向下的伸展树也做出来。不过这个方式《数据结构与算法分析》书上没讲，完全只能通过自学了。实现的方式比较不容易懂，我在阅读了第二篇博客许多遍之后才明白整个过程。

参考的博客：

 自底向上：

http://www.cnblogs.com/vamei/archive/2013/03/24/2976545.html。我从这一篇博客中学习了不少的新的思想，比如我最开始总想着利用一个函数递归完成插入或者删除操作，却发现其中有一部分的操作不是每个节点都需要的，这个时候可以把删除操作再分出一个子函数来，需要递归的部分由这个子函数完成就行了。这样使得编码简单很多并且易于阅读。

自顶向下：

http://www.cnblogs.com/kernel_hcy/archive/2010/03/17/1688360.html 。这一篇博客写的非常的详细，并且给出了贴图详细讲诉旋转的过程，来源是sedgewick大神的《算法》一书。我根据给出的流程图和伪代码，完全理解之后，用一个小时完成了编码，并且一次测试通过。

我的github：

我实现的代码全部贴在我的github中，欢迎大家去参观。

https://github.com/YinWenAtBIT

介绍：

定义（与上一篇相同）：

         伸展树，或者叫自适应查找树，是一种用于保存有序集合的简单高效的数据结构。伸展树实质上是一个二叉查找树。允许查找，插入，删除，删除最小，删除最大，分割，合并等许多操作，这些操作的时间复杂度为O(logN)。由于伸展树可以适应需求序列，因此他们的性能在实际应用中更优秀。
伸展树支持所有的二叉树操作。伸展树不保证最坏情况下的时间复杂度为O(logN)。伸展树的时间复杂度边界是均摊的。尽管一个单独的操作可能很耗时，但对于一个任意的操作序列，时间复杂度可以保证为O(logN)。
AVLTree的缺点：
1、平衡查找树每个节点都需要保存额外的信息（自底向上的实现方式同样保存了额外信息）。
2、难于实现，因此插入和删除操作复杂度高，且是潜在的错误点。
3、对于简单的输入，性能并没有什么提高。
平衡查找树可以提高性能的地方：
1、平衡查找树在最差、平均和最坏情况下的时间复杂度在本质上是相同的。
2、对一个节点的访问，如果第二次访问的时间小于第一次访问，将是非常好的事情。
3、90-10法则。在实际情况中，90%的访问发生在10%的数据上。
4、处理好那90%的情况就很好了。

自顶向下旋转：

在自底向上的伸展树中，我们需要求一个节点的父节点和祖父节点，因此这种伸展树难以实现或者需要额外的信息。因此，我们可以构建自顶向下的伸展树。
    当我们沿着树向下搜索某个节点X的时候，我们将搜索路径上的节点及其子树移走。我们构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。在伸展操作的过程中：
1、当前节点X是中树的根。
2、左树L保存小于X的节点。
3、右树R保存大于X的节点。
开始时候，X是树T的根，左右树L和R都是空的。和前面的自下而上相同，自上而下也分三种情况：

1、zig情况。

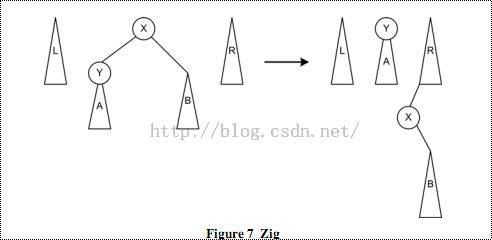
如上图，在搜索到X的时候，要查的节点比X小，并且Y等于要查找的节点（这种方式其实可以合并在zigzag情况之中）。因此Y是下一步要查找的节点，因此Y变成新的中树的树根，X及其右子树被移动到右树上。很显然，右树上的节点都大于所要查找的节点。注意X被放置在右树的最小的位置，即右树最小节点的左孩子指针上。因为X及其子树比原先的右树中所有的节点都要小。这是由于越是在路径前面被移动到右树的节点，其值越大。读者可以分析一下树的结构，原因很简单。

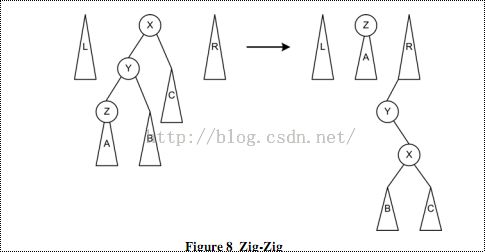
2、zig-zig情况

如图所示：

在这种情况下，所查找的节点在Z的子树中，也就是，所查找的节点比X和Y都小。所以要将X，Y及其右子树都移动到右树中。首先是Y绕X右旋，然后将Z变成新的中树根节点。将Y及其子树移到右树中。注意右树中挂载点的位置。

3、zig-zig情况。
    如图所示：

在这种情况中，先将X及其左子树连接到右树上，然后变成了zag的情况。接下来就可以很轻松的解决了。

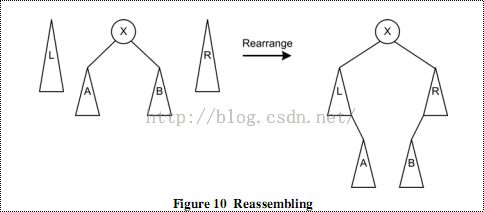
合并：

最后，在查找到节点后，将三棵树合并。如图：]

将中树的左右子树分别连接到左树的右子树和右树的左子树上。将左右树作为X的左右子树。重新最成了一所查找的节点为根的树。

伪代码：

右连接：将当前根及其右子树连接到右树上。左子结点作为新根。
    左连接：将当前根及其左子树连接到左树上。右子结点作为新根。
    T ： 当前的根节点。
Function Top-Down-Splay 
     Do 
          If X 小于 T Then 
               If X 等于 T 的左子结点 Then  
                 右连接 
               ElseIf X 小于 T 的左子结点 Then 
                 T的左子节点绕T右旋 
                 右连接 
               Else X大于 T 的左子结点 Then 
                 右连接 
                 左连接 
               EndIf    
          ElseIf X大于 T Then 
               IF X 等于 T 的右子结点 Then 
                 左连接 
               ElseIf X 大于 T 的右子结点 Then 
                 T的右子节点绕T左旋 
                 左连接 
               Else X小于 T 的右子结点‘ Then 
                 左连接 
                 右连接 
               EndIf 
          EndIf 
     While  ！(找到 X或遇到空节点) 
      组合左中右树 
EndFunction<strong>
</strong>

这个伪代码明显是可以简化的，因为小于根的时候就是右连接，大于根的时候是左连接，其他的情况只不过是先做了别的操作。简化之后如下：

Function Top-Down-Splay
        Do 
              If X 小于 T Then 
                   If X 小于 T 的左孩子 Then 
                     T的左子节点绕T右旋 
                   EndIf    
                右连接 
              Else If X大于 T Then 
                   If X 大于 T 的右孩子 Then 
                     T的右子节点绕T左旋
                   EndIf 
				左连接 
         EndIf

树结构：

自顶向下的操作之后就不再需要父亲节点了，因此可以省下储存空间。

 struct SplayNode
 {
     ElementType Element;
     SplayTree Left;
     SplayTree Right;
 };

 操作：

伸展：

 伸展操作就按照如上的伪代码实现，这次输入的参数改变了，变成了根节点和需要查找的数值。

SplayTree Splay(ElementType X, SplayTree T)
{
	SplayNode pseudo;
	SplayTree ltree, rtree;
	ltree = rtree = &pseudo;
	pseudo.Left = pseudo.Right = NULL;

	if(T == NULL || X == T->Element)
		return T;

	for(;;)
	{
		/*小于中树节点时*/
		if(X < T->Element)
		{
			/*没有左子树则证明没有找到，直接退出*/
			if(T->Left == NULL)
				break;
			/*zigzig形状*/
			if(X < T->Left->Element)
			{
				T = RightSingleRotate(T);
				/*旋转完之后如果没有左节点，一样是没找到*/
				if(T->Left == NULL)
					break;
			}
			/*右连接，把树根节点及右子树连接到右树上*/
			rtree->Left = T;
			rtree = T;
			T = T->Left;
		}
		else if(X > T->Element)
		{
			/*没有右子树则证明没有找到，直接退出*/
			if(T->Right == NULL)
				break;
			/*zagzag形状*/
			if(X > T->Right->Element)
			{
				T = LeftSingleRotate(T);
				/*旋转完之后如果没有右节点，一样是没找到*/
				if(T->Right == NULL)
					break;
			}
			/*左连接，把树根节点及左子树连接到右树上*/
			ltree->Right = T;
			ltree = T;
			T = T->Right;
		}
		/*找到该节点，退出*/
		else
			break;
	}

	/*重新构造树，现在根节点的左右孩子分别接到左树的右节点和右树的左节点*/
	ltree->Right = T->Left;
	rtree->Left = T->Right;
	T->Left = pseudo.Right;
	T->Right = pseudo.Left;

	return T;
}

左旋/右旋：

 左旋右旋的代码与AVLTree的相同。

/*右旋转*/
SplayTree RightSingleRotate(SplayTree T)
{
	SplayTree k1;

	k1 = T->Left;
	T->Left = k1->Right;
	k1->Right = T;
	return k1;
}
/*左旋转*/
SplayTree LeftSingleRotate(SplayTree k1)
{
	Position k2;

	k2 = k1->Right;
	k1->Right = k2->Left;
	k2->Left = k1;
	return k2;
}

最大/小值：

 寻找最大最小值可以通过非递归的方式找到最后一个节点，然后调用Splay函数将该节点变成根节点即可。

 SplayTree FindMin(SplayTree T)
 {
     Position np = T;
     if(T!=NULL)
     {
         while(np->Left !=NULL)
             np = np->Left;

         return Splay(np, T);
     }
     return NULL;
 }

 /*找到最大值之后将该值变为根节点*/
 SplayTree FindMax(SplayTree T)
 {
     Position np = T;
     if(T!=NULL)
     {
         while(np->Right !=NULL)
             np = np->Right;

         return Splay(np, T);
     }
     return NULL;
 }

搜索：

搜索函数现在变得非常简单，直接调用Splay函数，检查返回值是否相等就行。

SplayTree Find(ElementType X, SplayTree T)
{
	/*空树直接返回*/
	if(T==NULL)
	{
		fprintf(stderr, "empty tree");
		return T;
	}
	
	/*不保证最后返回的元素等于X，需要调用者检查*/
	T = Splay(X, T);
	return T;
}

删除：

删除的做法也变得很简单，先调用FInd函数，如果返回的树根不等于要删除的值，那么该值不存在。如果存在，则判断根节点是否同时又左右孩子。如果没有，则可以直接进行删除，新的根节点为其孩子。如果两个孩子都存在，则删除该节点，然后对其左孩子调用FInd函数，查找该值，返回值为左树中的最大值（左树新的根节点没有右孩子）。然后把原来的右孩子连接上即可。

playTree Delete(ElementType X, SplayTree T)
{
	if(T == NULL)
	{
		fprintf(stderr, "empty Tree");
		return T;
	}
	
	T = Splay(X, T);
	if(X == T->Element)
	{
		/*左右子数不为空，那么寻找左子树的最大值作为新的根节点*/
		if(T->Left && T->Right)
		{
			SplayTree ltemp,rtemp;
			ltemp = T->Left;
			rtemp = T->Right;
			free(T);
			ltemp = Splay(X, ltemp);
			ltemp->Right =rtemp;
			T = ltemp;
		}
		/*右子树为空*/
		else if(T->Left)
		{
			SplayTree temp;
			temp = T;
			T = T->Left;
			free(temp);
		}
		/*左子数为空*/
		else
		{
			SplayTree temp;
			temp = T;
			T = T->Right;
			free(temp);
		}
		/*左右子树都为空也没关系，返回的是NULL*/
	}
	else
		printf("%d don't exist", X);

	return T;
}

插入：

插入操作相同，先调用Find函数，如果有要插入的值，则什么也不做。如果没有，则对比要插入的值和根节点值的大小，如果小于根节点，则根节点及其右子树作为新节点的右子数，反之亦然。

/*插入功能实现的方式是先非递归的插入，再进行Splay操作，其实过于复杂，可以优化，
先进行Splay操作，然后再把新值作为根节点和返回的树合并就可以*/
SplayTree insert(ElementType X, SplayTree T)
{
	/*空树时直接创建新的树*/
	if(T == NULL)
	{
		T = (SplayTree)malloc(sizeof(struct SplayNode));
		if(T == NULL)
		{
			fprintf(stderr, "not enough memory");
			exit(1);
		}
		T->Element = X;
		T->Left = T->Right = NULL;
		return T;
	}
	T = Splay(X, T);
	/*元素不存在*/
	if(X != T->Element)
	{
		SplayTree newone;
		newone = (SplayTree)malloc(sizeof(struct SplayNode));
		newone->Element = X;
		/*小于T的根节点，则根节点及其右子树作为新节点的右子数，反之亦然*/
		if(X < T->Element)
		{
			newone ->Right = T;
			newone ->Left = T->Left;
			T->Left = NULL;
		}
		else
		{
			newone ->Left = T;
			newone ->Right = T->Right;
			T->Right = NULL;
		}
		T = newone;
	}

	/*元素存在时直接返回T,与不存在时返回值相同*/
	return T;

}

  

总结：

在实现自顶向下的伸展树时，只用了一个小时就编码完成，并且一次通过了测试代码。原因是我已经在这个树上花了两天的时间，并且在编码之前已经测定弄懂了怎样进行操作。