Decision Tree 及实现

本文基于python逐步实现Decision Tree(决策树)，分为以下几个步骤：

• 加载数据集
• 熵的计算
• 根据最佳分割feature进行数据分割
• 根据最大信息增益选择最佳分割feature
• 递归构建决策树
• 样本分类

关于决策树的理论方面本文几乎不讲，详情请google keywords:“决策树 信息增益  熵”

将分别体现于代码。

本文只建一个.py文件，所有代码都在这个py里

1.加载数据集

我们选用UCI经典Iris为例

Brief of IRIS:

Data Set Characteristics:	Multivariate	Number of Instances:	150	Area:	Life
Attribute Characteristics:	Real	Number of Attributes:	4	Date Donated	1988-07-01
Associated Tasks:	Classification	Missing Values?	No	Number of Web Hits:	533125

Code：

from numpy import *
#load "iris.data" to workspace
traindata = loadtxt("D:\ZJU_Projects\machine learning\ML_Action\Dataset\Iris.data",delimiter = ',',usecols = (0,1,2,3),dtype = float)
trainlabel = loadtxt("D:\ZJU_Projects\machine learning\ML_Action\Dataset\Iris.data",delimiter = ',',usecols = (range(4,5)),dtype = str)
feaname = ["#0","#1","#2","#3"] # feature names of the 4 attributes (features)

Result:

           

左图为实际数据集，四个离散型feature，一个label表示类别（有Iris-setosa, Iris-versicolor，Iris-virginica 三个类）

2. 熵的计算

entropy是香农提出来的（信息论大牛），定义见wiki

注意这里的entropy是H(C|X=xi)而非H(C|X), H（C|X）的计算见第下一个点，还要乘以概率加和

Code：

from math import log
def calentropy(label):
    n = label.size # the number of samples
    #print n
    count = {} #create dictionary "count"
    for curlabel in label:
        if curlabel not in count.keys():
            count[curlabel] = 0
        count[curlabel] += 1
    entropy = 0
    #print count
    for key in count:
        pxi = float(count[key])/n #notice transfering to float first
        entropy -= pxi*log(pxi,2)
    return entropy

#testcode:
#x = calentropy(trainlabel)

Result：

3. 根据最佳分割feature进行数据分割

假定我们已经得到了最佳分割feature，在这里进行分割（最佳feature为splitfea_idx）

第二个函数idx2data是根据splitdata得到的分割数据的两个index集合返回datal (samples less than pivot), datag(samples greater than pivot), labell, labelg。 这里我们根据所选特征的平均值作为pivot

#split the dataset according to label "splitfea_idx"
def splitdata(oridata,splitfea_idx):
    arg = args[splitfea_idx] #get the average over all dimensions
    idx_less = [] #create new list including data with feature less than pivot
    idx_greater = [] #includes entries with feature greater than pivot
    n = len(oridata)
    for idx in range(n):
        d = oridata[idx]
        if d[splitfea_idx] < arg:
            #add the newentry into newdata_less set
            idx_less.append(idx)
        else:
            idx_greater.append(idx)
    return idx_less,idx_greater

#testcode:2
#idx_less,idx_greater = splitdata(traindata,2)


#give the data and labels according to index
def idx2data(oridata,label,splitidx,fea_idx):
    idxl = splitidx[0] #split_less_indices
    idxg = splitidx[1] #split_greater_indices
    datal = []
    datag = []
    labell = []
    labelg = []
    for i in idxl:
        datal.append(append(oridata[i][:fea_idx],oridata[i][fea_idx+1:]))
    for i in idxg:
        datag.append(append(oridata[i][:fea_idx],oridata[i][fea_idx+1:]))
    labell = label[idxl]
    labelg = label[idxg]
    return datal,datag,labell,labelg

这里args是参数，决定分裂节点的阈值（每个参数对应一个feature，大于该值分到>branch，小于该值分到<branch）,我们可以定义如下：

args = mean(traindata,axis = 0)

测试：按特征2进行分类，得到的less和greater set of indices分别为：

也就是按args[2]进行样本集分割，<和>args[2]的branch分别有57和93个样本。

4. 根据最大信息增益选择最佳分割feature

信息增益为代码中的info_gain, 注释中是熵的计算

#select the best branch to split
def choosebest_splitnode(oridata,label):
    n_fea = len(oridata[0])
    n = len(label)
    base_entropy = calentropy(label)
    best_gain = -1
    for fea_i in range(n_fea): #calculate entropy under each splitting feature
        cur_entropy = 0
        idxset_less,idxset_greater = splitdata(oridata,fea_i)
        prob_less = float(len(idxset_less))/n
        prob_greater = float(len(idxset_greater))/n
        
        #entropy(value|X) = \sum{p(xi)*entropy(value|X=xi)}
        cur_entropy += prob_less*calentropy(label[idxset_less])
        cur_entropy += prob_greater * calentropy(label[idxset_greater])
        
        info_gain = base_entropy - cur_entropy #notice gain is before minus after
        if(info_gain>best_gain):
            best_gain = info_gain
            best_idx = fea_i
    return best_idx  

#testcode:
#x = choosebest_splitnode(traindata,trainlabel)

这里的测试针对所有数据，分裂一次选择哪个特征呢？

5. 递归构建决策树

详见code注释，buildtree递归地构建树。

递归终止条件：

①该branch内没有样本（subset为空） or

②分割出的所有样本属于同一类 or 

③由于每次分割消耗一个feature，当没有feature的时候停止递归，返回当前样本集中大多数sample的label

#create the decision tree based on information gain
def buildtree(oridata, label):
    if label.size==0: #if no samples belong to this branch
        return "NULL"
    listlabel = label.tolist()
    #stop when all samples in this subset belongs to one class
    if listlabel.count(label[0])==label.size:
        return label[0]
        
    #return the majority of samples' label in this subset if no extra features avaliable
    if len(feanamecopy)==0:
        cnt = {}
        for cur_l in label:
            if cur_l not in cnt.keys():
                cnt[cur_l] = 0
            cnt[cur_l] += 1
        maxx = -1 
        for keys in cnt:
            if maxx < cnt[keys]:
                maxx = cnt[keys]
                maxkey = keys
        return maxkey
    
    bestsplit_fea = choosebest_splitnode(oridata,label) #get the best splitting feature
    print bestsplit_fea,len(oridata[0])
    cur_feaname = feanamecopy[bestsplit_fea] # add the feature name to dictionary
    print cur_feaname
    nodedict = {cur_feaname:{}} 
    del(feanamecopy[bestsplit_fea]) #delete current feature from feaname
    split_idx = splitdata(oridata,bestsplit_fea) #split_idx: the split index for both less and greater
    data_less,data_greater,label_less,label_greater = idx2data(oridata,label,split_idx,bestsplit_fea)
    
    #build the tree recursively, the left and right tree are the "<" and ">" branch, respectively
    nodedict[cur_feaname]["<"] = buildtree(data_less,label_less)
    nodedict[cur_feaname][">"] = buildtree(data_greater,label_greater)
    return nodedict
    
#testcode:
#mytree = buildtree(traindata,trainlabel)
#print mytree

Result:

mytree就是我们的结果，#1表示当前使用第一个feature做分割，'<'和'>'分别对应less 和 greater的数据。

6. 样本分类

根据构建出的mytree进行分类，递归走分支

#classify a new sample
def classify(mytree,testdata):
    if type(mytree).__name__ != 'dict':
        return mytree
    fea_name = mytree.keys()[0] #get the name of first feature
    fea_idx = feaname.index(fea_name) #the index of feature 'fea_name'
    val = testdata[fea_idx]
    nextbranch = mytree[fea_name]
    
    #judge the current value > or < the pivot (average)
    if val>args[fea_idx]:
        nextbranch = nextbranch[">"]
    else:
        nextbranch = nextbranch["<"]
    return classify(nextbranch,testdata)

#testcode
tt = traindata[0]
x = classify(mytree,tt)
print x

Result：

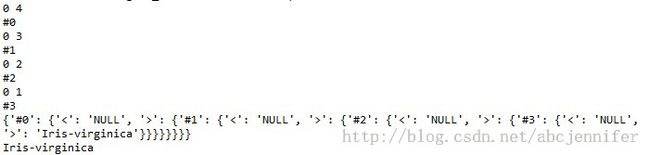
为了验证代码准确性，我们换一下args参数，把它们都设成0（很小）

args = [0,0,0,0]

建树和分类的结果如下：

可见没有小于pivot(0)的项，于是dict中每个<的key对应的value都为空。

本文中全部代码下载：决策树python实现

Reference: Machine Learning in Action

关于Python更多的学习资料将继续更新，敬请关注本博客和新浪微博Rachel Zhang。