菜鸟nginx源码剖析数据结构篇(五) 基数树 ngx_radix_tree_t
菜鸟nginx源码剖析数据结构篇(五) 基数树 ngx_radix_tree_t
Author:Echo Chen(陈斌)
Email:[email protected]
Blog:Blog.csdn.net/chen19870707
Date:October 28h, 2014
1.什么是基数树
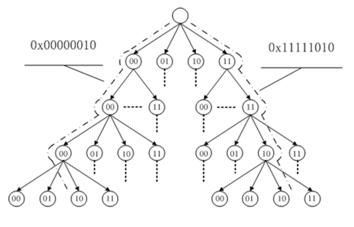
基数树(radix tree)是一种不怎么常见的数据结构,这里简单的做一下介绍:在计算机科学中,基数树,是一种基于trie(字典树)的特殊的数据结构,可以快速定位叶子结点。radix tree是一种多叉搜索树,每个结点有固定的孩子数(叉数 为2^n)。
如下图radix树的分叉为4,树的高度为4,共有4*4*4*4 = 256 个叶子结点,可以快速定位256个结点。
2.ngx_radix_tree_t
ngx_radix_tree 是一种二叉查找树,即叉数为2,它要求存储的每个节点必须以32位整型作为任意两节点的唯一标识,ngx_radix_tree 具备二叉查找树所有优点,并且不用像红黑树通过自身旋转达到平衡,基数树不用管树的形态是否平衡。也因此,它在插入节点、删除节点的速度会比红黑树快的多。
基数树可以不管树平衡的原因在于:红黑树是通过不同节点key关键字的比较决定树的形态,而基数树的每个节点的key关键字自身已经决定了其在树中的位置。先将节点的key关键字转化为二进制,32位,从左至右开始,遇0入左子树,遇1入右子树。
ngx_radix_tree_t树的最大深度为32,由于一般用不到这样的深度,所以引入了掩码,掩码中的1的个数就表示树的高度,掩码1110 0000 0000 0000 0000 0000 0000 0000 ,表示树的高度为3。
eg:如果此时一个节点的key关键字为0x20000000,根据掩码决定取其转化为二进制后的前3位为010,因此,该节点的位置是,根节点-->左子树-->右子树-->左子树。用下图至关表示下:
3.源代码位置
头文件:http://trac.nginx.org/nginx/browser/nginx/src/core/ngx_radix_tree.h
源文件:http://trac.nginx.org/nginx/browser/nginx/src/core/ngx_radix_tree.c
4.数据结构定义
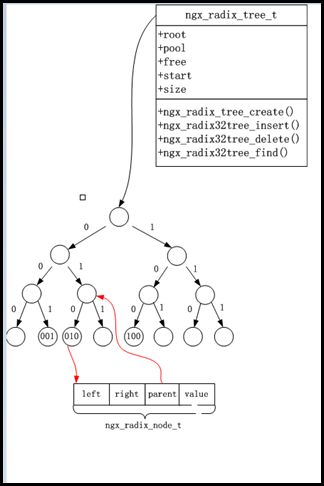
结点中left和right分别指向左右孩子,parent指向父亲结点,value为指向用户自定义的数据的指针。
1: typedef struct ngx_radix_node_s ngx_radix_node_t;
2:
3: struct ngx_radix_node_s {
4: ngx_radix_node_t *right;
5: ngx_radix_node_t *left;
6: ngx_radix_node_t *parent;
7: uintptr_t value;
8: };
与红黑树不同的是,radix_tree自己管理内存,pool为内存池对象,root为根节点,free管理已经分配但暂未使用的节点,free实际上是所有不在树中结点的单链表。start为已分配内存中未使用内存的首地址,size为已分配内存还未使用内存的大小。
1: typedef struct {
2: ngx_radix_node_t *root;
3: ngx_pool_t *pool;
4: ngx_radix_node_t *free;
5: char *start;
6: size_t size;
7: } ngx_radix_tree_t;
5.基数树的创建ngx_radix_tree_create
基数树的构造流程为首先创建 基数树结构 ngx_radix_tree_t ,然后创建 基数树的 root结点,然后根据传入的preallacate参数来决定预分配结点的个数,如果传入-1 ,即按照页面大小决定预分配结点个数,然后就一次插入这些结点。源代码加注释如下:
1: //poll为内存池指针,preallocate是预分配基数树的节点数目,如果传-1,那么将会根据当前系统一个页的大小来预分配基数树结点
2: ngx_radix_tree_t *ngx_radix_tree_create(ngx_pool_t *pool, ngx_int_t preallocate)
3: {
4: uint32_t key, mask, inc;
5: ngx_radix_tree_t *tree;
6:
7: //分配ngx_radix_tree_t
8: tree = ngx_palloc(pool, sizeof(ngx_radix_tree_t));
9: if (tree == NULL) {
10: return NULL;
11: }
12:
13: tree->pool = pool;
14: tree->free = NULL;
15: tree->start = NULL;
16: tree->size = 0;
17:
18: //分配根节点
19: tree->root = ngx_radix_alloc(tree);
20: if (tree->root == NULL) {
21: return NULL;
22: }
23:
24: tree->root->right = NULL;
25: tree->root->left = NULL;
26: tree->root->parent = NULL;
27: tree->root->value = NGX_RADIX_NO_VALUE;
28:
29: //如果需要的预分配结点为0个,完成返回
30: if (preallocate == 0) {
31: return tree;
32: }
33:
34: /*
35: * Preallocation of first nodes : 0, 1, 00, 01, 10, 11, 000, 001, etc.
36: * increases TLB hits even if for first lookup iterations.
37: * On 32-bit platforms the 7 preallocated bits takes continuous 4K,
38: * 8 - 8K, 9 - 16K, etc. On 64-bit platforms the 6 preallocated bits
39: * takes continuous 4K, 7 - 8K, 8 - 16K, etc. There is no sense to
40: * to preallocate more than one page, because further preallocation
41: * distributes the only bit per page. Instead, a random insertion
42: * may distribute several bits per page.
43: *
44: * Thus, by default we preallocate maximum
45: * 6 bits on amd64 (64-bit platform and 4K pages)
46: * 7 bits on i386 (32-bit platform and 4K pages)
47: * 7 bits on sparc64 in 64-bit mode (8K pages)
48: * 8 bits on sparc64 in 32-bit mode (8K pages)
49: */
50:
51: //如果预分配为-1,则按系统的页大小预分配页,以下为根据页面大小,确定preallocate
52: if (preallocate == -1) {
53: switch (ngx_pagesize / sizeof(ngx_radix_node_t)) {
54:
55: /* amd64 */
56: case 128:
57: preallocate = 6;
58: break;
59:
60: /* i386, sparc64 */
61: case 256:
62: preallocate = 7;
63: break;
64:
65: /* sparc64 in 32-bit mode */
66: default:
67: preallocate = 8;
68: }
69: }
70:
71: //inc 的二进制形式为 1000 0000 0000 0000 0000 0000 0000 0000,逐渐向右移动
72: mask = 0;
73: inc = 0x80000000;
74:
75: //依次插入到基数树中
76: while (preallocate--) {
77:
78: key = 0;
79: mask >>= 1;
80: mask |= 0x80000000;
81:
82: //沿途一次插入结点
83: do {
84: if (ngx_radix32tree_insert(tree, key, mask, NGX_RADIX_NO_VALUE)
85: != NGX_OK)
86: {
87: return NULL;
88: }
89:
90: key += inc;
91:
92: } while (key);
93:
94: inc >>= 1;
95: }
96:
97: return tree;
98: }
99:
6.基数树插入操作ngx_radix_tree_insert
基数树的首先遍历树的深度,如果为1,向右子树搜索,否则向左子树搜索,如果找到位置有结点,则直接覆盖。否则,则依次创建沿途结点(0或1)并插入在树中。
1: //tree为基数树,key为关键字,mask为掩码
2: ngx_int_t ngx_radix32tree_insert(ngx_radix_tree_t *tree, uint32_t key, uint32_t mask, uintptr_t value)
3: {
4: uint32_t bit;
5: ngx_radix_node_t *node, *next;
6:
7: bit = 0x80000000;
8:
9: node = tree->root;
10: next = tree->root;
11:
12: //遍历掩码中1的个数,即为树的深度
13: while (bit & mask) {
14: //如果为1,向右子树
15: if (key & bit) {
16: next = node->right;
17: //为0,向左子树
18: } else {
19: next = node->left;
20: }
21:
22: if (next == NULL) {
23: break;
24: }
25:
26: bit >>= 1;
27: node = next;
28: }
29:
30: //这个位置有结点,直接修改值,返回
31: if (next) {
32: if (node->value != NGX_RADIX_NO_VALUE) {
33: return NGX_BUSY;
34: }
35:
36: node->value = value;
37: return NGX_OK;
38: }
39:
40: //如果树中没有结点,依次沿途插入结点
41: while (bit & mask) {
42: next = ngx_radix_alloc(tree);
43: if (next == NULL) {
44: return NGX_ERROR;
45: }
46:
47: next->right = NULL;
48: next->left = NULL;
49: next->parent = node;
50: next->value = NGX_RADIX_NO_VALUE;
51:
52: if (key & bit) {
53: node->right = next;
54:
55: } else {
56: node->left = next;
57: }
58:
59: bit >>= 1;
60: node = next;
61: }
62:
63: node->value = value;
64:
65: return NGX_OK;
66: }
7.基数树删除操作ngx_radix_tree_delete
基数树的删除遍历搜索,遍历基数树的深度(mask中1 个个数),关键字与当前深度为1,向右;否则向左,如果没找到,返回。找到了,并且不为叶子节点,赋值为无效,返回;如果为叶子节点,则将其从基数树中删除,放入空闲链表,并查看其父亲结点是否为一个无效结点,如果也无效,则依次删除。
1: //tree为基数树,key为要删除的结点的关键字,mask为掩码
2: ngx_int_t ngx_radix32tree_delete(ngx_radix_tree_t *tree, uint32_t key, uint32_t mask)
3: {
4: uint32_t bit;
5: ngx_radix_node_t *node;
6:
7: bit = 0x80000000;
8: node = tree->root;
9:
10: //遍历基数树的深度(mask中1 个个数)
11: while (node && (bit & mask)) {
12: //关键字与当前深度为1,向右;否则向左
13: if (key & bit) {
14: node = node->right;
15:
16: } else {
17: node = node->left;
18: }
19:
20: bit >>= 1;
21: }
22:
23: //没找到,返回
24: if (node == NULL) {
25: return NGX_ERROR;
26: }
27:
28: //找到了,并且不为叶子节点,赋值为无效,返回
29: if (node->right || node->left) {
30: if (node->value != NGX_RADIX_NO_VALUE) {
31: node->value = NGX_RADIX_NO_VALUE;
32: return NGX_OK;
33: }
34:
35: return NGX_ERROR;
36: }
37:
38: //为叶子节点
39: for ( ;; ) {
40: //如果在右子树,从树中删除
41: if (node->parent->right == node) {
42: node->parent->right = NULL;
43: //如果在左子树,从树中删除
44: } else {
45: node->parent->left = NULL;
46: }
47:
48: //将该叶子结点链接到空闲链表中
49: node->right = tree->free;
50: tree->free = node;
51:
52: //向上回归,依次删除,直至到不能删除的结点(有有效值的孩子或者自己有有效值)
53: node = node->parent;
54:
55: if (node->right || node->left) {
56: break;
57: }
58:
59: if (node->value != NGX_RADIX_NO_VALUE) {
60: break;
61: }
62:
63: if (node->parent == NULL) {
64: break;
65: }
66: }
67:
68: return NGX_OK;
69: }
8.基数树内存分配ngx_radix_tree_alloc
1: static ngx_radix_node_t *
2: ngx_radix_alloc(ngx_radix_tree_t *tree)
3: {
4: ngx_radix_node_t *p;
5:
6: //如果空闲链表中有结点,取一个返回
7: if (tree->free) {
8: p = tree->free;
9: tree->free = tree->free->right;
10: return p;
11: }
12:
13: //如果空闲链表中没有结点且基数树中的空闲内存大小不够分配一个结点,则从内存池中分配一个页面大小
14: if (tree->size < sizeof(ngx_radix_node_t)) {
15: tree->start = ngx_pmemalign(tree->pool, ngx_pagesize, ngx_pagesize);
16: if (tree->start == NULL) {
17: return NULL;
18: }
19:
20: tree->size = ngx_pagesize;
21: }
22:
23: //从未分配内存中分配,并减小size
24: p = (ngx_radix_node_t *) tree->start;
25: tree->start += sizeof(ngx_radix_node_t);
26: tree->size -= sizeof(ngx_radix_node_t);
27:
28: return p;
29: }
9.基数树查找ngx_radix32tree_find
基数树的查找也很简单,为1向右,为0向左。
1: uintptr_t
2: ngx_radix32tree_find(ngx_radix_tree_t *tree, uint32_t key)
3: {
4: uint32_t bit;
5: uintptr_t value;
6: ngx_radix_node_t *node;
7:
8: bit = 0x80000000;
9: value = NGX_RADIX_NO_VALUE;
10: node = tree->root;
11:
12: while (node) {
13: if (node->value != NGX_RADIX_NO_VALUE) {
14: value = node->value;
15: }
16:
17: if (key & bit) {
18: node = node->right;
19:
20: } else {
21: node = node->left;
22: }
23:
24: bit >>= 1;
25: }
26:
27: return value;
28: }
-
Echo Chen:Blog.csdn.net/chen19870707
-