DeepLearning (三) 预处理:主成分分析与白化
【原创】Liu_LongPo 转载请注明出处
【CSDN】http://blog.csdn.net/llp1992
PCA算法前面在前面的博客中已经有介绍,这里简单在描述一下,更详细的PCA算法请参考我的博客: 机器学习实战ByMatlab(二)PCA算法
PCA 的主要计算步骤
1.数据预处理,使得每一维数据都有相同的均值0
2.计算数据的协方差矩阵, Σ=1m∑mi=1(x(i))(x(i))T
3.对协方差矩阵 Σ 进行奇异值分解,得到特征值 u 以及特征向量 d
4.旋转数据 xrot=UTx
5.选择主成分的个数 k
6.数据降维 x′(i)=x(i)rot,1−k=uT1−kx(i)
PCA 的另外一种解释是: xrot 是一个 n 维向量,其中前 k 个成分可能比较大,而后几个成分可能比较小,PCA 算法做的其实就是丢弃 xrot 后面 n−k 个较小的成分,即将这些成分的值近似为0,然后仅用这前 k 个成分来定义 k 维向量 x′
还原近似数据
当我们得到降维后的数据 x′ , 我们想还原原来的数据,只需要左乘 u 即可,即 x=Uxrot
选择主成分的个数
关于PCA中主成分的个数 k 的选择:
如果 k 过大,则数据压缩率不高,在极限情况 k=n 时,等于是使用原始数据;
如果 k 过小, 则数据的近似误差太大
我们通常考虑的是不同 k 值可以保留的方差百分比,具体来说,如果 k=n ,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果 k=0 ,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
一般而言,设 λ1,λ2,...,λn 表示 Σ 的特征值(由大到小排序,在matlab中可由 svd 函数得到),使得 λj 为对应的特征向量 uj 的特征值,那么如果我们保留前 k 个成分,则保留的方差百分比可计算为:
以处理图像数据为例,一个惯常的经验法则是选择 k 以保留99%的方差,换句话说,我们选取满足以下条件的最小 k 值:
对图像数据应用PCA算法
假设我们的特征为 x1,x2,...,xn ,对于非图像数据的处理,我们一般要计算每个特征 xj 的均值和方差,然后将其取值范围规整化为零均值和单位方差。不过对于大多数自然图像来说,由于其自身的平稳性,图像任一部分的统计性质都应该和其它部分相同,因此我们不用进行方差归一化。
所以对图像进行处理时,步骤如下:
1.求特征均值: u(i):=1n∑nj=1x(i)j
2.零均值处理: x(i)j:=x(i)j−u(i)j for all j
白化
白化其实跟PCA算法还是挺相似的。举例来说,假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:
1.特征之间相关性较低
2.所有特征具有相同的方差(图像处理中我们一般设置为单位方差)
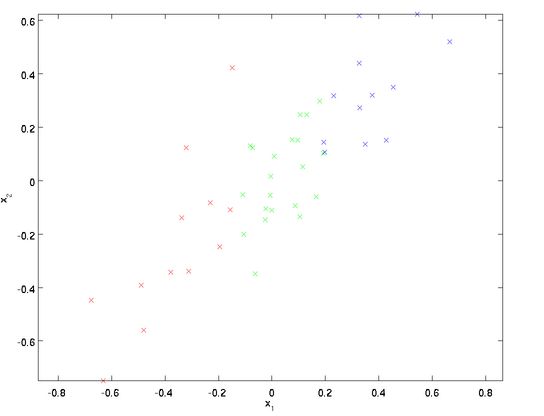
在PCA算法中,我们对数据进行降旋转 x(i)rot=UTx(i) 时,已经消除了输入特征 x(i) 之间的相关性,举个例子:假如我们的二维数据图形化如下:
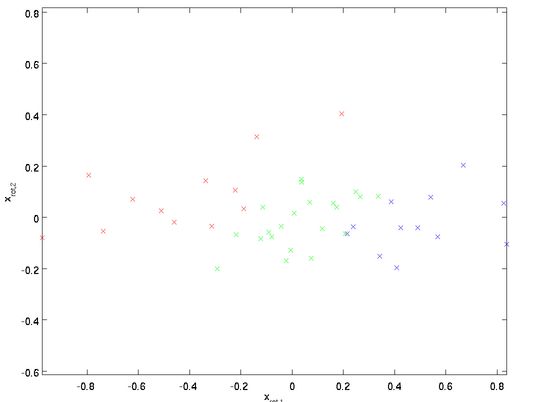
显然这是一个二维数据分布,其中横轴 x1 跟竖轴 x2 之前呈现正相关关系,即 x2 随着 x1 的增大而增大,然后我们将其投影到特征向量上 x(i)rot=UTx(i) ,得到如下图:
此时 x2 已经不随着 x1 的增大而增大了,也就是说 x1 与 x2 消除了相关性。
特征单位方差处理
为了使每个输入特征具有单位方差,我们可以直接使用 1λi√ 作为缩放因子来缩放每个特征 xrot,i ,具体地,我们定义白化后的数据如下:
此时的 xPCAwhite,i 是数据经过PCA白化后的版本, 其不同的特征之间不相关并且具有单位方差。
ZCA 白化
假如 R 是任意正交矩阵,即满足 RRT=RTR=I ,那么 RxPCAwhite 仍然具有单位协方差。在ZCA白化中,令 R=U 。我们定义ZCA白化的结果为:
正则化
实践中需要实现PCA白化或ZCA白化时,有时一些特征值 λi 在数值上接近于0,这样在缩放步骤时我们除以 λ√i 将导致除以一个接近0的值;这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数 ϵ :
当 x 在区间[-1,1]上时, 一般取值为 ϵ≈10−5
对图像来说, 这里加上 ϵ ,对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声,改善学习到的特征。
matlab 实例
1.图像加载 12x12 的patch,共10000个,转换为 144x10000的矩阵,即数据是144维
x = sampleIMAGESRAW();随机显示200个图像块,如下图:
2.零均值化
meanVal = mean(x);
x = bsxfun(@minus,x,meanVal);此时 x 为零均值数据
3.求协方差矩阵,并对协方差矩阵进行奇异值分解,再对数据进行特征向量投影
xRot = zeros(size(x));
[u,d] = svd(x*x'/size(x,2));
xRot = u' * x;4.PCA 检测,计算协方差矩阵
covar = zeros(size(x, 1));
covar = xRot*xRot'/size(xRot,2);此时的协方差矩阵为144x144的矩阵,显示为图像如下:
对角线为数据的自相关,也就是方差,值最大,所以颜色最亮,两边为协方差,值比较小,故颜色较暗,这里为蓝色。
5. 寻找能够保留90%方差的最小 k 值
k = 0;
dVal = diag(d); % 列向量
sumDVal = sum(dVal);
kP = 0;
while kP<0.9
k = k+1;
kP = sum(dVal(1:k)) / sumDVal;
end此时 k 为43,当设置为保留 99% 的方差时, k 为116.
6. PCA降维
xHat = zeros(size(x));
xHat = u(:,1:k) * xRot(1:k,:);将 144维的数据降维到43维,并用43维数据还原图像如下:
7. PCA白化与规则化
epsilon = 0.1;
xPCAWhite = zeros(size(x));
xPCAWhite = bsxfun(@rdivide,xRot,sqrt((dVal+epsilon)));8. 检测PCA白化是否正确,计算协方差矩阵并显示
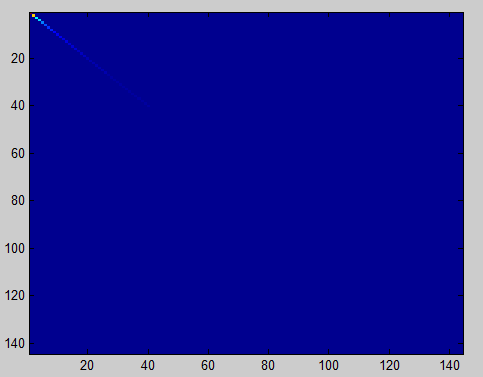
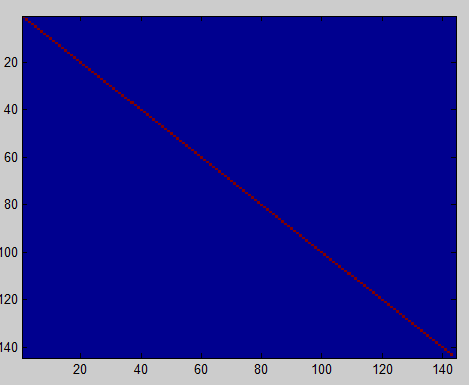
covar = xPCAWhite * xPCAWhite' / size(xPCAWhite,2);白化后的协方差矩阵图像如下:
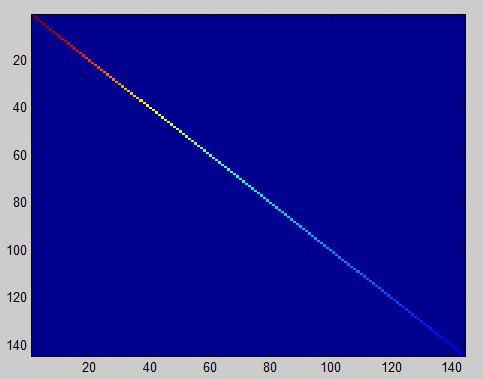
如果没有进行规则化,也就是我们将 ϵ 设置为0,此时白化后的协方差矩阵如下图:
9.ZCA白化
xZCAWhite = zeros(size(x));
xZCAWhite = u*xPCAWhite;ZCA白化后图像如下: