[算法系列之二十五]Ukkonen后缀树算法
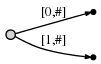
所以我们从左边开始,第一次只插入单字符”a”,通过创建一个从根节点到一个叶节点的边(根节点左边),并且标记这条边[0,#],意思是说这条边代表了从0开始到当前末尾的子串。我使用#来表示当前末尾,当前末尾处在位置1(a的右边)。
因此,我们拥有一棵起始树,图示如下:
![]()
图示意思为:
![]()
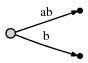
插入单字符”b”。当前末尾位置前进到位置2(b的右边)。 我们每步的目的是就是把所有的前缀都插入到当前位置(Our goal at each step is to insert all suffixes up to the current position. )。通过以下几步完成:
- 扩展已存在边a为ab
- 为b插入一条新边
图示如下:
图示意思为:
我们观察到一下两点:
- 表示ab的那条边与它在起始树时表示一样,都是[0,#]。但它的意义却已经自动发生改变了,因为我们已经#的当前位置从1更改到2了。
- 每条边的空间复杂度都为O(1),因为无论这条边代表多少个字符 ,它都是由指向文本里的两个指针组成(because it consists of only two pointers into the text)。
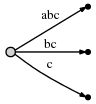
下一步我们再次增加位置,并且修改树,通过给每个已经存在的边增加字符’c’和插入一条表示新后缀c的边。
图示如下:
图示意思为:
我们观察到:
- 这是一棵正确的后缀树。经过以上步骤最终到了达正确位置。(The tree is the correct suffix tree up to the current position after each step)
- 操作步数跟文本中字符数目一样多。(There are as many steps as there are characters in the text)
- 每步的工作量都是O(1),因为所有已经存在的边都是通过增加#来自动修改的。而且为最后一个字符插入一条新边的时间复杂度为 O(1)。因此对一个长度为n的字符串来说,只需要O(n)时间复杂度。(The amount of work in each step is O(1), because all existing edges are updated automatically by incrementing #, and inserting the one new edge for the final character can be done in O(1) time. Hence for a string of length n, only O(n) time is required.)
第一次扩展:简单的重复
当然,这种方法工作的如此良好只是因为我们的字符串中没有包含任何重复字符。现在我们看一个更真实的字符串:
abcabxabcd
这个字符串像前面例子里一样是abc开始的,接着重复ab ,紧跟着x,再接着重复abc,紧跟着d。
步骤1到3:经过前三步后,我们拥有和前面那个例子一样的树:
步骤4:我们移动#到位置4。所有已经存在的边隐含地修改如下:
如之前步骤所言,我们还需要在根节点插入当前步骤的最后一个后缀a。
我们在插入最后一个后缀a之前,我们引入除#之外的两个或者两个更多的变量,当然这些变量一直都存在,只是我们目前为止没有使用它们而已:
- 活动点(active point),它是一个三元组(active_node,active_edge, active_ length)
- 剩余后缀数(remainder),它是一个整数,表名我们还需要插入多少个新的后缀。
这两个变量的含义慢慢的你就会明白,现在我们只能说:
- 在那个简单的abc例子里,活动点总是(root,’0x’,0),也就是说,active_node是根节点,active_edge总是被指定为空字符’0x’,active_ length是0。这么做的结果是我们在每一步插入的那一条新边是作为新创建的边插入到根节点。不久我们就会明白为什么需要三元组表示这些信息。
- 在每步开始时remainder 总是设置为1。这样做的意义是,在每一步结束后我们不得不主动插入的后缀数目为1(总是最后一个字符)。
现在将会发生变化了,当我们给根节点插入当前最后一个字符a的时候,我们注意到已经存在一条以a开始的边:abca。在这种情况下我们做如下工作:
- 我们不会在根节点插入一条新边[4,#]。相反,我们只是注意到后缀a已经在我们的树里。它会终止在更长的边的中间位置,对此我们并不疑惑,我们还是保留它们原来的样子。
- 我们设置活动点为(root,’a’,1)。这意味着活动点现在是在根节点的以a开始的向外的边的中间某个位置,具体地指这条边的位置1之后。我们注意到这条边只是由它的首个字符a来声明的。这就足够了,因为以一个特定的字符开始的只有一条边(通读整个文档之后可以确定这是真的)。
- 我们还增加了remainder, 那么在下一步骤开始的时候,remainder为2。
注意:当发现我们需要插入的最终后缀已经存在在这棵树里的时候,这棵树不会发生任何改变(我们只是修改了活动节点和remainder)。这棵树就不再精确的表示当前位置的后缀树了,但是它已经包含了所有的后缀了(因为最终的后缀a也隐含地包含在里面了)。因此,除了修改变量外(所有这些变量都是定长的,因此空间复杂度是 O(1)),在这一步里没有做其他工作。
步骤5:我们修改#当前的位置为5。这将自动地更新这棵树如下:
而且由于remainder为2 ,我们需要在目前位置需要插入两个最终后缀:ab和b。这主要是因为:
- 在上一步中的后缀a就从来没有真正地插入树中(只是用变量表示而已)。因此它一直保留着,然而由于我们已经向前走了一步,它现在由a变为ab。
- 还有,我们需要插入新的最终边b。
实际上,我们只需要修改活动点(它现在指向的是边abcab中a之后),而且插入当前的最后一个字符b, 不过:同时它也证明b也 已经出现在同一条边里。(But: Again, it turns out that b is also already present on that same edge.)
因此,我们再次不修改这棵树,我们只是:
- 修改活动点为(root,’a’,2)(是与前面相同的节点和边,只不过现在我们指向到b之后)。
- 增加remainder为3,因为我们仍然不能插入前一步里的最终边,同时我们也不能插入当前的最终边。
为了清晰地说明:我们不得不在当前这一步插入ab和b,但是因为ab已经找到,我们只是修改了活动点,甚至都没试图插入b。为什么?因为如果ab处于这棵树里,那么它的每个后缀(包括b)也一定在这棵树里。也许仅仅是隐含性的,不过它一定在这棵树里,因为这是我们迄今为止建立这棵树所采用的方法。
步骤6:我们继续增加#,这棵树自动修改如下:
由于remainder是3 ,我们不得不插入abx,bx和x。活动点告诉我们ab在哪结束,因此我们仅仅需要跳过这儿,然后插入x。x确实还不在这棵树里,因此我们拆分边abcabx,插入一个内部节点:
这条边表示的仍然是指向文本内部的指针,因此拆分和插入内部节点的时间复杂度为O(1)。
这时我们处理了abx,并且把remainder减为2。现在我们需要插入下一个保留的后缀bx。但是在我们做这些之前,我们需要修改活动节点。拆分并插入一条边遵循的规则称作规则1,如下,而且它适用于活动节点是根节点的情况(针对下面后续的其他情况,我们将要了解规则3)。规则1如下:
向根节点插入后,
- active_node 保留为根节点
- active_edge 为我们需要插入的新后缀的第一个字符,也就是 b。
- active_length 减1
因此,新的活动节点三元组为(root,’b’,1)表明下一个插入在bcabx边,第一个字符之后,也就是 b之后。我们可以确定插入点的时间复杂度为 O(1),并且检查x是否已经出现在b之后。如果它出现,我们将结束当前的步骤,保持一切为原样。然而如果x没有出现,那么我们拆分这条边而插入它:
再此说明,它的时间复杂度为 O(1),而且我们按照规则1所示把remainder修改为1,活动节点修改为(root,’x’,0)。
不过还有一件事情需要我们必须做。我们称它为规则2:
如果我们拆分一条边并插入新的节点,如果它不是在当前这一步里创建的第一个节点的话,我们通过特殊的指针,即后缀连接(suffix link),把 以前插入的节点和新增的节点连接起来。后面我们将会知道这么做是有用的。这儿我们要明白:后缀连接用虚线边表示:
我们仍然需要插入当前步骤的最终后缀x。因为活动节点的active_length已经减为0了,因此直接插入到根节点上。由于根节点上没有以x开始的边,所以我们插入了新边:
正如我们所能看到的那样,在当前这一步里插入了所有剩余的后缀。
步骤7: 我们设置#=7,这将像往常一样自动添加下一个字符a到所有的叶子边上。然后我们试图插入新的最终字符到活动节点(根节点),然后发现已经在这棵树里了。因此我们结束当前的步骤,不插入任何边,并且修改活动点为(root,’a’,1)。
步骤8:设置#=8,我们像往常一样添加字符b,这仅仅意味着我们修改活动点为(root,’a’,2) ,增加remainder,其他事情都不需要做。因为b已经出现在这棵树里。然而我们(在 O(1)时间复杂度里)注意到活动节点现在是一条边的结尾(However, we notice (in O(1) time) that the active point is now at the end of an edge. )。我们通过重置活动节点为(node1,’\0x’,0)来反映这个。这儿,我们用node1来指ab边结束的哪个内部节点。
步骤9:接着设置#=9,我们需要插入’c’,这将有助于我们理解的最后一条技巧。
第二次扩展:使用后缀连接(suffix link)
像往常一样,#的修改自动给每条是叶子的边添加了c,而且我们转到活动点看是否可以插入’c’。活动点显示’c’已经存在在那条边里,因此我们设置活动点为(node1,’c’,1),且增加剩余后缀数,不做任何其他事情。
现在 设置#=10进入步骤10,剩余后缀数是4 ,因此我们首先需要在活动点插入d而实现插入abcd(这条边从第三步骤开始就一直保留着)。
试图在活动点插入d将引起时间复杂度为O(1)的边分割:
分割起始的活动点在上图中标记为红色。 最后一条规则即规则3如下:
分割从不是根节点的活动点开始的边之后,我们应当紧跟着从活动点开始的后缀连接,如果存在一条这样的连接,那么重置活动节点使它指向这个节点。如果不存在这样后缀连接,那么我们设置活动节点为根节点,活动边和活动长度保持不变。
因此活动节点现在是(node2,’c’,1),这里node2如下图所示标记为红色:
由于abcd的插入已经完成,我们把剩余后缀数减为3,而且考虑当前步骤的下一个剩余后缀bcd。规则3已经设置活动点为右边的节点和边,因此插入bcd可以简单地向活动点插入剩余后缀的最后一个字符d来完成。要做到这个将引起另一个边分割,根据规则2 ,我们必须创建一条从以前已插入的节点开始的到新建节点的后缀连接:
我们注意到:后缀连接使我们重置了活动点,因为我们能在O(1)复杂度下插入下一个剩余后缀。看看上面的图就可确定标签为ab的真正节点连接到节点b(它的后缀),而节点abc则连接到bc节点。
当前步骤仍然没有结束。现在剩余后缀数是2,我们需要遵循规则3再次重置活动节点。由于当前的活动节点(上图中红色标记的)已经没有后缀连接,我们重置活动节点位根节点。活动节点现在是(root,’c’,1)。
因此下一个插入发生在根节点的一条边上,以c开始的这条边的标签为:cabxabcd,位于第一个字符之后,即c之后。这将产生另一个分割:
另外,由于这涉及到新的内部节点的创建,我们遵循规则2,设置一条新的从前面已创建的内部节点开始的后缀连接:
(为了制作这些小图,我使用了Graphviz Dot软件。新的后缀连接使得Dot软件爱你重新布局了已经存在的边,因此仔细地检查并确定上图中插入的唯一的东西就是一条新的后缀连接。)创建了这条连接,剩余后缀树可设置为1 ,另外由于活动节点是根节点,我们根据规则1修改活动点位(root,’d’,0)。这意味着这一步的最后一个插入是向根节点插入单独的d:
这是最后一步,至此我们已经完成了后缀树的建立。虽然工作已经完成,但还有许多最后要注意的地方:
- 在每一步里,我们向前移动#一个位置。这自动在时间复杂度O(1)内修改了所有的叶子结点。
- 不过,后缀树没有处理 a) 前一步骤保留下来的任何后缀 b)和当前步骤的最后一个字符。
- 剩余后缀树告诉我们我们需要做多少个后续的插入。这些插入把一对一对应为在当前位置#结束的字符串的最后的后缀。我们认为是一个接着一个,然后再对它们进行插入。重要的是:每条插入都在O(1)的时间复杂度内完成,因为活动点告诉我们确切的位置,然后我们只需要在活动点增加一个单独的字符。为什 么?因为其他字符都隐含地包含了(否则活动点将是其他地方)。
- 在做了每个这样的插入之后,我们把剩余后缀数减少,并且如果存在后缀的边,就添加一条后缀连接。如果不存在,(根据规则3)我们把活动节点设置为根节点。如果我们已经处在根节点,那么我们根据规则1修改活动节点。在任何情况下,它只花费O(1)的时间复杂度。
- 在任意插入期间,我们发现我们需要插入的字符已经存在,那么我们不作任何事情而结束当前步骤,甚至在剩余后缀树大于0的情况下。理由是保留的任何插入都是我们试图插入的边的后缀。因此它们所有都隐藏在当前的树里。事实是剩余后缀树大于0确保我们后续对剩余后缀的处理。
- 如果在算法结束时剩余后缀数大于0意味着什么呢?将是这中情况:结束的文本是以前出现在某个地方的这个文本的子字符串。在这种 情况下,我们必须给这个字符串结尾添加一个额外以前没有出现过的字符。在这样的文档里,通常使用美元符号$作为解决这个问题的 符号。为什么会发生这种事情呢?—>如果后来我们使用完整的后缀树搜寻后缀,那么我们只有在后缀结束于叶子时才接受搜寻匹配。 否则我们会得到许多假的匹配,因为后缀树立简单地包含了不是猪字符串的真正后缀的许多这样的字符串。在结束的时候强制剩余后 缀数为0是确保所有的后缀都结束在叶子节点的重要方法。然而,如果玩么想用这棵树来寻找通常的子字符串,而不仅仅是主字符串的 后缀,那么根据下面OP的评论的建议,最后一步确实不是必需的。
- 那么,整个算法的复杂性如何呢?如果文本是长度为n的字符组成,那么显然需要n步(或者如果我们增加了没有符号,那么就是n+1 步)。在每个步骤里,我们要么(除了修改变量外)什么都不做,要门我们插入剩余的后缀,每一步都花费O(1)时间复杂度。由于剩余后缀数表明了我们在以前的步骤里不做任何事情的次数,而且现在我们每做一次插入就对剩余后缀数递减,我们做这样的事情 总的次数准确地说是n(或者n+1)。因此,整体的复杂度是O(n)。
- 然而,有一处小的地方我没有正确地说明: 可能发生这样的情况,我们添加了一条后缀连接,修改活动点,然后发现活动点的活动长度与新的活动节点不能一起正常工作。例如,看看下面这种情况:
![[算法系列之二十五]Ukkonen后缀树算法_第15张图片](http://img.e-com-net.com/image/info5/9cc5e5044d214f05a4f2bab234e42478.jpg)
(短划线指的是这棵树的剩余部分,虚线指的是后缀连接。)
现在,假设活动节点是(red,’d’,3),因此它指向def边的f之后的位置。现在假设我们做了必须的修改,而且现在依据规则3续接了后缀连接并修改了活动节点。新的活动节点是(green,’d’,3)。然而从绿色节点出发的d边是de,因此这条边只有2个字符。为了找到正确的活动点,很明显我们需要添加一个到蓝色节点的边,然后重置活动节点为(blue,’f’,1)。
在特别糟的情况下,活动长度可以是剩余后缀数那么大,它甚至可以与n一样大。再在找正确的活动节点的时候,这种情况可能刚好发生,我们不仅仅需要跳过一个内部节点长度,不过也许很长,最坏的情况是高达n。由于在每一步里 剩余后缀的插入通常是O(n),续接了后缀之后的对活动节点的后续调整也是O(n)的复杂度 ,这是否意味着这个算法具有隐藏的O(n 2)的复杂度?
不是这样的,理由是如果我们确实需要调整活动节点(例如,如上图所示从绿色节点调整到蓝色节点),那么这就给我们引入了一个拥有自己的后缀连接的新节点,而且活动长度将缩减。当我们沿着后缀连接这个链向下走,我们就要插入剩余的后缀,且只是缩减活动长度,使用这种方法我们可以调整的活动点的数目不可能超过任何给定时刻的活动长度。由于活动长度从来不会超过剩余后缀数,而后缀剩余数不仅仅在每个单一步骤里是O(n),而且对整个处理过程进行的剩余后缀递增的总数也是O(n),因此调整活动节点的数目也是以O(n)为界的。
资料:
Ukkonen’s paper on the algorithm
Fast String Searching With Suffix Trees
Ukkonen’s suffix tree algorithm
![[算法系列之二十五]Ukkonen后缀树算法_第1张图片](http://img.e-com-net.com/image/info5/faff096cd0db4a30947859a233498a07.jpg)

![[算法系列之二十五]Ukkonen后缀树算法_第2张图片](http://img.e-com-net.com/image/info5/2912fc4d387a4f5e92d31b2067b92bd4.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第3张图片](http://img.e-com-net.com/image/info5/5a8dcb3a2d8442dfb1d7889de53333da.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第4张图片](http://img.e-com-net.com/image/info5/063abccbbbbf454a955822b41041971c.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第5张图片](http://img.e-com-net.com/image/info5/b3e75f0488364497872eca1d5bb2ec4c.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第6张图片](http://img.e-com-net.com/image/info5/473f48e62da042ffa1980fa3ee1dc1dc.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第7张图片](http://img.e-com-net.com/image/info5/5c69cb7d68de4fdb85276e4f2c39bb5d.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第8张图片](http://img.e-com-net.com/image/info5/a54a689f30b341abbc831387a7b688cb.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第9张图片](http://img.e-com-net.com/image/info5/f2e94195e01e4c559abf9a6ee93f53a9.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第10张图片](http://img.e-com-net.com/image/info5/e829b3f013ab44f6bd95e11415d9f9b0.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第11张图片](http://img.e-com-net.com/image/info5/e81607d89d3948019e3bb5569ac59140.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第12张图片](http://img.e-com-net.com/image/info5/a7bae1058967411ab8a3dce6df109ab2.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第13张图片](http://img.e-com-net.com/image/info5/e1761dc6d7594ac088f48e3dbf2eaa77.jpg)
![[算法系列之二十五]Ukkonen后缀树算法_第14张图片](http://img.e-com-net.com/image/info5/9a1b3d0463bc469d90900a3ee5a42b29.jpg)