压缩感知中的数学知识:线性方程组的解
转自彬彬有礼的专栏http://blog.csdn.net/jbb0523/article/details/41577721
题目:压缩感知中的数学知识:线性方程组的解
====================引言====================
有关“线性方程组的解”这个问题实在是太基础的一个线性代数问题,本也不想去讨论它,但近几天看麻省理工GilbertStrang的线性代数公开课,有些感触,就写写吧,因为我确实也搞不清楚“线性方程组的解”这个问题,可能当年上学时知道,但现在的确已经忘的干干净净了,而且翻了几次线性代数的书也没有坚持好好看下去,还是有些浮躁吧。
具体内容可看麻省理工GilbertStrang的线性代数公开课第7讲和第8讲,推荐在暴风影音中看,因为那里的画面质量比其它网站的要高一些。
====================正文====================
一、研究对象

二、“线性方程组的解”总结
首先把结论把在这里,算是一个备忘吧,可以随时备查:
若矩阵A的秩为r,即r=R(A) :
1)若r=M=N,则线性方程组Ax=b有唯一解;
2)若r=N<M,则线性方程组Ax=b有唯一解或无解;
3)若r=M<N,则线性方程组Ax=b有无穷解;
4)若r<M, r<N,则线性方程组Ax =b有无穷解或无解;
三、针对总结的举例分析
1、若r=M=N,则线性方程组Ax=b有唯一解
这是最初级的情况,N个未知数,N个独立的方程,大家从书上第一次学解方程组就是这类情况了。例如:
2、若r=N<M,则线性方程组Ax=b有唯一解或无解
这种情况下由于N<M,即未知数个数小于方程个数,因此很可能导致无解,例如:

但在特殊情况下也会有唯一解:
这是因为第二个方程和最后一个方程实际上是等价的。更复杂一点的有唯一解的例子:
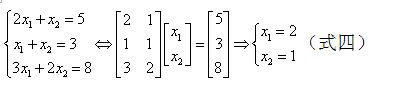
这是因为第三个方程是就是第一个方程加上第二个方程。
3、若r=M<N,则线性方程组Ax=b有无穷解
这种情况下由于M<N,即未知数个数大于方程个数,因此有若干未知数是自由存在的,例如:
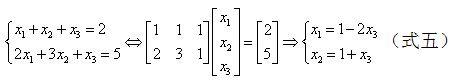
即只能推导出待求未知数x1,x2,x3之间的关系,其中一个可任意取值。当然如果按照线性代数的写法则为:

4、若r<M, r<N,则线性方程组Ax =b有无穷解或无解

四、四种情况在向量空间的解释
其实以上四种情况都可以从向量空间的角度去理解:
对Ax =b,若b在A的列空间C(A)中则方程组有解,若M=N且b在A的列空间C(A)中则有唯一解,若b不在A的列空间C(A)中则方程组无解。(可以这样理解A的列空间C(A):矩阵A的所有列向量的线性组合组成的空间或者说轨迹,即矩阵A的所有列向量的生成子空间)
对于式一:矩阵A的列空间C(A)为整个平面R2且矩阵A只有两个列向量,向量b是一个二维列向量,所以一定在平面R2上,故有唯一解;
对于式二:矩阵A的列空间C(A)为立体空间R3中的某一个平面P,而向量b=[5 3 1]T不在这个平面P内,故无解;
对于式三和式四:矩阵A的列空间C(A)分别为立体空间R3中的某一个平面P,而b=[5 3 6]T和b=[5 3 8]T分别在自己对应的矩阵A的列空间平面P内,故有唯一解;(矩阵A有两个列向量且不在一条直线上,所以它们确定一个平面P,并且此平面P中的任意向量由两个列向量唯一线性组合表示)
对于式五:矩阵A的列空间C(A)为整个平面R2(因为每个列向量都是二维的),而对于一个平面只需要此平面上两个不在一条直线上的向量即可唯一确定,矩阵A有三个列向量,所以有一个是冗余的,故有无穷多解;
对于第四种情况中有无穷解的方程组,虽然矩阵A有三个三维的列向量,但它们其中一个可以由另外两个表示,比如第三列等于两倍的第一列再减去第二列,即矩阵A的列空间C(A)为一个平面P,而向量b恰好在这个平面P内,类似于前面有无穷多解的分析,此时有无穷解;而对于无解的方程组,矩阵A的三个列向量实际上为同一向量,即它们在同一条直线上,因此矩阵A的列空间C(A)为一条直线,而向量b却不在这条直线上,故无解。
五、向量空间与线性组合的等价
以上四种情况的另一个等价描述是A的列的线性组合能否表示b,若有能表示则有解,若能唯一表示则有唯一解,若不能表示则无解,b能否由A的列的线性组合表示实际上就是向量b是否在矩阵A的列空间C(A)中。
六、应用
压缩感知就是对一个N维信号x进行一个压缩观测得到M个观测值y,即y=Φx,其中M<<N,然后由压缩观测y恢复信号x的过程;所以压缩感知属于第三种情况,此类方程我们称为病态方程或欠定方程,英文一般写为ill-posed。
为了求解欠定方程y=Φx,我们将信号在某组稀疏基Ψi,i=1~N,下进行展开,即x=Ψθ,稀疏矩阵Ψ为N×N维,展开系数θ为N×1维的列向量且是K稀疏的,即只有K项非零项且K<<N,则观测方程y=Φx变为y=ΦΨθ,令A=ΦΨ,则y=ΦΨθ表示为y=Aθ,虽然此时方程y=Aθ仍为欠定方程,但由于展开系数θ是K稀疏的,因此可以通过某种数学方法由压缩观测y恢复稀疏展开系统θ,然后由x=Ψθ即可得到信号x。
额外说一下,第二种r=N<M的情况也是很常见的(无解情况),比如在卫星导航定位时就是要对此类方程求得一个最小二乘解即我们的位置。

