ACM-计算几何之Cows——poj3348
Cows
Description
Your friend to the south is interested in building fences and turning plowshares into swords. In order to help with his overseas adventure, they are forced to save money on buying fence posts by using trees as fence posts wherever possible. Given the locations of some trees, you are to help farmers try to create the largest pasture that is possible. Not all the trees will need to be used.
However, because you will oversee the construction of the pasture yourself, all the farmers want to know is how many cows they can put in the pasture. It is well known that a cow needs at least 50 square metres of pasture to survive.
Input
The first line of input contains a single integer, n (1 ≤ n ≤ 10000), containing the number of trees that grow on the available land. The next n lines contain the integer coordinates of each tree given as two integers x and y separated by one space (where -1000 ≤ x, y ≤ 1000). The integer coordinates correlate exactly to distance in metres (e.g., the distance between coordinate (10; 11) and (11; 11) is one metre).
Output
You are to output a single integer value, the number of cows that can survive on the largest field you can construct using the available trees.
Sample Input
4
0 0
0 101
75 0
题目:http://poj.org/problem?id=3348
Time Limit: 2000MS Memory Limit: 65536K
Total Submissions: 6245 Accepted: 2850Description
Your friend to the south is interested in building fences and turning plowshares into swords. In order to help with his overseas adventure, they are forced to save money on buying fence posts by using trees as fence posts wherever possible. Given the locations of some trees, you are to help farmers try to create the largest pasture that is possible. Not all the trees will need to be used.
However, because you will oversee the construction of the pasture yourself, all the farmers want to know is how many cows they can put in the pasture. It is well known that a cow needs at least 50 square metres of pasture to survive.
Input
The first line of input contains a single integer, n (1 ≤ n ≤ 10000), containing the number of trees that grow on the available land. The next n lines contain the integer coordinates of each tree given as two integers x and y separated by one space (where -1000 ≤ x, y ≤ 1000). The integer coordinates correlate exactly to distance in metres (e.g., the distance between coordinate (10; 11) and (11; 11) is one metre).
Output
You are to output a single integer value, the number of cows that can survive on the largest field you can construct using the available trees.
Sample Input
4
0 0
0 101
75 0
75 101
151
这道题,计算几何,恩,求凸包的面积。
题意就是,这个人要在森林中把几棵树围起来养牛,一只牛占地50,
给你一些树的坐标问,最多养多少头牛。
就是,求凸包面积,然后除以50.。。。
这道题有一点,那个面积用整型存储,浮点类型存储会WA。。。
代码,就是贴求凸包的模板(Graham算法)
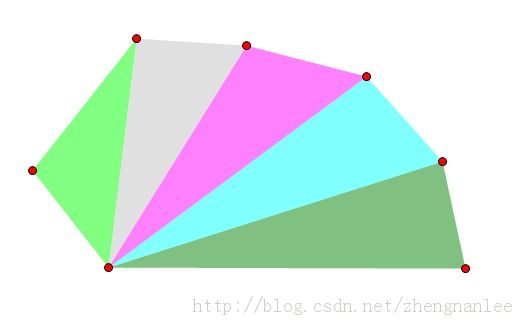
然后,根据凸包数组,求一个个三角形面积。
三角形面积,就是叉积的一半,叉积求的是平行四边形面积。
/*
Author:Tree
From: http://blog.csdn.net/lttree
Cows
poj 3348
凸包面积
*/
#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
struct point
{
double x,y;
}pnt[10001],res[10001];
// 两向量叉积
double cross( point sp,point ep,point op)
{
return (sp.x-op.x)*(ep.y-op.y)-(ep.x-op.x)*(sp.y-op.y);
}
// sort数组排序,比较的<号重载
bool operator < (const point &l,const point &r)
{
return l.y<r.y || (l.y==r.y && l.x<r.x) ;
}
int Graham( int n )
{
int i,len,top=1;
// 先对所有点按照极角排序
// 纵坐标最小的排在前面,纵坐标相同,横坐标小的排在前面
sort(pnt,pnt+n);
// 判断点的个数是否大于2(所给的点能否构成凸包)
if( n==0 ) return 0;res[0] = pnt[0];
if( n==1 ) return 1;res[1] = pnt[1];
if( n==2 ) return 2;res[2] = pnt[2];
// 用叉积来判断后面的点是否为凸包中的点
for( i=2;i<n;++i )
{
while( top && cross(pnt[i],res[top],res[top-1])>=0 ) top--;
res[++top] = pnt[i];
}
len = top; res[++top] = pnt[n-2];
// 判断最后三个点
for(i=n-3;i>=0;--i)
{
while( top!=len && cross(pnt[i],res[top],res[top-1])>=0 ) top--;
res[++top] = pnt[i];
}
return top;
}
int main()
{
int n,i,len;
int area;
while(scanf("%d",&n)!=EOF && n)
{
for(i=0;i<n;++i)
scanf("%lf%lf",&pnt[i].x,&pnt[i].y);
// len为凸包数组内点的个数
len=Graham(n);
// 判断n为0,1,2的情况(无法构造凸包的情况)
if(len<3) {printf("0\n");continue;}
// 求面积
area=0;
for(i=1;i<len-1;++i)
area= area + fabs(cross(res[i],res[i+1],res[0])/2.0);
printf("%d\n",area/50);
}
return 0;
}