《数据结构与算法分析》图论算法--邻接表与拓扑排序
前言:
上一周一直在忙着准备阿里巴巴的笔试,花了大量时间复习以前的内容,不过感觉好像没有起到什么作用![]() ,现在不想这些问题了,先专心学习数据结构。现在终于来到了本科时遇到最头疼的图论了。本科时就只会在纸上画一画算法,现在我要亲手实现它们。
,现在不想这些问题了,先专心学习数据结构。现在终于来到了本科时遇到最头疼的图论了。本科时就只会在纸上画一画算法,现在我要亲手实现它们。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
图论算法:
若干定义:
一、图的概念
简单讲,一个图是由一些点和这些点之间的连线组成的。严格意义讲,图是一种数据结构,定义为:graph=(V,E),V是点(称为“顶点”)的非空有限集合,E是线(称为“边”)的集合,边一般用(vx,vy)表示,其中vx,vy属于V。
二、无向图和有向图
如果边是没有方向的,称此图为“无向图”,用一对圆括号表示无向边,显然(vx,vy)和(vy,vx)是两条等价的边,
如果边是有方向(带箭头)的,则称此图为“有向图”,用一对尖括号表示有向边,边<v1,v2>。把边<Vx,Vy>中Vx称为起点,Vy称为终点。显然此时边<vx,vy>与边<vy,vx>是不同的两条边。有向图中的边又称为弧,起点称为弧头,终点称为弧尾。
一个图可以表示为:V={v1,v2,v3},E={<v1,v2>,<v1,v3>,<v2,v3>,<v3,v2>} 如果两个顶点U、V之间有一条边相连,则称U、V这两个顶点是关联的。
三、带权图
一个图中的两顶点间不仅是关联的,而且在边上还标明了数量关系,这种数量关系可能是距离、费用、时间、电阻等等,这些数值称为相应边的权。边上带有权的图称为带权图,也称为网(络)。
四、阶
图中顶点的个数称为图的阶。
五、度
图中与某个顶点相关联的边的数目,称为该顶点的度。度为奇数的顶点称为奇点,度为偶数的顶点称为偶点。
在有向图中,把以顶点V为终点的边的数目称为顶点V的入度,把以顶点U为起点的边的数目称为顶点U的出度,出度为0的顶点称为终端顶点。
定理1:无向图中所有顶点的度之和等于边数的2倍,有向图中的所有顶点的入度之和等于所有顶点的出度之和。
定理2:任意一个无向图一定有偶数个(或0个)奇点。
六、完全图
若无向图中的任意两个顶点之间都存在着一条边,有向图中的任意两个顶点之间都存在着方向相反的两条边,则称此图为完全图。n阶完全有向图含有n*(n-1)条边,n阶完全无向图含有 n*(n-1)/2条边,当一个图接近完全图时,称为稠密图;相反,当一个图的边很少时,称为稀疏图。
七、子图
设有两个图G =(V,E)和G’=(V’,E’),若V’是V的子集,E’是E的子集,则称G’为G的子图。
八、路(径)
在一个G =(V,E)的图中,从顶点v到顶点v’的一条路径是一个顶点序列vi0,vi1,vi2,vi3, vim,其中 vi0 = v, vim = v’,若此图是无向图,则(vij-1,vij)∈E,1≤j≤m;若此图是有向图,则<vij-1,vij>∈E,1≤j≤m。路径长度是指路径上的边或弧的数目。序列中顶点不重复出现的路径称为简单路径,顶点v和顶点v’相同的路径称为回路(或环)。除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路(或简单环)。
九、连通图
在无向图G中,如果从顶点U到顶点V有路径,则称U和V是连通的。如果对于图G中的任意两个顶点U和V都是连通的,则称图G是连通图,否则称为非连通图。
在有向图G中,如果对于任意两个顶点U和V,从U到V和从V到U都存在路径,则称图G是强连通图。
图的存储结构:
一、邻接矩阵表示法
邻接矩阵是表示顶点之间相邻关系的矩阵,设G={V,E}是一个度为n的图(顶点序号分别用1,2,3,n表示),则G的邻接矩阵是一个n阶方阵,G[i,j]的值定义如下:
当vi与vj之间有边或弧时,取值为1或权值
G[ i,或∝ 当vi与vj之间无边或弧时,取值为0或∝(无穷大)。
采用邻接矩阵表示图,直观方便,很容易查找图中任两个顶点i和j之间有无边(或弧),以及边上的权值,只要看A[i,j]的值即可,因为可以根据i,j的值随机查找存取,所以时间复杂性为O(1)。也很容易计算一个顶点的度(或入度、出度)和邻接点,其时间复杂性均为O(n)。但是,邻接矩阵表示法的空间复杂性为O(n*n),如果用来表示稀疏图,则会造成很大的空间浪费。
二、边集数组表示法
边集数组是利用一维数组存储图中所有边的一种图的表示方法。每个数组元素存储一条边的起点、终点和权值(如果有的话)。在边集数组中查找一条边或一个顶点的度都需要扫描整个数组,所以其时间复杂性为O(e),e为边数。这种表示方法适合那些对边依次进行处理的运算,而不适合对顶点的运算和对任意一条边的运算。从空间复杂性上讲,边集数组适合于存储稀疏图。
三、邻接表表示法(链式存储法)
邻接表表示法是指对图中的每个顶点vi(1≤i≤n)建立一个邻接关系的单链表,并把它们的表头指针用一维向量数组存储起来的一种图的表示方法。为每个顶点vi(1≤i≤n)建立的单链表,是表示以该顶点为起点的所有边的信息(包括一个终点(邻接点)序号、一个权值和一个链接域)。一维向量数组除了存储每个顶点的表头指针外,还要存储该顶点的编号i。
图的邻接表表示法便于查找任一顶点的关联边及邻接点,只要从表头向量中取出对应的表头指针,然后进行查找即可。由于无向图的每个顶点的单链表平均长度为2e/n,所以查找运算的时间复杂性为O(e/n)。对于有向图来说,想要查找一个顶点的后继顶点和以该顶点为起点的边、包括求该顶点的出度都很容易;但要查找一个顶点的前驱顶点和以此顶点为终点的边、以及该顶点的入度就不方便了,需要扫描整个表,时间复杂度为O(n+e)。所以,对于经常查找顶点入度或以该顶点为终点的关联边的运算时,可以建立一个逆邻接表,该表中每个顶点的单链表存储的是所有以该点为终点的关联边信息。甚至还可以把邻接表和逆邻接表结合起来,构造出“十字邻接表”,此时,每个边结点的数据信息包含五个域:起点、终点、权、以该顶点为终点的关联边的链接、以该顶点为起点的关联边的链接。表头向量的结点也包括三个域:顶点编号、以该点为终点的表头指针域、以该点为起点的表头指针域。
代码实现:1、邻接表表示图:
我在这里使用的是哈希表来完成的顶点的名字到顶点的编号。在选择处理冲突的方式的时候,最开始我没想明白邻接表,居然使用了分离链接法。写到一半就发现不对了,这样做没法让一个编号对应一个顶点。然后第二次编写的时候,改成了开放定址法。将哈希表中每一个节点设置为了顶点节点,顶点节点再指向边节点。数据结构定义如下:
/*令Empty默认为0,则使用calloc可以自动初始化为Empty*/
enum KindOfEntry
{
Empty =0,
Legitimate,
Deleted
};
struct EdgeNode
{
int vertexIndex;
WeightType weight;
Edge next;
};
struct VertexNode
{
VertexType vertexName;
int vertexIndex;
Edge next;
enum KindOfEntry Info;
};
typedef struct VertexNode Cell;
struct HashTbl
{
int TableSize;
int vertex, edge;
Cell * TheCells;
};
在这里我的实现实际上是有问题的,实际上哈希表应该只容纳顶点个数V个成员,但是在这里我使用了V*4个成员,目的是为了让散列速度更快,结果做到后面发现多此一举的做法让拓扑排序效率变得低下了。在只有V的容量下,使用的探测方式应该是线性探测法(虽然会使得最后几个插入的顶点效率低下),在这里我使用的是平方探测法。
2、散列方式:
在这里我使用的是对名字字符串的每个字符大小相加取模的方式:
/*改成对字符相加求模*/
int Hash(VertexType Key, int TableSize)
{
int temp=0;
while( *Key != '\0')
temp += *Key++;
return temp%TableSize;
}如果改成只有V个成员,线性探测,那么面临的问题:
1、插入顶点前先确认顶点数量,最后插入的几个顶点插入效率低下。根据顶点字符串名字寻址顶点序号复杂度为O(N)。
2、如果需要添加顶点,需要重新开辟新的哈希表,大小为V+1,并读入原有哈希表内容,开销巨大。
3、邻接表头文件:
将哈希表取别名为图,定义图的操作函数(大部分直接调用哈希表的成员函数即可),定义入度结构体(这里因为哈希表的节点数与定点数不等,所以需要记录顶点对应哈希表的位置)。
#include "HashTableOpenAdd.h"
#ifndef _ADJACENCY_LIST
#define _ADJACENCY_LIST
struct IndegreeNode;
typedef IndegreeNode* Indegree;
typedef HashTable Graph;
Graph intializeGraph(int VertexNum);
void insertEdge(VertexType vertex1, VertexType vertex2, WeightType weight, Graph G);
void insertVertex(VertexType vertex, Graph G);
Position findVertex(VertexType vertex, Graph G);
void removeEdge(VertexType vertex1, VertexType vertex2, Graph G);
void DestroyGraph(Graph G);
void PrintGraph(Graph G);
Indegree getIndegree(Graph G);
void PrintIndegree(Indegree D, Graph G, int total);
int* TopSort(Graph G, Indegree D);
void PrintTopSort(int * TopNum, Graph G);
struct IndegreeNode
{
Index vertexIndex;
int indegreenum;
};
#endif
编码实现:
1、初始化:
这里新建的哈希表是顶点个数的4倍。这是最初的实现。我打算在之后重构整个代码。
/*初始化图*/
Graph intializeGraph(int VertexNum)
{
return initializeTable(VertexNum*4);
}
插入顶点:
/*插入顶点,直接调用哈希表的插入键值*/
void insertVertex(VertexType vertex, Graph G)
{
insertKey(vertex, G);
G->vertex++;
}
插入边:
/*插入边,需要先进行判断边的两个顶点是否存在,不存在则先插入顶点*/
void insertEdge(VertexType vertex1, VertexType vertex2, WeightType weight, Graph G)
{
Position P1, P2;
P1 = FindKey(vertex1, G);
P2 = FindKey(vertex2, G);
if(G->TheCells[P2].Info != Legitimate)
insertVertex(vertex2, G);
if(G->TheCells[P1].Info != Legitimate)
insertVertex(vertex1, G);
/*加入新的边*/
Edge newEdge = (Edge)malloc(sizeof(EdgeNode));
newEdge->vertexIndex = P2;
newEdge->weight = weight;
newEdge->next = G->TheCells[P1].next;
G->TheCells[P1].next = newEdge;
/*边数加一*/
G->edge++;
}
寻找顶点索引:
/*寻找顶点索引*/
Position findVertex(VertexType vertex, Graph G)
{
return FindKey(vertex, G);
}
移除边:
/*移除边,先确认顶点存在*/
void removeEdge(VertexType vertex1, VertexType vertex2, Graph G)
{
Position P1, P2;
P1 = FindKey(vertex1, G);
P2 = FindKey(vertex2, G);
if(G->TheCells[P2].Info != Legitimate && G->TheCells[P1].Info == Legitimate)
{
fprintf(stderr, "Edge not exist\n");
return;
}
VertexNode * V = &G->TheCells[P1];
Edge parent = V->next;
/*判断该边是否是第一条边*/
if(parent->vertexIndex == P2)
{
V->next = parent->next;
free(parent);
}
else
{
Edge temp;
while(parent->next->vertexIndex != P2)
parent = parent->next;
temp = parent->next;
parent->next = temp->next;
free(temp);
}
}
删除图:
/*删除图,需要先删除边,再调用删除哈希表*/
void DestroyGraph(Graph G)
{
for(int i =0; i<G->TableSize; i++)
if(G->TheCells[i].Info == Legitimate &&G->TheCells[i].next != NULL)
DestroyEdge(G->TheCells[i].next);
DestroyTable(G);
}
打印图:
/*打印图*/
void PrintGraph(Graph G)
{
for(int i =0; i<G->TableSize; i++)
if(G->TheCells[i].Info == Legitimate)
PrintEdge(&G->TheCells[i], G);
}
测试结果:
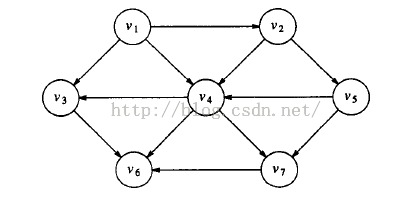
在这里使用课本218页的有向无圈图进行测试,输入每一条边即可。
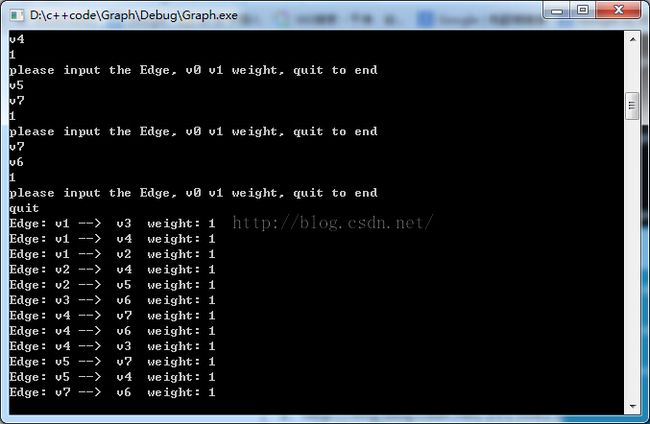
输出的结果图:
拓扑排序:
拓扑排序需要两个输入参数,邻接表和入度数组。
在这里我们先说第一步,如何生成入度数组。
1.如果哈希表空间对应顶点数V,那么非常简单:
仅仅需要V+E的复杂度。做法是开辟一个顶点数V的数组。直接对邻接表中每条边记录的顶点v进行计数
Indegree[v]++;如此,遍历一遍图即可得到。
2.哈希表空间不对应顶点数V(现在我的做法)
这样的话还是需要开辟大小为顶点数V的结构体数组
结构体定义:
struct IndegreeNode
{
Index vertexIndex;
int indegreenum;
};第一个记录该点的序号,另一个记录入度数。
生成方式如下:
1.遍历哈希表,将每个顶点的序号记录在入度表中,入度初始化为0;
2.遍历所有边,对每个末尾顶点对应的Indegree表中的入度数加1(由于不能直接寻址到Indegree表中的顶点,在这里需要再次遍历入度表,复杂度为O(V),因此总的复杂度变成了O(V*E))。效率过于低下。
这里我的实现如上所述过于复杂,我打算之后再次重构实现。
编码实现:
Indegree getIndegree(Graph G)
{
int num = G->vertex;
Indegree indegree;
int count=0;
indegree = (Indegree)calloc(num, sizeof(IndegreeNode));
for(int i=0; i<G->TableSize; i++)
if(G->TheCells[i].Info == Legitimate)
indegree[count++].vertexIndex = i;
for(int i=0; i<num; i++)
countIn(i, indegree, G);
return indegree;
}
/*计算每个顶点的入度数*/
void countIn(int num, Indegree D, Graph G)
{
int total = G->vertex;
Index P = D[num].vertexIndex;
for(int i=0; i<total; i++)
{
Index temp = D[i].vertexIndex;
if(temp != P)
{
/*如果该顶点有一个指向所求顶点的边,则入度加一*/
if(findEdge(&G->TheCells[temp], P))
D[num].indegreenum++;
}
}
}
拓扑排序:无论入度表的生成怎么样复杂,进行拓扑排序的方式还行相同的。
1.读入入读表,找到入度为0的顶点,加入队列。
2.队列出队,输出第一个顶点,将该顶点为起点,对应终点的顶点的入度减一(在这里实现时,又要遍历入度表来寻找对应的顶点,导致复杂度变成了O(V*E))。
3.在过程2中入度变成1的顶点入队。
4.循环过程(2,3)直到队列空。
编码实现:
/*拓扑排序*/
int* TopSort(Graph G, Indegree D)
{
Queue Q;
Q = createQueue();
int num = G->vertex;
int * TopNum = (int *)calloc(G->vertex, sizeof(int));
if(TopNum == NULL)
{
fprintf(stderr, "not enough memory\n");
exit(1);
}
for(int i=0; i<num; i++)
{
if(D[i].indegreenum == 0)
enqueue(D[i].vertexIndex, Q);
}
int count =0;
Index V;
while(!isEmpty(Q))
{
V = dequeue(Q);
TopNum[count++] = V;
Edge edge = G->TheCells[V].next;
while(edge != NULL)
{
if(decreaseDegree(edge->vertexIndex, D, num) == 0)
enqueue(edge->vertexIndex, Q);
edge = edge->next;
}
}
/*删除队列*/
disposeQueue(Q);
if(count != num)
{
fprintf(stderr,"Graph has a cycle\n");
free(TopNum);
return NULL;
}
return TopNum;
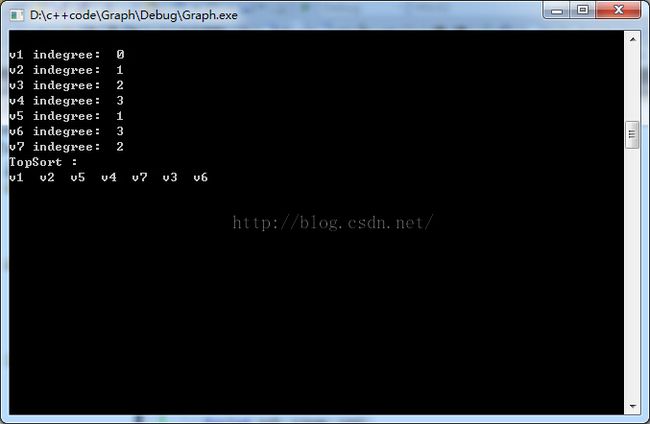
}测试结果:
同样还是输如上的有向图,一共有七个顶点。
最终输出结果正确。
总结:
这次实现邻接表应该算是一次突破。课本上只说了邻接表的大概实现,使用与哈希表结合的方式。自己经过尝试,最终实现出来了邻接表并且完成了拓扑排序。只不过由于最开始的思考还不够细致,导致算法的复杂度上升了。我将重构这部分代码,并且作为一个新版本贴出来(多亏最初的函数做到了高聚合低耦合)。