KNN(k-nearest neighbor algorithm)--从原理到实现
零.广告
本文所有代码实现均可以在 DML 找到,不介意的话请大家在github里给我点个Star![]()
一.引入
K近邻算法作为数据挖掘十大经典算法之一,其算法思想可谓是intuitive,就是从训练集里找离预测点最近的K个样本来预测分类
因为算法思想简单,你可以用很多方法实现它,这时效率就是我们需要慎重考虑的事情,最简单的自然是求出测试样本和训练集所有点的距离然后排序选择前K个,这个是O(nlogn)的,而其实从N个数据找前K个数据是一个很常见的算法题,可以用最大堆(最小堆)实现,其效率是O(nlogk)的,而最广泛的算法是使用kd树来减少扫描的点,这也就是这篇文章的主要内容,本文偏实现,详细理论教程见july的文章 ,不得不服,july这篇文章巨细无遗!
二.前提:堆的实现
堆是一种二叉树,用一个数组存储,对于k号元素,k*2号是其左儿子,k*2+1号是其右儿子
而大根堆就是跟比左儿子和右儿子都大,小根堆反之。
要满足这个条件我们需要通过up( index )操作和down( index )维护它的结构
当然讲这个的文章实在有些多了,随便搜一篇大家看看:点击打开链接
大小根堆的作用是
a) 优先队列:因为第一个元素是最大或者最小的元素,所以可以实现优先队列
b) 前K个最大(最小)值:这里限制堆的大小为k,来获得O( n log k)的效率,但注意此时小根堆是获得前K个最大值,大根堆是获得前K个最小值,插入的时候先把元素和堆顶比较再决定是否插入。
因为事先KD-tree+BBF 要同时用到这两个东西,所以把它们实现在了同一个类里,感觉代码略漂亮,贴出来观赏一下:
此代码是dml / tool / heap.py
from __future__ import division
import numpy as np
import scipy as sp
def heap_judge(a,b):
return a>b
class Heap:
def __init__(self,K=None,compare=heap_judge):
'''
'K' is the parameter to restrict the length of Heap
!!! when K is confirmed,the Min heap contain Max K elements
while Max heap contain Min K elements
'compare' is the compare function which return a BOOL when pass two variable
default is Max heap
'''
self.K=K
self.compare=compare
self.heap=['#']
self.counter=0
def insert(self,a):
#print self.heap
if self.K!=None:
print a.x,'==='
if self.K==None:
self.heap.append(a)
self.counter+=1
self.up(self.counter)
else:
if self.counter<self.K:
self.heap.append(a)
self.counter+=1
self.up(self.counter)
else:
if (not self.compare(a,self.heap[1])):
self.heap[1]=a
self.down(1)
return
def up(self,index):
if (index==1):
return
'''
print index
for t in range(index+1):
if t==0:
continue
print self.heap[t].x
print
'''
if self.compare(self.heap[index],self.heap[int(index/2)]):
#fit the condition
self.heap[index],self.heap[int(index/2)]=self.heap[int(index/2)],self.heap[index]
self.up(int(index/2))
return
def down(self,index):
if 2*index>self.counter:
return
tar_index=0
if 2*index<self.counter:
if self.compare(self.heap[index*2],self.heap[index*2+1]):
tar_index=index*2
else:
tar_index=index*2+1
else:
tar_index=index*2
if not self.compare(self.heap[index],self.heap[tar_index]):
self.heap[index],self.heap[tar_index]=self.heap[tar_index],self.heap[index]
self.down(tar_index)
return
def delete(self,index):
self.heap[index],self.heap[self.counter]=self.heap[self.counter],self.heap[index]
self.heap.pop()
self.counter-=1
self.down(index)
pass
def delete_ele(self,a):
try:
t=self.heap.index(a)
except ValueError:
t=None
if t!=None:
self.delete(t)
return t
传入的时候不设置K就是正常的优先队列,设置了K就是限制堆的大小了
compare参数是比较大小的,默认是“数”的大根堆,你可以往堆里传任何类,只要有相适应的compare参数,比如我们KD-tree传的就是KD-Node
三.KD-BFF的原理:
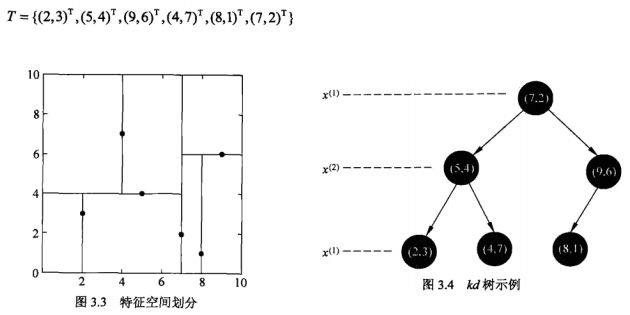
首先从KD-Tree的创建说起:(直接贴《统计学习方法》的内容了)
事实上从选择哪一个feature开始切割,还可以选择方差最大的那个参数,但是考虑到简便,以及我们可以选择更多的相似性度量方法,还是用《统计学习方法》里面的选择方式了。
然后是KD-tree搜索的方法:(来自《统计学习方法》,但注意这里是最近邻,也就是k=1的时候)
那么我们要K近邻要怎么做呢?就是用堆的第二个应用,用大根堆保持K个最小的距离,然后用根的距离(也就是其中最大的一个)来作为判断的依据是否有更近的点不在结果中,这一点很重要!
同时摘录july博客的一段读者留言讲得非常好的:
在某一层,分割面是第ki维,分割值是kv,那么 abs(q[ki]-kv) 就是没有选择的那个分支的优先级,也就是计算的是那一维上的距离; 同时,从优先队列里面取节点只在某次搜索到叶节点后才发生,计算过距离的节点不会出现在队列的,比如1~10这10个节点,你第一次搜索到叶节点的路径是1-5-7,那么1,5,7是不会出现在优先队列的。换句话说,优先队列里面存的都是查询路径上节点对应的相反子节点,比如:搜索左子树,就把对应这一层的右节点存进队列。
大致这就是我们实现的基本思路了
四.KD-BFF的实现:
知道原理了,并且有了堆这个工具之后我们就可以着手实现这个算法了:(终于要贴代码了)
代码~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~此代码是 dml / KNN / kd.py
from __future__ import division import numpy as np import scipy as sp from operator import itemgetter from scipy.spatial.distance import euclidean from dml.tool import Heap class KDNode: def __init__(self,x,y,l): self.x=x self.y=y self.l=l self.F=None self.Lc=None self.Rc=None self.distsToNode=None class KDTree: def __init__(self,X,y=None,dist=euclidean): self.X=X self.k=X.shape[0] #N self.y=y self.dist=dist self.P=self.maketree(X,y,0) self.P.F=None def maketree(self,data,y,deep): if data.size==0: return None lenght = data.shape[0] case = data.shape[1] p=int((case)/2) l = (deep%self.k) #print data data=np.vstack((data,y)) data=np.array(sorted(data.transpose(),key=itemgetter(l))).transpose() #print data y=data[lenght,:] data=data[:lenght,:] v=data[l,p] rP=KDNode(data[:,p],y[p],l) #print data[:,p],y[p],l if case>1: ldata=data[:,data[l,:]<v] ly=y[data[l,:]<v] data[l,p]=v-1 rdata=data[:,data[l,:]>=v] ry=y[data[l,:]>=v] data[l,p]=v rP.Lc=self.maketree(ldata,ly,deep+1) if rP.Lc!=None: rP.Lc.F=rP rP.Rc=self.maketree(rdata,ry,deep+1) if rP.Rc!=None: rP.Rc.F=rP return rP def search_knn(self,P,x,k,maxiter=200): def pf_compare(a,b): return self.dist(x,a.x)<self.dist(x,b.x) def ans_compare(a,b): return self.dist(x,a.x)>self.dist(x,b.x) pf_seq=Heap(compare=pf_compare) pf_seq.insert(P) #prior sequence ans=Heap(k,compare=ans_compare) #ans sequence while pf_seq.counter>0: t=pf_seq.heap[1] pf_seq.delete(1) flag=True if ans.counter==k: now=t.F #print ans.heap[1].x,'========' if now != None: q=x.copy() q[now.l]=now.x[now.l] length=self.dist(q,x) if length>self.dist(ans.heap[1].x,x): flag=False else: flag=True else: flag=True if flag: tp,pf_seq,ans=self.to_leaf(t,x,pf_seq,ans) #print "=============" #ans.insert(tp) return ans def to_leaf(self,P,x,pf_seq,ans): tp=P if tp!=None: ans.insert(tp) if tp.x[tp.l]>x[tp.l]: if tp.Rc!=None: pf_seq.insert(tp.Rc) if tp.Lc==None: return tp,pf_seq,ans else: return self.to_leaf(tp.Lc,x,pf_seq,ans) if tp.Lc!=None: pf_seq.insert(tp.Lc) if tp.Rc==None: return tp,pf_seq,ans else: return self.to_leaf(tp.Rc,x,pf_seq,ans)
然后KNN就是对上面这个类的一个包装:
代码~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~此代码是 dml / KNN / knn.py
#coding:utf-8
import numpy as np
import scipy as sp
from scipy.spatial.distance import cdist
from scipy.spatial.distance import euclidean
from dml.KNN.kd import KDTree
#import pylab as py
class KNNC:
"""docstring for KNNC"""
def __init__(self,X,K,labels=None,dist=euclidean):
'''
X is a N*M matrix where M is the case
labels is prepare for the predict.
dist is the similarity measurement way,
The distance function can be ‘braycurtis’, ‘canberra’,
‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’,
‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’,
‘mahalanobis’,
'''
self.X = np.array(X)
if labels==None:
np.zeros((1,self.X.shape[1]))
self.labels = np.array(labels)
self.K = K
self.dist = dist
self.KDTrees=KDTree(X,labels,self.dist)
def predict(self,x,k):
ans=self.KDTrees.search_knn(self.KDTrees.P,x,k)
dc={}
maxx=0
y=0
for i in range(ans.counter+1):
if i==0:
continue
dc.setdefault(ans.heap[i].y,0)
dc[ans.heap[i].y]+=1
if dc[ans.heap[i].y]>maxx:
maxx=dc[ans.heap[i].y]
y=ans.heap[i].y
return y
def pred(self,test_x,k=None):
'''
test_x is a N*TM matrix,and indicate TM test case
you can redecide the k
'''
if k==None:
k=self.K
test_case=np.array(test_x)
y=[]
for i in range(test_case.shape[1]):
y.append(self.predict(test_case[:,i].transpose(),k))
return y
因为KNN毕竟是一个分类算法,所以我在predict是加上了分类的代码,如果只想检验Kd-tree的话,你可以直接用for_point()找最近k个点
五.测试+后记
测试:
我们选取《统计学习方法》上面的例子:
使用代码:
X=np.array([[2,5,9,4,8,7],[3,4,6,7,1,2]]) y=np.array([2,5,9,4,8,7]) knn=KNNC(X,1,y) print knn.for_point([[6.5],[7]],1)这里y是label,是用来预测的,这个例子里没有实际作用,这是用来分类的
输出中后面带了“===”的是扫描过的点,最后的是搜索的结果:
我们可以看到的确避免扫描了(2,3),Bingo!!
我们再knn.for_point([[2],[2]]):可以看到避免扫了很多点!!!
后记:
从实现写此文前后耗时两天,昨天写代码写到熄灯且刚好测试通过,怎一个爽字了得!!最后,再在github上求个Star
reference:
【1】从K近邻算法、距离度量谈到KD树、SIFT+BBF算法 http://blog.csdn.net/v_july_v/article/details/8203674
【2】《统计学习方法》 李航
【3】最大堆的插入/删除/调整/排序操作(图解+程序) http://www.java3z.com/cwbwebhome/article/article1/1362.html?id=4745