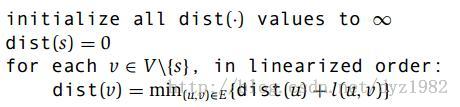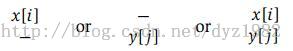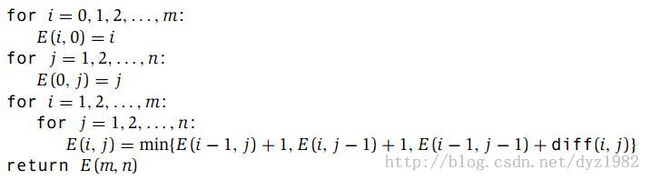计科1111-1114班第七周讲义、课外作业(动态规划,截止日期:2014年4月25日23点-周五晚,学委飞信通知同学)
《算法设计与分析》课程中,作业所指教材,均为《算法概论》(Sanjoy Dasgupta等,清华大学出版社,2008年7月第1版)。
第7周,主要对教材 第6章 动态规划 进行了探讨。Dynamic Programming(简称DP),是一个通用的问题求解方法,主要用于运筹学方面的最优化问题,由于其对思维能力的高要求,很受各大公司笔试、面试欢迎。同学们在开始学习时,可以循序渐进,先理解教材中问题的精要并总结,然后去编程实现2-3个问题,最后去网上找3-10道笔试、面试题求解来开拓思路。
一:作业内容
二:作业要求
1. 请各班学委飞信通知同学完成作业。
2. 作业计入平时成绩,计分依据为大家的完成程度——态度(做 / 未做)。老师会根据大家作业的质量选择若干学生进行评论,以及提供个性化教学的依据。请大家依据自身能力,尽可能提供高水平的作业,为提高自身能力全力以赴。
3. 本次作业,老师主要检查本班学号位于11-20号的同学 和 申请免签到的同学,以及抽查部分其他同学,请大家相互转告。
三:提前预习
预习 第7章 线性规划与归约(P205开始)。理解线性规划问题的提出、网络流问题、二部图匹配,重点为单纯形算法(P232-241)。
四:推荐阅读
成功不是偶然,对编程或其他方面的兴趣也是一个过程。只有当我们了解一些基础后,才可能产生并激发兴趣。这里通过一篇博文,看一下大家的学长 郝中奎 的编程之路,以及软件专业大三学生骆宏的兴趣之路。
五:讲授内容(整理)
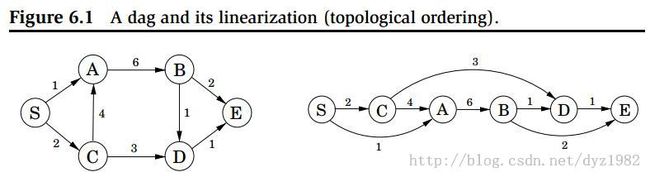
(1)有向无环图的最短路径问题。Directed acyclic graph(简称:DAG),这是我们第3次、第4次接触到有向无环图的应用了。首先大家回顾一下,DAG有哪些特性?前面的章节中我们哪些问题有DAG有关?对DAG,我们又开展了哪些工作?温故而知新。
DAG的一个重要性质是节点可以进行线性排列(拓扑排序),可以使用深度优先搜索(DFS),并标记每一个节点的第一次访问(pre)和最后一次访问时间(post),最后post的逆序就是DAG的拓扑排序,其实也是节点在进行DFS搜索时,出栈的逆序就是拓扑排序。
怎样计算DAG的最短路径呢?第4章(P135-136)我们按照图中节点的拓扑排序的顺序依次计算节点的距离,其计算思路进一步可以表述如下所示的递推公式。
所以计算源点S到节点D的距离,可以通过先计算S到B、S到C的距离后,利用上述公式求解。以此类推,最终我们可以通过依次计算S到S、S到C、S到A……等把每个节点的距离计算出来。算法如下:
要点:任何一个动态规划问题,都可以等价为一个有向无环图DAG问题。
(2)动态规划的两个基本性质。(a)最优子结构性质:如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理);(b)重叠子问题性质:子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
(3)最长递增子序列。输入类似下图中的一个数字序列,从中按顺序挑选一个子集,使得该子序列中数字满足严格单调递增关系。如下面,数列中的2、3、6、9 与 2、3、6、7等数列就是该数列的最长递增子序列。怎样计算呢?利用动态规划方法的性质,我们需要思考得到一个重叠子问题的结构。思考:如果2、3、6、9是一个最长递增子序列,那么去掉最后数字9与7之后,2、3、6也是数列5、2、8、6、3、6的最长递增子序列(最优子结构性质)。所以计算包括某一个数字(如9)并到该数字结束的的最长递增子序列,可以考虑该数字之前的子序列(5、2、8、6、3、6)中与9满足严格递增关系的数字(如 5、2、8、6、3、6),如果计算得到了5、2、8、6、3、6等数字的最长递增子序列,选择其中最长的一条,则可以得到包括9在内的最长递增子序列。运算关系见下下图。
未完待续……
(4)编辑距离。查找两个单词的相似度,在拼写检查等很多场合中都有应用。前面我们补充过 利用余弦定理与TF-IDF来计算文档相似性(TF-IDF与余弦相似性的应用(一):自动提取关键词,TF-IDF与余弦相似性的应用(二):找出相似文章),今天我们学习另一种距离定义方式。
编辑距离:将一个字符串变换为另一个字符串所需最小编辑操作——包括插入、删除、字符替换的次数(教材P178)。如下图中两个单词SNOWY和SUNNY,第一种方式次数为3,第二种方式次数为5,但由于编辑距离指的是最小编辑操作,所以这两个单词的编辑距离为3。把上面这个单词变换为下面单词,只需要在S后插入U,把O替换为N,删除W,一共三个操作(当然还有其他方式)。
怎样把编辑距离的问题用动态规划方法求解,首先需要定义最优子结构。把单词 x[1···m] and y[1···n] 分成两部分:前缀部分和剩余部分,如前缀(Prefix)部分x[1···i] 和 y[1···j],定义编辑距离的子问题E(i,j),则原问题即为计算E(m,n)。如 x[1···i] 和 y[1···j],其对齐方式有三种(如下图,教材P179)。
如两个单词 EXPONENTIAL与POLYNOMIAL,其E(7,5)如下图所示。现在我们就可以写出递归形式了。 E(i,j)=min{1+E(i −1,j), 1+E(i,j −1), diff(i,j)+E(i −1,j −1)} ,寻找三种对齐方式下的最小编辑距离,并且成功的把E(i,j)问题转化为求解 E(i −1,j),E(i,j −1),E(i −1,j −1)等小一点的问题。
明白了这一点,我们就可以按照算法伪代码,编出具体程序代码了。请思考图6-4(教材P180),在计算得到编辑距离E(m,n)后,我们怎样得到两个字符串的对齐方式呢?怎样增加最少的代码实现呢?
(5)背包问题。网上有经典的 背包问题九讲,以及在此基础上的进一步学习(背包问题九讲笔记_01背包),研究与总结的人很多,如背包问题 笔试题,大家需要掌握单副本下的背包问题(教材P185)。
单副本的背包问题(Knapsack without repetition):N件物品,分别重w1,...,wn,价值为v1,...,vn,现有一个背包最大容量为W,怎样的组合才能够使背包中装下的物品价值最高?
摘自: knapsack-problem(http://www.answers.com/topic/knapsack-problem)
假设我们对物品进行编号,则问题转化为 W=15,且物品编号、重量与价值如下表所示。为此,定义子问题,使包含关于哪件物品已经被使用过的信息,引入两个参数w、j,定义如下
K(w,j) = 基于背包容量w和物品1,…,j所能得到的最高价值,其中0≤j ≤n
| 物品 | 重量 | 价值 |
| 1 | 4 | 10 |
| 2 | 12 | 4 |
| 3 | 1 | 2 |
| 4 | 2 | 2 |
| 5 | 1 | 1 |