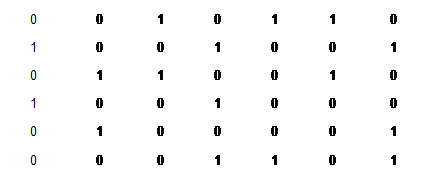简单易懂的Dancing links讲解(2)
Dancing Links一般都用来解决精确覆盖问题,什么是精确覆盖问题呢?就是下面这种:
DancingLinks精确覆盖
题目描述
对于如下01矩阵,选择若干行,使得矩阵的每一列都有且仅有一个11,4,5行,是精确覆盖的一个解,如何用Dancing Link得到这个解的,可以参考代码
http://blog.csdn.net/acmer1183/article/details/6320437
接下来重点讲解,对于这个题目,dance links的具体的舞蹈步骤和过程,也就是对如上参考程序的详解
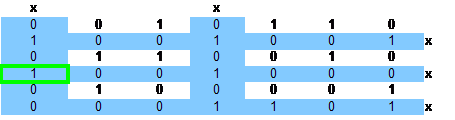
首先,选择2行1列后(即绿框所在的行),带来效应是:1,4,7列都被删除了,2,4,5,6行也被删除了
| x | x | x | |||||
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | x |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | x |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | x |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | x |
图中被染色的行列,表示这些行列已经被删除了,绿框所在的行表示,当前选择的是第几行
尚有2,3,5,6列有待删除,dancinglink还需继续dancing
我们选择包含1最少的列来删除,现在包含1最少的列是第2列
| x | x | x | x | x | x | ||
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | x |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | x |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | x |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | x |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | x |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | x |
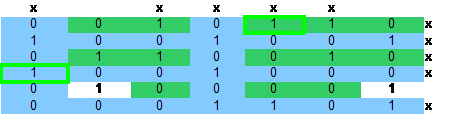
在进行回溯时,由于第3行2列的单元格没有兄弟节点;也就是说这个单元格所在的列,当时有 且仅有一个1
这里着重解释一下“当时”:本来,3行2列的单元格(绿色单元格)是有一个兄弟节点(5行2列的单元格)的,
但这个兄弟节点在dancing的前一步就已经被剔除掉了并且被染成蓝色,是因为我们之前选择了1列2行的元素
兄弟关系:在同一列不同行的值为1的单元格,并且这些单元格的颜色相同,这样这些单元格才有兄弟关系
发现选择2,3行无解,开始回溯,直接回溯成下图这样:
继续dancing,选择含1最少的列
继续dancing,选择含1最少的列
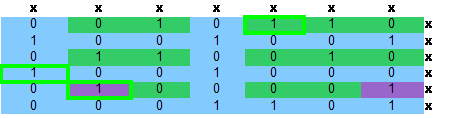
现在,所有的列都被删除了,所以选择1,4,5行,是精确覆盖的一个解