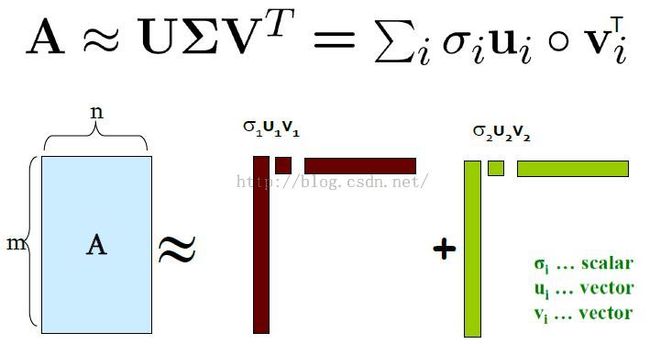海量数据挖掘MMDS week4: 推荐系统之数据降维Dimensionality Reduction

http://blog.csdn.net/pipisorry/article/details/49231919

海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记 推荐系统Recommendation System之降维Dimensionality Reduction

{博客内容：推荐系统有一种推荐称作隐语义模型(LFM, latent factor model)推荐，这种推荐将在下一篇博客中讲到。这篇博客主要讲隐语义模型的基础：降维技术，包括SVD分解等等}

降维Dimensionality Reduction

降维介绍

数据的低维表示：空间中的点不是完全随机分布的，它们分布在某个子空间中。the idea is that these points are not just randomly scattered through the space,but they lie in a subspace of it.

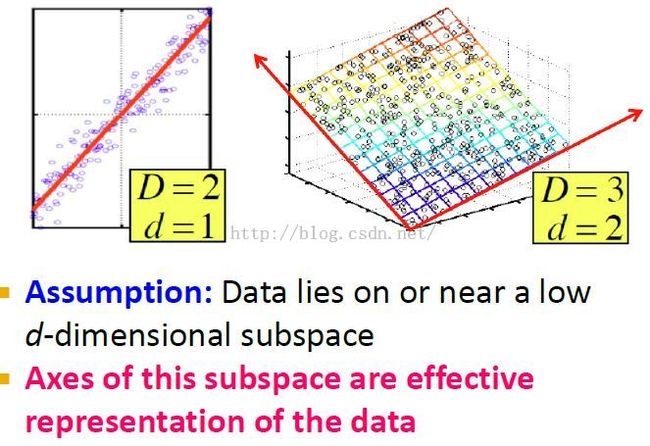
我们的目标就是找到这个可以有效表示所有数据的子空间。

降维示例

customer-day矩阵中行表示data（也就是点），列代表数据属性（也就是点的坐标）。降维就是要减少属性（列）。

这个矩阵实际只有2维，wc-th-fr和sa-su。

数据集的维度

矩阵的秩

矩阵A的秩就是A中列的无关最大组数目。下面的是坐标重新定义后A矩阵的表示。

秩即维数

通过秩来进行坐标重定义，用新坐标重新表示A矩阵，达到降维目的。

降维的实质

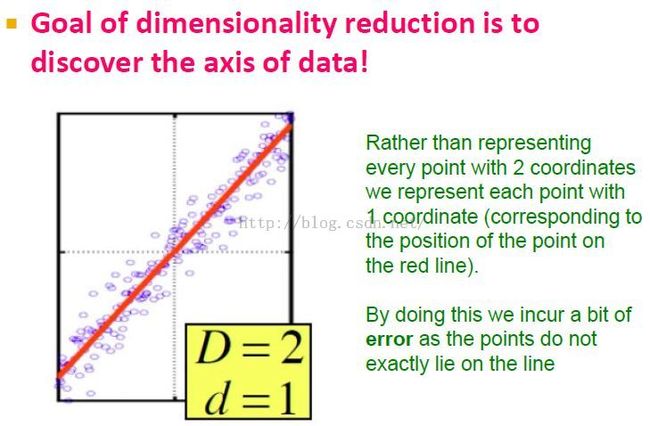
实质是找到一个新的数据轴。

这个例子中，我们只考虑数据在红线上的投影，而忽略与红线的距离，存在一定的error。目标就是找到一个新坐标轴让error尽量小。

降维的目的

皮皮blog

奇异值分解Singular Value Decomposition, SVD

{数据降维技术1}

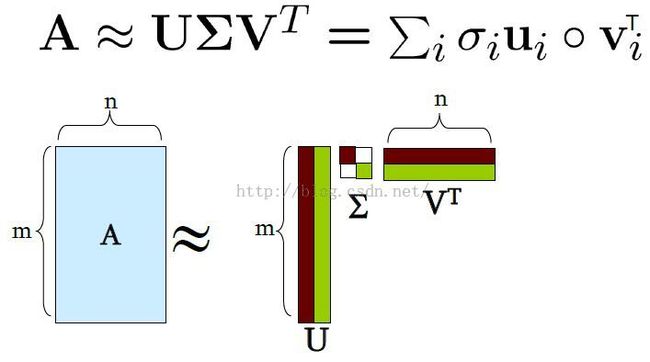
SVD定义

这里假设奇异值对角矩阵中的奇异值是降序排列的。

   

[矩阵论]

SVD分解的性质

Note: U、V列向量是正交的orthogonal，也就是说向量间内积为0。

SVD分解实例

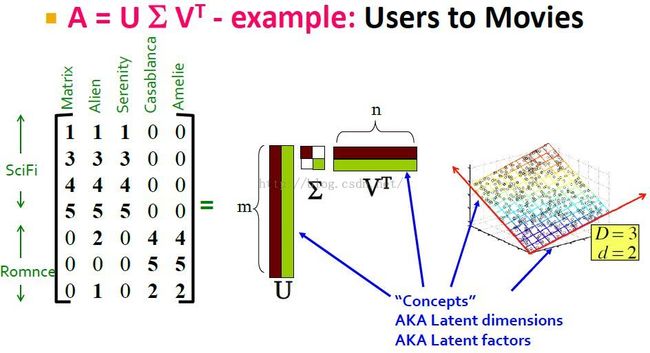
users-movies矩阵，其中行代表用户，每列代表一部电影。

concepts就是SVD分解要告诉我们的，用户是sci-fi lover和romance lover类型，电影是sci-fi和romance等类型。也就是不同的genres（流派）, or topics。

SVD分解中各分解分量的实际意义解释

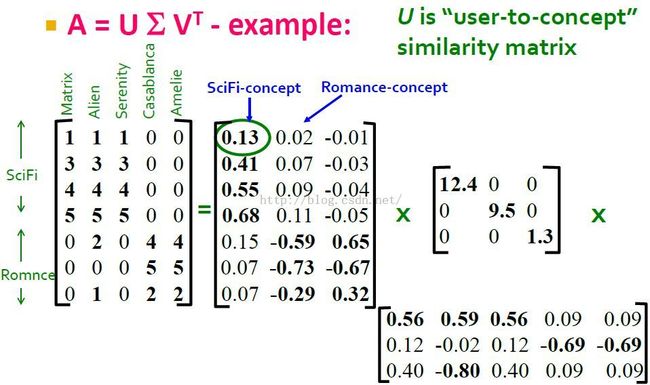
下面是通过matlab或者python对矩阵A进行SVD分解得到的结果。下面分别讲解U V矩阵代表的实际含义（注意这种解释性也是人为解释的，其实SVD分解的解释性并没有那么强）。

我们可以将U的列看成concepts，如U的第一列对应Sci-Fi concept，第二列对应romance concept（第三列可能代表其它的什么，其实不一定能用一个类别来描述和解释，因为SVD其解释性并不是那么强）。我们从这里可以看到，前4个用户衷情于sic-fi，后3个用户衷情于romance。

于是我们可以将U矩阵看成是user to concept matrix(user to concept similarity matrix)。其中元素代表某个用户对某个concepts的感兴趣程度。这里是说第1个用户很喜欢sci-fi concept（0.13），而第5个用户很喜欢romance concept（-0.59）。至于-0.59代表最喜欢的concept，可能是要看它的绝对值？

Sigma矩阵中的值可看做是concepts的强度，如sci-fi concept强度（12.4）就比romance concept的强度（9.5）强。

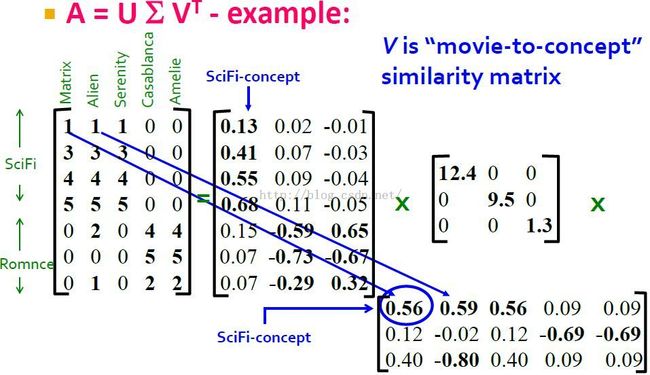
同样的，我们可以将V矩阵看成是movies to concept matrix(movies to concept similarity matrix)。注意这里还有第三种concepts，但是其强度1.3太小，可以忽略。

从V矩阵第1列我们可以看到，第1部电影与第1个concept和第3个concept相关度高，然而第3个concept的强度过低，它对解释数据并不重要。

[TopicModel主题模型 - LSA（隐性语义分析）模型和其实现的早期方法SVD]

皮皮blog

Review复习

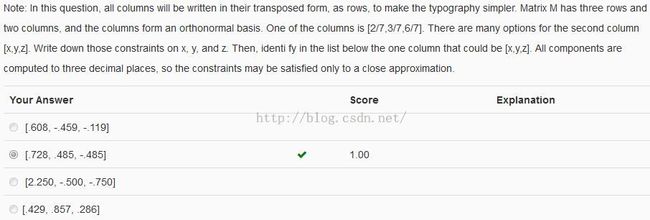
标准正交基

计算出各个选项的长度（2范数）和与[2/7...]的内积为：

0.771042151896
-0.125

1.00021697646
0.000142857142857

2.42383992871
-0.214285714286

1.00014298978
0.735

故选择选项2

Code:

a = np.array([2 / 7, 3 / 7, 6 / 7])
B = [[.608, -.459, -.119], [.728, .485, -.485], [2.250, -.500, -.750], [.429, .857, .286]]
for b in B:
    print(np.linalg.norm(b))
    print(a.dot(b))
    print()

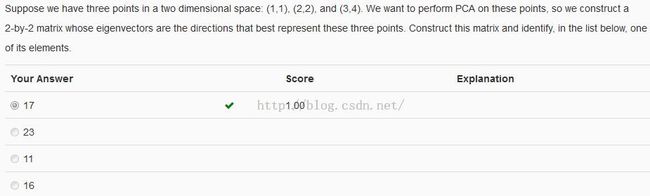
PCA

皮皮blog

from: http://blog.csdn.net/pipisorry/article/details/49231919

ref: