Hadoop准备篇之(一):Page Rank算法初探
为什么会将Page Rank放在hadoop学习笔记里,是因为hadoop课程第一周就重点提到了Google当年三大论文(GFS, Map-Reduce和Big Table)以及hadoop思想的来源,并提到了page rank与Map-reduce解决方案下的PR算法,关于如何应用分布式计算来处理上万亿网页的Page rank的Map-reduce思想现在还没有搞清楚,在这之前,颇费了些周章去理解page rank的基本算法。有几篇文章讲述得非常清楚,(更是觉得数学是趋势所需,没有好的数学包括线性/高数/离散等很多路径将走不通)
说实话,培训课件中关于Page Rank算法的讲解实在是太抽象了,而且矩阵也没有说明白为什么必须得长成那样,比如行是啥意思,列是啥意思,为什么必须得乘以个4行1列的列,还有这个收敛函数(PG)公式又是怎样得来的,为什么要乘来乘去的,我接连听了三遍都没听明白,终于在这儿找到想要的答案了...
博主用与课件中相同的路径关系,讲解了上面这些我在听课件时遗留下来的问题,
>> http://blog.codinglabs.org/articles/intro-to-pagerank.html (真的写得非常清楚)
另外,这儿有两个关于Page Rank算法的小web app,可以自行拖动页面关系,计算G值 https://googledrive.com/host/0B2GQktu-wcTiaWw5OFVqT1k3bDA/ ,其算法解释为http://www.nowherenearithaca.com/2013/04/explorating-googles-pagerank.html 这个算法中加上了dead end的1/6的矩阵,我不知道是否必要,毕竟后面已经有加上一个(1-alpha) * 1/page count的矩阵了。
群里面一直有人没明白googler当时整出这个0.85的alpha值究竟是干嘛的,而下述算法公式又是怎么得出的, 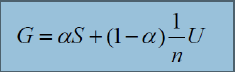
因为培训的第一周作业就是使用代码计算page rank,我也在代码中试验了一下这个值存在必要性。
hyperlink matrix中的你看到的数值1/3,1/3,1/3 是用户在当前页面跳转到链接网站的概率,但如果有某个页面它为只有链出没有链进(或干脆完全孤立的话)被称为dead end,则处于这个matrix中容易造成一些页面的vector都为0,
比如我将第一题的matrix改一下,使得没有任何页面链向A,
/* A B C D E */
/*A*/ { 0, 0, 0, 0, 0 },
/*B*/ { 1/3f, 0, 0, 0, 0 },
/*C*/ { 1/3f, 0, 0, 1/2f, 1 },
/*D*/ { 1/3f, 1/2f, 0, 0, 0 },
/*E*/ { 0, 1/2f, 1, 1/2f, 0 }
直接从原hyperlink matrix算迭代的结果:
Staring iteration 4...
0 0*0 0*0 0*0.5 0*0 0*0.5 <0>
1 0.3333333*0 0*0 0*0.5 0*0 0*0.5 <0>
2 0.3333333*0 0*0 0*0.5 0.5*0 1*0.5 <0.5>
3 0.3333333*0 0.5*0 0*0.5 0*0 0*0.5 <0>
4 0*0 0.5*0 1*0.5 0.5*0 0*0.5 <0.5>
可以看到仅仅是这样就造成了B和D的PR也为0,这是不正确的。
所以googler们想出一个可能性,就是用户处于某个页面时,有极小概率(比如1-0.85)会去打开与页面无关的其它页面,这种称为称为teleporting
所以0.85 * hyperlink matrix,然后加上(剩余的即0.15/页面数,至于为什么要/页面数,可以理解为一个到任何页面的随机概率矩阵,即全为1/页面数的矩阵) 来使得这些没有链出的页面有极小的vector值,比如第一周题目中G MATRIX算出这些页面的“偏移后的”概率为0.03
这样就不会造成问题了。
加入teleporting后
Staring iteration 4...
0 0.03*0.02999999 0.03*0.0385 0.03*0.4361937 0.03*0.0548625 0.03*0.4404438 <0.02999999>
1 0.3133333*0.02999999 0.03*0.0385 0.03*0.4361937 0.03*0.0548625 0.03*0.4404438 <0.03849999>
2 0.3133333*0.02999999 0.03*0.0385 0.03*0.4361937 0.455*0.0548625 0.88*0.4404438 <0.4361937>
3 0.3133333*0.02999999 0.455*0.0385 0.03*0.4361937 0.03*0.0548625 0.03*0.4404438 <0.05486249>
4 0.03*0.02999999 0.455*0.0385 0.88*0.4361937 0.455*0.0548625 0.03*0.4404438 <0.4404437>
这是我在读文后的理解,有理解不一致的欢迎指正。
附上题目及解决方法,使用C#代码处理,用哪种语言没差了,
1. 基本过程就是:设置初始值hyperlink matrix (按概率的概念),通过公式 alpha=0.85 G= 0.85 * hyperlink matrix + (1-0.85)/页面数量 * 1 matrix 得到G矩阵
注意G矩阵每个PAGE(每列)的和不能超过1,否则结果会发散,应该等于1最后才能正确闭合。
之后所有运算基于固定G矩阵。qn+1 = Gqn
2. 迭代结束的收敛闭合条件:欧氏距离计算方法 《距离和相似度度量》
另外,初始向量数组q0的数值实验得出的结果是确实关系不大,5个1最后14次0.0001差值精确,5个0.2最后13次0.0001差值精确,唯一关系到出来的vector的倍数,但这些页面的比重是相同的。
题目:
1 参考根据幻灯片中第9页所给出的“4网页模型” ,现假设有A,B,C,D,E五个网页,其中
1)A网页有链接指向B,C,D
2)B网页有链接指向A,E
3)C网页有链接指向A,E
4)D网页有链接指向C
5)E网页有链接指向A,C
A 请写出这个网页链接结构的Google矩阵,目测你认为哪个页面的重要性(PR值)最高?
B 手动或编程计算这5个页面的PR值,可以使用任何你熟悉的编程语言,欢迎在论坛上晒自己的程序和结果 (可选)
C 指出当页面较多的时候,计算PR的主要困难在什么地方,Map-Reduce是怎么解决这个难题的? (可选)
using System;
namespace ConsoleApplication1
{
class Program
{
static float[,] arrSrcMatrix;
static float alpha = 0.85f;
static float[] curPageRankMatrix;
static int iterationTime;
static void Main(string[] args)
{
arrSrcMatrix = new float[5, 5]{
/* A B C D E */
/*A*/ { 0, 1/2f, 1/2f, 0, 1/2f },
/*B*/ { 1/3f, 0, 0, 0, 0 },
/*C*/ { 1/3f, 0, 0, 1, 1/2f },
/*D*/ { 1/3f, 0, 0, 0, 0 },
/*E*/ { 0, 1/2f, 1/2f, 0, 0 }
};
getGoogleMatrix();
curPageRankMatrix = new float[5] { 0.2f, 0.2f, 0.2f, 0.2f, 0.2f };
iterationTime = 0;
double endValue = 0.00001d;
while (1 == 1)
{
iterationTime++;
var nextMatrix = doIterate(curPageRankMatrix);
// 欧几里得距离(Euclidean Distance)
double cnt = 0.00d;
for (var m = 0; m < curPageRankMatrix.Length; m++)
{
cnt += Math.Pow(nextMatrix[m] - curPageRankMatrix[m], 2);
}
if (Math.Sqrt(cnt) <= endValue)
{
break;
}
else
{
curPageRankMatrix = nextMatrix;
}
}
}
/// <summary>
/// G = 0.85 * google matrix + 0.15/page count * one matrix
/// </summary>
static void getGoogleMatrix()
{
for (var m = 0; m <= arrSrcMatrix.GetUpperBound(0); m++)
{
Console.Write(string.Format("{0}\t", m));
for (var n = 0; n <= arrSrcMatrix.GetUpperBound(0); n++)
{
arrSrcMatrix[m, n] = arrSrcMatrix[m, n] * alpha + (1 - alpha) / (arrSrcMatrix.GetUpperBound(0) + 1);
Console.Write(string.Format("{0}\t", arrSrcMatrix[m, n]));
}
Console.WriteLine();
}
}
/// <summary>
/// current page rank matrix, shall be the number of pages
/// </summary>
/// <param name="curPageRankMatrix"></param>
static float[] doIterate(float[] curPageRankMatrix)
{
float[] tgt = new float[curPageRankMatrix.Length];
Console.WriteLine("Staring iteration " + iterationTime + "...");
for (var m = 0; m <= arrSrcMatrix.GetUpperBound(0); m++)
{
if (m >= tgt.Length) break;
float cur = 0.0f;
Console.Write(string.Format("{0}\t", m));
for (var n = 0; n <= arrSrcMatrix.GetUpperBound(0); n++)
{
cur += arrSrcMatrix[m, n] * curPageRankMatrix[n];
Console.Write(string.Format("{0}*{1} ", arrSrcMatrix[m, n], curPageRankMatrix[n]));
}
tgt[m] = cur;
Console.Write(string.Format("<{0}>", tgt[m]));
Console.WriteLine();
}
return tgt;
}
}
}
运算结果 c:\Users\shixun\Desktop>ConsoleApplication1.exe 0 0.03 0.455 0.455 0.03 0.455 1 0.3133333 0.03 0.03 0.03 0.03 2 0.3133333 0.03 0.03 0.88 0.455 3 0.3133333 0.03 0.03 0.03 0.03 4 0.03 0.455 0.455 0.03 0.03 Staring iteration 1... 0 0.03*0.2 0.455*0.2 0.455*0.2 0.03*0.2 0.455*0.2 <0.285> 1 0.3133333*0.2 0.03*0.2 0.03*0.2 0.03*0.2 0.03*0.2 <0.08666666> 2 0.3133333*0.2 0.03*0.2 0.03*0.2 0.88*0.2 0.455*0.2 <0.3416667> 3 0.3133333*0.2 0.03*0.2 0.03*0.2 0.03*0.2 0.03*0.2 <0.08666666> 4 0.03*0.2 0.455*0.2 0.455*0.2 0.03*0.2 0.03*0.2 <0.2> Staring iteration 2... 0 0.03*0.285 0.455*0.08666666 0.455*0.3416667 0.03*0.08666666 0.455*0.2 <0.2970417> 1 0.3133333*0.285 0.03*0.08666666 0.03*0.3416667 0.03*0.08666666 0.03*0.2 <0.11075> 2 0.3133333*0.285 0.03*0.08666666 0.03*0.3416667 0.88*0.08666666 0.455*0.2 <0.2694167> 3 0.3133333*0.285 0.03*0.08666666 0.03*0.3416667 0.03*0.08666666 0.03*0.2 <0.11075> 4 0.03*0.285 0.455*0.08666666 0.455*0.3416667 0.03*0.08666666 0.03*0.2 <0.2120417> Staring iteration 3... 0 0.03*0.2970417 0.455*0.11075 0.455*0.2694167 0.03*0.11075 0.455*0.2120417 <0.2816885> 1 0.3133333*0.2970417 0.03*0.11075 0.03*0.2694167 0.03*0.11075 0.03*0.2120417 <0.1141618> 2 0.3133333*0.2970417 0.03*0.11075 0.03*0.2694167 0.88*0.11075 0.455*0.2120417 <0.298417> 3 0.3133333*0.2970417 0.03*0.11075 0.03*0.2694167 0.03*0.11075 0.03*0.2120417 <0.1141618> 4 0.03*0.2970417 0.455*0.11075 0.455*0.2694167 0.03*0.11075 0.03*0.2120417 <0.1915708> Staring iteration 4... 0 0.03*0.2816885 0.455*0.1141618 0.455*0.298417 0.03*0.1141618 0.455*0.1915708 <0.2867636> 1 0.3133333*0.2816885 0.03*0.1141618 0.03*0.298417 0.03*0.1141618 0.03*0.1915708 <0.1098117> 2 0.3133333*0.2816885 0.03*0.1141618 0.03*0.298417 0.88*0.1141618 0.455*0.1915708 <0.2882669> 3 0.3133333*0.2816885 0.03*0.1141618 0.03*0.298417 0.03*0.1141618 0.03*0.1915708 <0.1098117> 4 0.03*0.2816885 0.455*0.1141618 0.455*0.298417 0.03*0.1141618 0.03*0.1915708 <0.205346> Staring iteration 5... 0 0.03*0.2867636 0.455*0.1098117 0.455*0.2882669 0.03*0.1098117 0.455*0.205346 <0.2864555> 1 0.3133333*0.2867636 0.03*0.1098117 0.03*0.2882669 0.03*0.1098117 0.03*0.205346 <0.1112497> 2 0.3133333*0.2867636 0.03*0.1098117 0.03*0.2882669 0.88*0.1098117 0.455*0.205346 <0.2918617> 3 0.3133333*0.2867636 0.03*0.1098117 0.03*0.2882669 0.03*0.1098117 0.03*0.205346 <0.1112497> 4 0.03*0.2867636 0.455*0.1098117 0.455*0.2882669 0.03*0.1098117 0.03*0.205346 <0.1991834> Staring iteration 6... 0 0.03*0.2864555 0.455*0.1112497 0.455*0.2918617 0.03*0.1112497 0.455*0.1991834 <0.2859753> 1 0.3133333*0.2864555 0.03*0.1112497 0.03*0.2918617 0.03*0.1112497 0.03*0.1991834 <0.1111624> 2 0.3133333*0.2864555 0.03*0.1112497 0.03*0.2918617 0.88*0.1112497 0.455*0.1991834 <0.2903775> 3 0.3133333*0.2864555 0.03*0.1112497 0.03*0.2918617 0.03*0.1112497 0.03*0.1991834 <0.1111624> 4 0.03*0.2864555 0.455*0.1112497 0.455*0.2918617 0.03*0.1112497 0.03*0.1991834 <0.2013223> Staring iteration 7... 0 0.03*0.2859753 0.455*0.1111624 0.455*0.2903775 0.03*0.1111624 0.455*0.2013223 <0.2862164> 1 0.3133333*0.2859753 0.03*0.1111624 0.03*0.2903775 0.03*0.1111624 0.03*0.2013223 <0.1110263> 2 0.3133333*0.2859753 0.03*0.1111624 0.03*0.2903775 0.88*0.1111624 0.455*0.2013223 <0.2910763> 3 0.3133333*0.2859753 0.03*0.1111624 0.03*0.2903775 0.03*0.1111624 0.03*0.2013223 <0.1110263> 4 0.03*0.2859753 0.455*0.1111624 0.455*0.2903775 0.03*0.1111624 0.03*0.2013223 <0.2006544> Staring iteration 8... 0 0.03*0.2862164 0.455*0.1110263 0.455*0.2910763 0.03*0.1110263 0.455*0.2006544 <0.2861718> 1 0.3133333*0.2862164 0.03*0.1110263 0.03*0.2910763 0.03*0.1110263 0.03*0.2006544 <0.1110946> 2 0.3133333*0.2862164 0.03*0.1110263 0.03*0.2910763 0.88*0.1110263 0.455*0.2006544 <0.2907452> 3 0.3133333*0.2862164 0.03*0.1110263 0.03*0.2910763 0.03*0.1110263 0.03*0.2006544 <0.1110946> 4 0.03*0.2862164 0.455*0.1110263 0.455*0.2910763 0.03*0.1110263 0.03*0.2006544 <0.2008936> Staring iteration 9... 0 0.03*0.2861718 0.455*0.1110946 0.455*0.2907452 0.03*0.1110946 0.455*0.2008936 <0.2861617> 1 0.3133333*0.2861718 0.03*0.1110946 0.03*0.2907452 0.03*0.1110946 0.03*0.2008936 <0.111082> 2 0.3133333*0.2861718 0.03*0.1110946 0.03*0.2907452 0.88*0.1110946 0.455*0.2008936 <0.2908922> 3 0.3133333*0.2861718 0.03*0.1110946 0.03*0.2907452 0.03*0.1110946 0.03*0.2008936 <0.111082> 4 0.03*0.2861718 0.455*0.1110946 0.455*0.2907452 0.03*0.1110946 0.03*0.2008936 <0.2007819> Staring iteration 10... 0 0.03*0.2861617 0.455*0.111082 0.455*0.2908922 0.03*0.111082 0.455*0.2007819 <0.2861714> 1 0.3133333*0.2861617 0.03*0.111082 0.03*0.2908922 0.03*0.111082 0.03*0.2007819 <0.1110791> 2 0.3133333*0.2861617 0.03*0.111082 0.03*0.2908922 0.88*0.111082 0.455*0.2007819 <0.2908311> 3 0.3133333*0.2861617 0.03*0.111082 0.03*0.2908922 0.03*0.111082 0.03*0.2007819 <0.1110791> 4 0.03*0.2861617 0.455*0.111082 0.455*0.2908922 0.03*0.111082 0.03*0.2007819 <0.200839> Staring iteration 11... 0 0.03*0.2861714 0.455*0.1110791 0.455*0.2908311 0.03*0.1110791 0.455*0.200839 <0.2861685> 1 0.3133333*0.2861714 0.03*0.1110791 0.03*0.2908311 0.03*0.1110791 0.03*0.200839 <0.1110819> 2 0.3133333*0.2861714 0.03*0.1110791 0.03*0.2908311 0.88*0.1110791 0.455*0.200839 <0.2908558> 3 0.3133333*0.2861714 0.03*0.1110791 0.03*0.2908311 0.03*0.1110791 0.03*0.200839 <0.1110819> 4 0.03*0.2861714 0.455*0.1110791 0.455*0.2908311 0.03*0.1110791 0.03*0.200839 <0.2008119> Staring iteration 12... 0 0.03*0.2861685 0.455*0.1110819 0.455*0.2908558 0.03*0.1110819 0.455*0.2008119 <0.2861685> 1 0.3133333*0.2861685 0.03*0.1110819 0.03*0.2908558 0.03*0.1110819 0.03*0.2008119 <0.1110811> 2 0.3133333*0.2861685 0.03*0.1110819 0.03*0.2908558 0.88*0.1110819 0.455*0.2008119 <0.2908457> 3 0.3133333*0.2861685 0.03*0.1110819 0.03*0.2908558 0.03*0.1110819 0.03*0.2008119 <0.1110811> 4 0.03*0.2861685 0.455*0.1110819 0.455*0.2908558 0.03*0.1110819 0.03*0.2008119 <0.2008235> Staring iteration 13... 0 0.03*0.2861685 0.455*0.1110811 0.455*0.2908457 0.03*0.1110811 0.455*0.2008235 <0.2861689> 1 0.3133333*0.2861685 0.03*0.1110811 0.03*0.2908457 0.03*0.1110811 0.03*0.2008235 <0.1110811> 2 0.3133333*0.2861685 0.03*0.1110811 0.03*0.2908457 0.88*0.1110811 0.455*0.2008235 <0.29085> 3 0.3133333*0.2861685 0.03*0.1110811 0.03*0.2908457 0.03*0.1110811 0.03*0.2008235 <0.1110811> 4 0.03*0.2861685 0.455*0.1110811 0.455*0.2908457 0.03*0.1110811 0.03*0.2008235 <0.2008189>