程序员编程艺术第二十三~四章：杨氏矩阵查找，倒排索引关键词Hash编码

  第二十三、四章：杨氏矩阵查找，倒排索引关键词Hash不重复编码实践

作者：July、yansha。编程艺术室出品。
出处：结构之法算法之道。

前言

    本文阐述两个问题，第三十三章是杨氏矩阵查找问题，第三十四章是有关倒排索引中关键词Hash编码的问题，主要要解决不重复以及追加的功能，同时也是经典算法研究系列十一、从头到尾彻底解析Hash表算法之续。

    OK，有任何问题，也欢迎随时交流或批评指正。谢谢。

第二十三章、杨氏矩阵查找

杨氏矩阵查找

    先看一个来自算法导论习题里6-3与剑指offer的一道编程题（也被经常用作面试题，本人此前去搜狗二面时便遇到了）：

    在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
    例如下面的二维数组就是每行、每列都递增排序。如果在这个数组中查找数字6，则返回true；如果查找数字5，由于数组不含有该数字，则返回false。

    本Young问题解法有二（如查找数字6）：

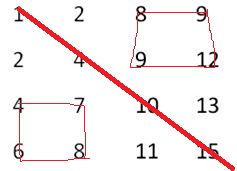
    1、分治法，分为四个矩形，配以二分查找，如果要找的数是6介于对角线上相邻的两个数4、10，可以排除掉左上和右下的两个矩形，而递归在左下和右上的两个矩形继续找，如下图所示：

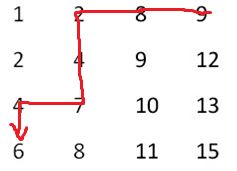
    2、首先直接定位到最右上角的元素，再配以二分查找，比要找的数（6）大就往左走，比要找数（6）的小就往下走，直到找到要找的数字（6）为止，如下图所示：

    上述方法二的关键代码+程序运行如下图所示：

    试问，上述算法复杂么？不复杂，只要稍微动点脑筋便能想到，还可以参看友人老梦的文章，Young氏矩阵：http://blog.csdn.net/zhanglei8893/article/details/6234564，以及IT练兵场的：http://www.jobcoding.com/array/matrix/young-tableau-problem/，除此之外，何海涛先生一书剑指offer中也收集了此题，感兴趣的朋友也可以去看看。

第三十四章、经典算法十一Hash表算法（续）、倒排索引关键词不重复Hash编码 

    本章要介绍这样一个问题，对倒排索引中的关键词进行编码。那么，这个问题将分为两个个步骤：

1. 首先，要提取倒排索引内词典文件中的关键词；
2. 对提取出来的关键词进行编码。本章采取hash编码的方式。既然要用hash编码，那么最重要的就是要解决hash冲突的问题，下文会详细介绍。

    有一点必须提醒读者的是，倒排索引包含词典和倒排记录表两个部分，词典一般有词项（或称为关键词）和词项频率（即这个词项或关键词出现的次数），倒排记录表则记录着上述词项（或关键词）所出现的位置，或出现的文档及网页ID等相关信息。

34.1、正排索引与倒排索引  

    咱们先来看什么是倒排索引，以及倒排索引与正排索引之间的区别：

    我们知道，搜索引擎的关键步骤就是建立倒排索引，所谓倒排索引一般表示为一个关键词，然后是它的频度（出现的次数），位置（出现在哪一篇文章或网页中，及有关的日期，作者等信息），它相当于为互联网上几千亿页网页做了一个索引，好比一本书的目录、标签一般。读者想看哪一个主题相关的章节，直接根据目录即可找到相关的页面。不必再从书的第一页到最后一页，一页一页的查找。

    接下来，阐述下正排索引与倒排索引的区别：

一般索引（正排索引）     

    正排表是以文档的ID为关键字，表中记录文档中每个字的位置信息，查找时扫描表中每个文档中字的信息直到找出所有包含查询关键字的文档。正排表结构如图1所示，这种组织方法在建立索引的时候结构比较简单，建立比较方便且易于维护;因为索引是基于文档建立的，若是有新的文档假如，直接为该文档建立一个新的索引块，挂接在原来索引文件的后面。若是有文档删除，则直接找到该文档号文档对因的索引信息，将其直接删除。但是在查询的时候需对所有的文档进行扫描以确保没有遗漏，这样就使得检索时间大大延长，检索效率低下。      

    尽管正排表的工作原理非常的简单，但是由于其检索效率太低，除非在特定情况下，否则实用性价值不大。 

倒排索引

    倒排表以字或词为关键字进行索引，表中关键字所对应的记录表项记录了出现这个字或词的所有文档，一个表项就是一个字表段，它记录该文档的ID和字符在该文档中出现的位置情况。由于每个字或词对应的文档数量在动态变化，所以倒排表的建立和维护都较为复杂，但是在查询的时候由于可以一次得到查询关键字所对应的所有文档，所以效率高于正排表。在全文检索中，检索的快速响应是一个最为关键的性能，而索引建立由于在后台进行，尽管效率相对低一些，但不会影响整个搜索引擎的效率。

    倒排表的结构图如图2： 

    倒排表的索引信息保存的是字或词后继数组模型、互关联后继数组模型条在文档内的位置，在同一篇文档内相邻的字或词条的前后关系没有被保存到索引文件内。

34.2、倒排索引中提取关键词

    倒排索引是搜索引擎之基石。建成了倒排索引后，用户要查找某个query，如在搜索框输入某个关键词：“结构之法”后，搜索引擎不会再次使用爬虫又一个一个去抓取每一个网页，从上到下扫描网页，看这个网页有没有出现这个关键词，而是会在它预先生成的倒排索引文件中查找和匹配包含这个关键词“结构之法”的所有网页。找到了之后，再按相关性度排序，最终把排序后的结果显示给用户。

    如下，即是一个倒排索引文件（不全），我们把它取名为big_index，文件中每一较短的，不包含有“#####”符号的便是某个关键词，及这个关键词的出现次数。现在要从这个大索引文件中提取出这些关键词，--Firelf--，-11，-Winter-，.，007，007：天降杀机，02Chan..如何做到呢？一行一行的扫描整个索引文件么？

    何意？之前已经说过：倒排索引包含词典和倒排记录表两个部分，词典一般有词项（或称为关键词）和词项频率（即这个词项或关键词出现的次数），倒排记录表则记录着上述词项（或关键词）所出现的位置，或出现的文档及网页ID等相关信息。

    最简单的讲，就是要提取词典中的词项（关键词）：--Firelf--，-11，-Winter-，.，007，007：天降杀机，02Chan...。

--Firelf--（关键词） 8（出现次数）

    我们可以试着这么解决：通过查找#####便可判断某一行出现的词是不是关键词，但如果这样做的话，便要扫描整个索引文件的每一行，代价实在巨大。如何提高速度呢？对了，关键词后面的那个出现次数为我们问题的解决起到了很好的作用，如下注释所示：

//  本身没有##### 的行判定为关键词行，后跟这个关键词的行数N（即词项频率）
//  接下来，截取关键词--Firelf--，然后读取后面关键词的行数N
//  再跳过N行（滤过和避免扫描中间的倒排记录表信息）
//  读取下一个关键词..

    有朋友指出，上述方法虽然减少了扫描的行数，但并没有减少I0开销。读者是否有更好地办法？欢迎随时交流。

34.2、为提取出来的关键词编码

    爱思考的朋友可能会问，上述从倒排索引文件中提取出那些关键词（词项）的操作是为了什么呢？其实如我个人微博上12月12日所述的Hash词典编码：

    词典文件的编码：1、词典怎么生成（存储和构造词典）；2、如何运用hash对输入的汉字进行编码；3、如何更好的解决冲突，即不重复以及追加功能。具体例子为：事先构造好词典文件后，输入一个词，要求找到这个词的编码，然后将其编码输出。且要有不断能添加词的功能，不得重复。
    步骤应该是如下：1、读索引文件；2、提取索引中的词出来；3、词典怎么生成，存储和构造词典；4、词典文件的编码：不重复与追加功能。编码比如，输入中国，他的编码可以为10001，然后输入银行，他的编码可以为10002。只要实现不断添加词功能，以及不重复即可，词典类的大文件，hash最重要的是怎样避免冲突。

    也就是说，现在我要对上述提取出来后的关键词进行编码，采取何种方式编码呢？暂时用hash函数编码。编码之后的效果将是每一个关键词都有一个特定的编码，如下图所示（与上文big_index文件比较一下便知）：

    --Firelf--  对应编码为：135942

    -11         对应编码为：106101

    ....

    但细心的朋友一看上图便知，其中第34~39行显示，有重复的编码，那么如何解决这个不重复编码的问题呢？

34.3、暴雪的Hash算法

    值得一提的是，在解决Hash冲突的时候，搞的焦头烂额，结果今天上午在自己的博客内的一篇文章（十一、从头到尾彻底解析Hash表算法）内找到了解决办法：网上流传甚广的暴雪的Hash算法。咱们再来回顾下：

“接下来，咱们来具体分析一下一个最快的Hash表算法。
我们由一个简单的问题逐步入手：有一个庞大的字符串数组，然后给你一个单独的字符串，让你从这个数组中查找是否有这个字符串并找到它，你会怎么做？
有一个方法最简单，老老实实从头查到尾，一个一个比较，直到找到为止，我想只要学过程序设计的人都能把这样一个程序作出来，但要是有程序员把这样的程序交给用户，我只能用无语来评价，或许它真的能工作，但...也只能如此了。
最合适的算法自然是使用HashTable（哈希表），先介绍介绍其中的基本知识，所谓Hash，一般是一个整数，通过某种算法，可以把一个字符串"压缩" 成一个整数。当然，无论如何，一个32位整数是无法对应回一个字符串的，但在程序中，两个字符串计算出的Hash值相等的可能非常小，下面看看在MPQ中的Hash算法：
    函数prepareCryptTable以下的函数生成一个长度为0x500（合10进制数：1280）的cryptTable[0x500]

//函数prepareCryptTable以下的函数生成一个长度为0x500（合10进制数：1280）的cryptTable[0x500] void prepareCryptTable() { unsigned long seed = 0x00100001, index1 = 0, index2 = 0, i; for( index1 = 0; index1 < 0x100; index1++ ) { for( index2 = index1, i = 0; i < 5; i++, index2 += 0x100 ) { unsigned long temp1, temp2; seed = (seed * 125 + 3) % 0x2AAAAB; temp1 = (seed & 0xFFFF) << 0x10; seed = (seed * 125 + 3) % 0x2AAAAB; temp2 = (seed & 0xFFFF); cryptTable[index2] = ( temp1 | temp2 ); } } }

    函数HashString以下函数计算lpszFileName 字符串的hash值，其中dwHashType 为hash的类型，

//函数HashString以下函数计算lpszFileName 字符串的hash值，其中dwHashType 为hash的类型， unsigned long HashString(const char *lpszkeyName, unsigned long dwHashType ) { unsigned char *key = (unsigned char *)lpszkeyName; unsigned long seed1 = 0x7FED7FED; unsigned long seed2 = 0xEEEEEEEE; int ch; while( *key != 0 ) { ch = *key++; seed1 = cryptTable[(dwHashType<<8) + ch] ^ (seed1 + seed2); seed2 = ch + seed1 + seed2 + (seed2<<5) + 3; } return seed1; }

    Blizzard的这个算法是非常高效的，被称为"One-Way Hash"( A one-way hash is a an algorithm that is constructed in such a way that deriving the original string (set of strings, actually) is virtually impossible)。举个例子，字符串"unitneutralacritter.grp"通过这个算法得到的结果是0xA26067F3。
　是不是把第一个算法改进一下，改成逐个比较字符串的Hash值就可以了呢，答案是，远远不够，要想得到最快的算法，就不能进行逐个的比较，通常是构造一个哈希表(Hash Table)来解决问题，哈希表是一个大数组，这个数组的容量根据程序的要求来定义，
     例如1024，每一个Hash值通过取模运算 (mod) 对应到数组中的一个位置，这样，只要比较这个字符串的哈希值对应的位置有没有被占用，就可以得到最后的结果了，想想这是什么速度？是的，是最快的O(1)，现在仔细看看这个算法吧：
typedef struct { int nHashA; int nHashB; char bExists; ...... } SOMESTRUCTRUE; //一种可能的结构体定义？    函数GetHashTablePos下述函数为在Hash表中查找是否存在目标字符串，有则返回要查找字符串的Hash值，无则，return -1.
//函数GetHashTablePos下述函数为在Hash表中查找是否存在目标字符串，有则返回要查找字符串的Hash值，无则，return -1. int GetHashTablePos( har *lpszString, SOMESTRUCTURE *lpTable ) //lpszString要在Hash表中查找的字符串，lpTable为存储字符串Hash值的Hash表。 { int nHash = HashString(lpszString); //调用上述函数HashString，返回要查找字符串lpszString的Hash值。 int nHashPos = nHash % nTableSize; if ( lpTable[nHashPos].bExists && !strcmp( lpTable[nHashPos].pString, lpszString ) ) { //如果找到的Hash值在表中存在，且要查找的字符串与表中对应位置的字符串相同， return nHashPos; //返回找到的Hash值 } else { return -1; } }    看到此，我想大家都在想一个很严重的问题：“如果两个字符串在哈希表中对应的位置相同怎么办？”,毕竟一个数组容量是有限的，这种可能性很大。解决该问题的方法很多，我首先想到的就是用“链表”,感谢大学里学的数据结构教会了这个百试百灵的法宝，我遇到的很多算法都可以转化成链表来解决，只要在哈希表的每个入口挂一个链表，保存所有对应的字符串就OK了。事情到此似乎有了完美的结局，如果是把问题独自交给我解决，此时我可能就要开始定义数据结构然后写代码了。
    然而Blizzard的程序员使用的方法则是更精妙的方法。基本原理就是：他们在哈希表中不是用一个哈希值而是用三个哈希值来校验字符串。 ”

    “MPQ使用文件名哈希表来跟踪内部的所有文件。但是这个表的格式与正常的哈希表有一些不同。首先，它没有使用哈希作为下标，把实际的文件名存储在表中用于验证，实际上它根本就没有存储文件名。而是使用了3种不同的哈希：一个用于哈希表的下标，两个用于验证。这两个验证哈希替代了实际文件名。
    当然了，这样仍然会出现2个不同的文件名哈希到3个同样的哈希。但是这种情况发生的概率平均是：1:18889465931478580854784，这个概率对于任何人来说应该都是足够小的。现在再回到数据结构上，Blizzard使用的哈希表没有使用链表，而采用"顺延"的方式来解决问题。 ”下面，咱们来看看这个网上流传甚广的暴雪hash算法：
    函数GetHashTablePos中，lpszString 为要在hash表中查找的字符串；lpTable 为存储字符串hash值的hash表；nTableSize 为hash表的长度： 
//函数GetHashTablePos中，lpszString 为要在hash表中查找的字符串；lpTable 为存储字符串hash值的hash表；nTableSize 为hash表的长度： int GetHashTablePos( char *lpszString, MPQHASHTABLE *lpTable, int nTableSize ) { const int HASH_OFFSET = 0, HASH_A = 1, HASH_B = 2; int nHash = HashString( lpszString, HASH_OFFSET ); int nHashA = HashString( lpszString, HASH_A ); int nHashB = HashString( lpszString, HASH_B ); int nHashStart = nHash % nTableSize; int nHashPos = nHashStart; while ( lpTable[nHashPos].bExists ) { // 如果仅仅是判断在该表中时候存在这个字符串，就比较这两个hash值就可以了，不用对结构体中的字符串进行比较。 // 这样会加快运行的速度？减少hash表占用的空间？这种方法一般应用在什么场合？ if ( 　 lpTable[nHashPos].nHashA == nHashA && lpTable[nHashPos].nHashB == nHashB ) { return nHashPos; } else { nHashPos = (nHashPos + 1) % nTableSize; } if (nHashPos == nHashStart) break; } return -1; }

    上述程序解释：

1. 计算出字符串的三个哈希值（一个用来确定位置，另外两个用来校验)
2. 察看哈希表中的这个位置
3. 哈希表中这个位置为空吗？如果为空，则肯定该字符串不存在，返回-1。
4. 如果存在，则检查其他两个哈希值是否也匹配，如果匹配，则表示找到了该字符串，返回其Hash值。
5. 移到下一个位置，如果已经移到了表的末尾，则反绕到表的开始位置起继续查询　
6. 看看是不是又回到了原来的位置，如果是，则返回没找到
7. 回到3。

34.4、不重复Hash编码

    有了上面的暴雪Hash算法。咱们的问题便可解决了。不过，有两点必须先提醒读者：1、Hash表起初要初始化；2、暴雪的Hash算法对于查询那样处理可以，但对插入就不能那么解决。

    关键主体代码如下：

//函数prepareCryptTable以下的函数生成一个长度为0x500（合10进制数：1280）的cryptTable[0x500] void prepareCryptTable() { unsigned long seed = 0x00100001, index1 = 0, index2 = 0, i; for( index1 = 0; index1 <0x100; index1++ ) { for( index2 = index1, i = 0; i < 5; i++, index2 += 0x100) { unsigned long temp1, temp2; seed = (seed * 125 + 3) % 0x2AAAAB; temp1 = (seed & 0xFFFF)<<0x10; seed = (seed * 125 + 3) % 0x2AAAAB; temp2 = (seed & 0xFFFF); cryptTable[index2] = ( temp1 | temp2 ); } } } //函数HashString以下函数计算lpszFileName 字符串的hash值，其中dwHashType 为hash的类型， unsigned long HashString(const char *lpszkeyName, unsigned long dwHashType ) { unsigned char *key = (unsigned char *)lpszkeyName; unsigned long seed1 = 0x7FED7FED; unsigned long seed2 = 0xEEEEEEEE; int ch; while( *key != 0 ) { ch = *key++; seed1 = cryptTable[(dwHashType<<8) + ch] ^ (seed1 + seed2); seed2 = ch + seed1 + seed2 + (seed2<<5) + 3; } return seed1; } ///////////////////////////////////////////////////////////////////// //function: 哈希词典 编码 //parameter: //author: lei.zhou //time: 2011-12-14 ///////////////////////////////////////////////////////////////////// MPQHASHTABLE TestHashTable[nTableSize]; int TestHashCTable[nTableSize]; int TestHashDTable[nTableSize]; key_list test_data[nTableSize]; //直接调用上面的hashstring，nHashPos就是对应的HASH值。 int insert_string(const char *string_in) { const int HASH_OFFSET = 0, HASH_C = 1, HASH_D = 2; unsigned int nHash = HashString(string_in, HASH_OFFSET); unsigned int nHashC = HashString(string_in, HASH_C); unsigned int nHashD = HashString(string_in, HASH_D); unsigned int nHashStart = nHash % nTableSize; unsigned int nHashPos = nHashStart; int ln, ires = 0; while (TestHashTable[nHashPos].bExists) { // if (TestHashCTable[nHashPos] == (int) nHashC && TestHashDTable[nHashPos] == (int) nHashD) // break; // //... // else //如之前所提示读者的那般，暴雪的Hash算法对于查询那样处理可以，但对插入就不能那么解决 nHashPos = (nHashPos + 1) % nTableSize; if (nHashPos == nHashStart) break; } ln = strlen(string_in); if (!TestHashTable[nHashPos].bExists && (ln < nMaxStrLen)) { TestHashCTable[nHashPos] = nHashC; TestHashDTable[nHashPos] = nHashD; test_data[nHashPos] = (KEYNODE *) malloc (sizeof(KEYNODE) * 1); if(test_data[nHashPos] == NULL) { printf("10000 EMS ERROR !!!!\n"); return 0; } test_data[nHashPos]->pkey = (char *)malloc(ln+1); if(test_data[nHashPos]->pkey == NULL) { printf("10000 EMS ERROR !!!!\n"); return 0; } memset(test_data[nHashPos]->pkey, 0, ln+1); strncpy(test_data[nHashPos]->pkey, string_in, ln); *((test_data[nHashPos]->pkey)+ln) = 0; test_data[nHashPos]->weight = nHashPos; TestHashTable[nHashPos].bExists = 1; } else { if(TestHashTable[nHashPos].bExists) printf("30000 in the hash table %s !!!\n", string_in); else printf("90000 strkey error !!!\n"); } return nHashPos; }

    接下来要读取索引文件big_index对其中的关键词进行编码（为了简单起见，直接一行一行扫描读写，没有跳过行数了）：

void bigIndex_hash(const char *docpath, const char *hashpath) { FILE *fr, *fw; int len; char *pbuf, *p; char dockey[TERM_MAX_LENG]; if(docpath == NULL || *docpath == '\0') return; if(hashpath == NULL || *hashpath == '\0') return; fr = fopen(docpath, "rb"); //读取文件docpath fw = fopen(hashpath, "wb"); if(fr == NULL || fw == NULL) { printf("open read or write file error!\n"); return; } pbuf = (char*)malloc(BUFF_MAX_LENG); if(pbuf == NULL) { fclose(fr); return ; } memset(pbuf, 0, BUFF_MAX_LENG); while(fgets(pbuf, BUFF_MAX_LENG, fr)) { len = GetRealString(pbuf); if(len <= 1) continue; p = strstr(pbuf, "#####"); if(p != NULL) continue; p = strstr(pbuf, " "); if (p == NULL) { printf("file contents error!"); } len = p - pbuf; dockey[0] = 0; strncpy(dockey, pbuf, len); dockey[len] = 0; int num = insert_string(dockey); dockey[len] = ' '; dockey[len+1] = '\0'; char str[20]; itoa(num, str, 10); strcat(dockey, str); dockey[len+strlen(str)+1] = '\0'; fprintf (fw, "%s\n", dockey); } free(pbuf); fclose(fr); fclose(fw); }

    主函数已经很简单了，如下：

int main() { prepareCryptTable(); //Hash表起初要初始化 //现在要把整个big_index文件插入hash表，以取得编码结果 bigIndex_hash("big_index.txt", "hashpath.txt"); system("pause"); return 0; }

    程序运行后生成的hashpath.txt文件如下：

    如上所示，采取暴雪的Hash算法并在插入的时候做适当处理，当再次对上文中的索引文件big_index进行Hash编码后，冲突问题已经得到初步解决。当然，还有待更进一步更深入的测试。

后续添上数目索引1~10000...

    后来又为上述文件中的关键词编了码一个计数的内码，不过，奇怪的是，同样的代码，在Dev C++ 与VS2010上运行结果却不同（左边dev上计数从"1"开始，VS上计数从“1994014002”开始），如下图所示：

    在上面的bigIndex_hashcode函数的基础上，修改如下，即可得到上面的效果：

void bigIndex_hashcode(const char *in_file_path, const char *out_file_path) { FILE *fr, *fw; int len, value; char *pbuf, *pleft, *p; char keyvalue[TERM_MAX_LENG], str[WORD_MAX_LENG]; if(in_file_path == NULL || *in_file_path == '\0') { printf("input file path error!\n"); return; } if(out_file_path == NULL || *out_file_path == '\0') { printf("output file path error!\n"); return; } fr = fopen(in_file_path, "r"); //读取in_file_path路径文件 fw = fopen(out_file_path, "w"); if(fr == NULL || fw == NULL) { printf("open read or write file error!\n"); return; } pbuf = (char*)malloc(BUFF_MAX_LENG); pleft = (char*)malloc(BUFF_MAX_LENG); if(pbuf == NULL || pleft == NULL) { printf("allocate memory error!"); fclose(fr); return ; } memset(pbuf, 0, BUFF_MAX_LENG); int offset = 1; while(fgets(pbuf, BUFF_MAX_LENG, fr)) { if (--offset > 0) continue; if(GetRealString(pbuf) <= 1) continue; p = strstr(pbuf, "#####"); if(p != NULL) continue; p = strstr(pbuf, " "); if (p == NULL) { printf("file contents error!"); } len = p - pbuf; // 确定跳过行数 strcpy(pleft, p+1); offset = atoi(pleft) + 1; strncpy(keyvalue, pbuf, len); keyvalue[len] = '\0'; value = insert_string(keyvalue); if (value != -1) { // key value中插入空格 keyvalue[len] = ' '; keyvalue[len+1] = '\0'; itoa(value, str, 10); strcat(keyvalue, str); keyvalue[len+strlen(str)+1] = ' '; keyvalue[len+strlen(str)+2] = '\0'; keysize++; itoa(keysize, str, 10); strcat(keyvalue, str); // 将key value写入文件 fprintf (fw, "%s\n", keyvalue); } } free(pbuf); fclose(fr); fclose(fw); }

小结

    本文有一点值得一提的是，在此前的这篇文章（十一、从头到尾彻底解析Hash表算法）之中，只是对Hash表及暴雪的Hash算法有过学习和了解，但尚未真正运用过它，而今在本章中体现，证明还是之前写的文章，及之前对Hash表等算法的学习还是有一定作用的。同时，也顺便对暴雪的Hash函数算是做了个测试，其的确能解决一般的冲突性问题，创造这个算法的人不简单呐。

后记

    再次感谢老大xiaoqi，以及艺术室内朋友xiaolin，555，yansha的指导。没有他们的帮助，我将寸步难行。日后，自己博客内的文章要经常回顾，好好体会。同时，写作本文时，刚接触倒排索引等相关问题不久，若有任何问题，欢迎随时交流或批评指正。

    最后，基于本blog的分为程序语言，数据结构，算法讨论，面试题库，编程技巧五大板块交流的论坛正在加紧建设当中（总负责人：scott && yinhex && 网络骑士），相信不久以后便会与大家见面。谢谢。 完。