poj 2464 Brownie Points II （扫描线）

题意：在平面直角坐标系中给你N个点，stan和ollie玩一个游戏，首先stan在竖直方向上画一条直线，该直线必须要过其中的某个点，然后ollie在水平方向上画一条直线，该直线的要求是要经过一个stan之前画过的点。 这时候平面就被分割成了四块，两个人这时候会有一个得分，stan的得分是平面上第1、3象限内的点的个数，ollie的得分是平面上第2、4象限内的点的个数，在统计的时候在所画线上的点都不计算在内。求最终stan使得自己的最差得分最高，并且输出此时ollie的得分。

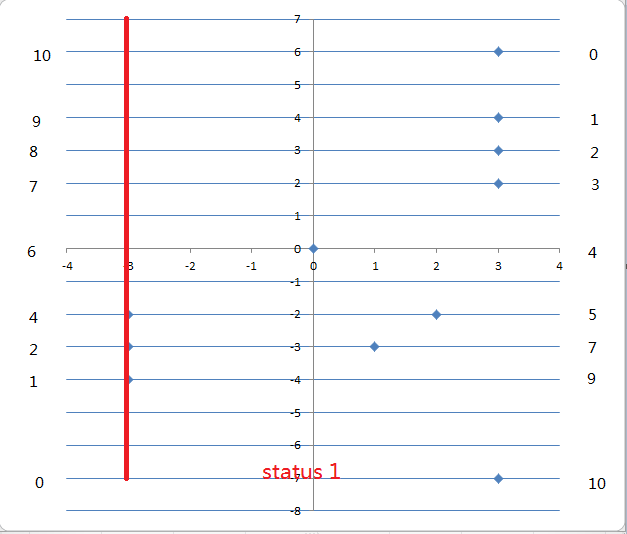
        根据题目中的数据画出来的图是这样的，两边的数字分别表示的是，低于当前点y坐标的点的个数（用ol[]数组表示），高于当前点y坐标的点的个数（用st[]数组表示），分别用这两个数组建两棵线段树，表示Ollie的分数和stan的分数。处理出这样的数据后，我们把坐标以x从小到大排序，之后，每扫到一个x即是stan画下了一条竖线，这时候，Ollie画下的横线就是每个扫到的点的y坐标。

        在status 1的时候，当Ollie取的横线分别是y=-4、-3、-2时，stan的分数分别是st[-4]=9，st[-3]=7和st[-2]=5，而Ollie的分数分别是ol[-4]=1，ol[-3]=2和ol[-2]=4。（即分别在线段树里单点查询这些点的值）

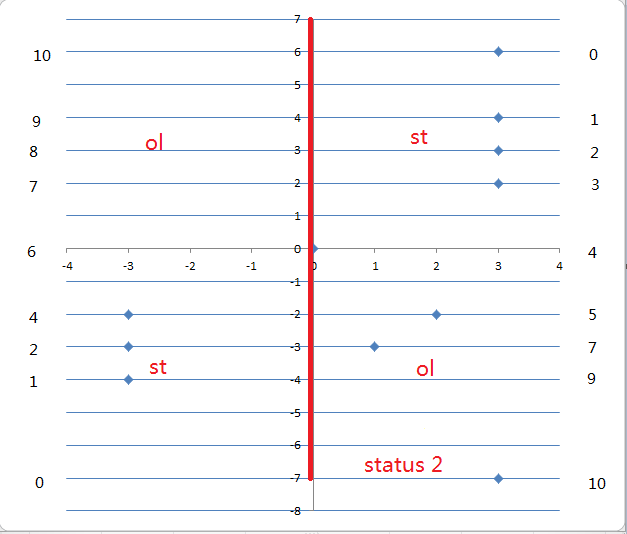
当扫第x=0的时候，原来属于Ollie的3个点，即(-3,-4)，(-3,-3)，(-3,-3)已经是属于stan，这怎么在线段树里体现里？当这时候，当Ollie选择横线的y是大于等于-3的时候，那么(-3,-4)是点是属于stan的，那么我们就可以在stan的线段树里在区间[-3，7]里加1（这就搞定了不是？），同理处理出(-3,-3)，(-3,-2)，而Ollie得分的处理方式是类似的，这样的处理可以在status 1里完成，所以当我们到达status 2的时候，只需要处理(0,0)这个点，之后，那么我们在两棵线段树里分别查询y=0，即得到了在status 2时stan和Ollie的分数。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;

#define LL(x) (x<<1)
#define RR(x) (x<<1|1)
#define MID(a,b) (a+((b-a)>>1))
const int N=200005;

struct Point
{
	int x,y;
	void get(){scanf("%d%d",&x,&y);}
	bool operator<(const Point&b)const
	{ return x<b.x; }
}p[N];
struct node
{
	int lft,rht;
	int flag[2];
	int mid(){return MID(lft,rht);}
	void init(int a,int b)
	{
		flag[0]=a;	flag[1]=b;
	}
};

int n,m,mi;
vector<int> mx;
map<int,int> H;
int y[N],st[N],ol[N];

struct Segtree
{
	node tree[N*4];
	void down(int ind)
	{
		for(int i=0;i<2;i++)
		{
			tree[LL(ind)].flag[i]+=tree[ind].flag[i];
			tree[RR(ind)].flag[i]+=tree[ind].flag[i];
			tree[ind].flag[i]=0;
		}
	}
	void build(int lft,int rht,int ind)
	{
		tree[ind].lft=lft;	tree[ind].rht=rht;
		tree[ind].init(0,0);	
		if(lft==rht) tree[ind].init(st[lft],ol[lft]);
		else
		{
			int mid=tree[ind].mid();
			build(lft,mid,LL(ind));
			build(mid+1,rht,RR(ind));
		}
	}
	void updata(int st,int ed,int ind,int type,int valu)
	{
		int lft=tree[ind].lft,rht=tree[ind].rht;
		if(st<=lft&&rht<=ed) tree[ind].flag[type]+=valu;
		else 
		{	
			down(ind);
			int mid=tree[ind].mid();
			if(st<=mid) updata(st,ed,LL(ind),type,valu);
			if(ed> mid) updata(st,ed,RR(ind),type,valu);
		}
	}
	void query(int pos,int ind,int &mi,int &mx)
	{
		if(tree[ind].lft==tree[ind].rht) 
		{
			mi=tree[ind].flag[0];
			mx=tree[ind].flag[1];
		}
		else 
		{
			down(ind);
			int mid=tree[ind].mid();
			if(pos<=mid) return query(pos,LL(ind),mi,mx);
			if(pos> mid) return query(pos,RR(ind),mi,mx);
		}
	}
}seg;
int main()
{
	while(scanf("%d",&n),n)
	{
		H.clear(); mx.clear(); mi=m=0;

		int id1=0,id2=0;
		for(int i=0;i<n;i++)
		{
			p[i].get();
			y[i]=p[i].y;
		}
		sort(y,y+n);	sort(p,p+n);
		H[y[0]]=0;
		for(int i=0;i<n;i++)
		{
			if(y[m]!=y[i])
			{
				st[m]=n-i;
				y[++m]=y[i];
				ol[m]=i;
				H[y[m]]=m;
			}
		}
		st[m]=0;
		seg.build(0,m,1);
		while(id1<n)
		{
			id2=id1;
			while(p[id1].x==p[id2].x)
			{
				if(p[id2].y!=y[0]) seg.updata(H[y[0]],H[p[id2].y]-1,1,0,-1);
				if(p[id2].y!=y[m]) seg.updata(H[p[id2].y]+1,H[y[m]],1,1,-1);
				if(++id2>=n) break;
			}
			int mii=n,mxx=0;
			for(int i=id1;i<id2;i++)
			{
				int tmp1,tmp2;
				seg.query(H[p[i].y],1,tmp1,tmp2);
				mii=min(mii,tmp1);
				mxx=max(mxx,tmp2);
			}
			if(mii==mi) mx.push_back(mxx);
			else if(mii>mi)
			{
				mi=mii;
				mx.clear(); mx.push_back(mxx);
			}
			for(int i=id1;i<id2;i++)
			{
				if(p[i].y!=y[0]) seg.updata(H[y[0]],H[p[i].y]-1,1,1,1);
				if(p[i].y!=y[m]) seg.updata(H[p[i].y]+1,H[y[m]],1,0,1);
			}
			id1=id2;
		}
		sort(mx.begin(),mx.end());
		mx.erase(unique(mx.begin(),mx.end()),mx.end());
		printf("Stan: %d; Ollie:",mi);
		for(int i=0;i<(int)mx.size();i++) printf(" %d",mx[i]);
		printf(";\n");
	}
	return 0;
}