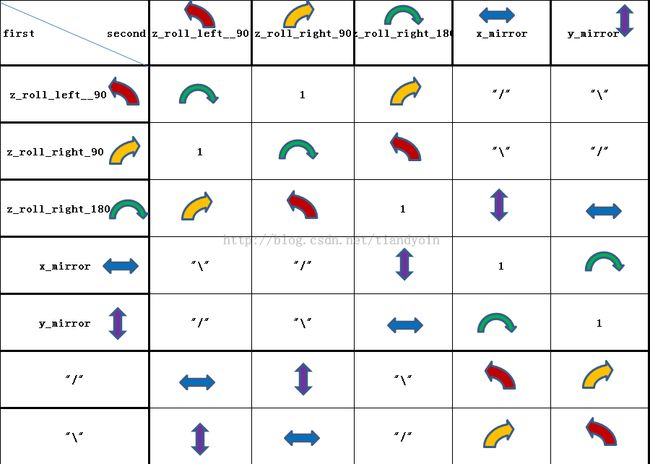
平面旋转的折叠定理
上面的表
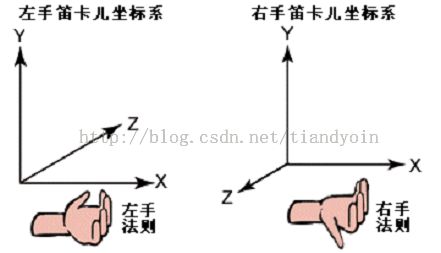
采用“右手笛卡儿坐标系”,但是把Z轴翻过来,Z轴正方向为屏幕从外向里。
平面上的顺时针旋转90度,是相对于Z轴, 右(手)旋(转)90度,和“安培右手守则”一个道理。
平面上的逆时针旋转90度,是相对于Z轴, 左(手)旋(转)90度,
平面上的逆时针旋转180度,是相对于Z轴, 右(手)旋(转)180度,
平面上的水平方向上镜像,是相对于Y轴,右(手)旋(转)180度,
平面上的竖直方向上镜像,是相对于X轴,右(手)旋(转)180度,
可以看出以上的变换都是做旋转,定义成如下:
enum {
z_roll_left__90; // 逆时针90度
z_roll_right_90; // 顺时针90度
z_roll_right_180; // 旋转180度
x_mirror = y_roll_right_180; // 水平方向上镜像
y_mirror = x_roll_right_180; // 竖直方向上镜像
};
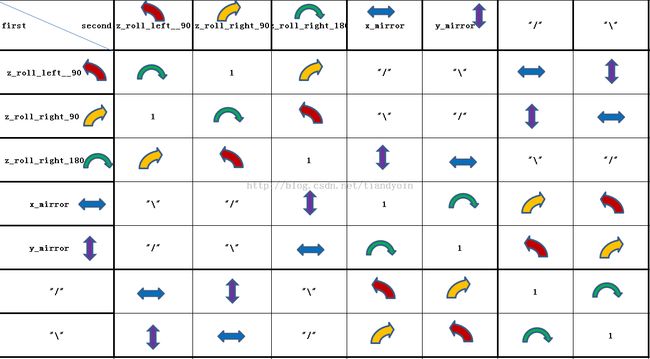
折叠原理(适合结合律,不适合交换律),$x表示单位x正向量:
"/" = 平面以"/"对角线镜像,以$x-$y轴, 右(手)旋(转)180度
"\" = 平面以"\"对角线镜像,以$y-$x轴, 右(手)旋(转)180度
折叠原理(适合结合律,不适合交换律),$x表示单位x正向量:
-----------------------------------------------------
z_roll_left__90 && z_roll_left__90 = z_roll_right_180;
z_roll_left__90 && z_roll_right_90 = 1;
z_roll_left__90 && z_roll_right_180 = z_roll_right_90;
z_roll_left__90 && x_mirror = 平面以"/"对角线镜像,以$x-$y轴, 右(手)旋(转)180度
z_roll_left__90 && y_mirror = 平面以"\"对角线镜像,以$y-$x轴, 右(手)旋(转)180度
z_roll_right_90 && z_roll_left__90 = 1;
z_roll_right_90 && z_roll_right_90 = z_roll_right_180;
z_roll_right_90 && z_roll_right_180 = z_roll_left__90;
z_roll_right_90 && x_mirror = 平面以"\"对角线镜像,以$y-$x轴, 右(手)旋(转)180度
z_roll_right_90 && y_mirror = 平面以"/"对角线镜像,以$x-$y轴, 右(手)旋(转)180度
z_roll_right_180 && z_roll_left__90 = z_roll_right_90;
z_roll_right_180 && z_roll_right_90 = z_roll_left__90;
z_roll_right_180 && z_roll_right_180 = 1;
z_roll_right_180 && x_mirror = y_mirror
z_roll_right_180 && y_mirror = x_mirror
x_mirror && z_roll_left__90 = 平面以"\"对角线镜像,以向量($y-$x)为轴, 右(手)旋(转)180度
x_mirror && z_roll_right_90 = 平面以"/"对角线镜像,以向量($x-$y)为轴, 右(手)旋(转)180度
x_mirror && z_roll_right_180 = y_mirror
x_mirror && x_mirror = 1
x_mirror && y_mirror = z_roll_right_180
y_mirror && z_roll_left__90 = 平面以"/"对角线镜像,以$x-$y轴, 右(手)旋(转)180度
y_mirror && z_roll_right_90 = 平面以"\"对角线镜像,以$y-$x轴, 右(手)旋(转)180度
y_mirror && z_roll_right_180 = x_mirror
y_mirror && x_mirror = z_roll_right_180
y_mirror && y_mirror = 1
-----------------------------------------------------
"/"_mirror && z_roll_left__90 = x_mirror
"/"_mirror && z_roll_right_90 = y_mirror
"/"_mirror && z_roll_right_180 = "\"_mirror
"/"_mirror && x_mirror = z_roll_left__90
"/"_mirror && y_mirror = z_roll_right_90
"\"_mirror && z_roll_left__90 = y_mirror
"\"_mirror && z_roll_right_90 = y_mirror
"\"_mirror && z_roll_right_180 = "/"_mirror
"\"_mirror && x_mirror = z_roll_right_90
"\"_mirror && y_mirror = z_roll_left__90
-----------------------------------------------------
具体的直观图:
http://blog.csdn.net/tiandyoin/article/details/43764329