Kalman 滤波 跟踪

===================知识来源于网络。汇总整理。========== thx to the author=======================

kalman滤波de基本思想就是先不考虑输入信号和观测噪声的影响，得到状态变量和输出信号的估计值，

再用输出信号的估计误差加权后校正状态变量的估计值，使状态变量估计误差的均方差最小。

OpenCV已经把Kalman滤波封装到一个类KalmanFilter中了。

想要用kalman滤波，要知道前一时刻的状态估计值x，当前的观测值y，还得建立状态方程和量测方程，才可以运用kalman滤波了。

code：[来自opencv2.3.1/samples/cpp/kalman.cpp]

#include"stdafx.h"
#include "opencv2/video/tracking.hpp"
#include "opencv2/highgui/highgui.hpp"

#include <stdio.h>

using namespace cv;

static inline Point calcPoint(Point2f center, double R, double angle)
{
	return center + Point2f((float)cos(angle), (float)-sin(angle))*(float)R;
}

void help()
{
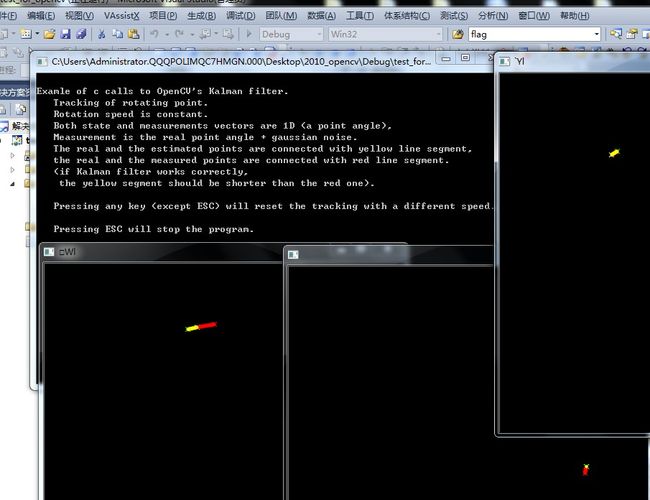
	printf( "\nExamle of c calls to OpenCV's Kalman filter.\n"
		"   Tracking of rotating point.\n"
		"   Rotation speed is constant.\n"
		"   Both state and measurements vectors are 1D (a point angle),\n"
		"   Measurement is the real point angle + gaussian noise.\n"
		"   The real and the estimated points are connected with yellow line segment,\n"
		"   the real and the measured points are connected with red line segment.\n"
		"   (if Kalman filter works correctly,\n"
		"    the yellow segment should be shorter than the red one).\n"
		"\n"
		"   Pressing any key (except ESC) will reset the tracking with a different speed.\n"
		"   Pressing ESC will stop the program.\n"
		);
}

int main(int, char**)
{
	help();
	Mat img(500, 500, CV_8UC3);
	KalmanFilter KF(2, 1, 0); //kalman滤波器---状态维数2，测量维数1，没有控制量
	Mat state(2, 1, CV_32F); //(phi, delta_phi)两个状态 （角度，角速度）
	Mat processNoise(2, 1, CV_32F); 
	Mat measurement = Mat::zeros(1, 1, CV_32F); ////观测量，应该是角度吧
	char code = (char)-1;

	for(;;)
	{
		randn( state, Scalar::all(0), Scalar::all(0.1) );
		KF.transitionMatrix = *(Mat_<float>(2, 2) << 1, 1, 0, 1); //初始化 状态传递矩阵,给矩阵赋初值

		setIdentity(KF.measurementMatrix); //初始化 测量矩阵
		setIdentity(KF.processNoiseCov, Scalar::all(1e-5)); //噪声协方差矩阵
		setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1)); //测量噪声协方差矩阵
		setIdentity(KF.errorCovPost, Scalar::all(1));//先验误差计协方差矩阵

		randn(KF.statePost, Scalar::all(0), Scalar::all(0.1)); //statePost:矫正状态 x(k)=x'(k)+K(k)*(z(k)-H*x'(k))

		for(;;)
		{
			Point2f center(img.cols*0.5f, img.rows*0.5f);
			float R = img.cols/3.f;
			double stateAngle = state.at<float>(0); //初始角度
			Point statePt = calcPoint(center, R, stateAngle); //由角度计算出初始点的坐标

			Mat prediction = KF.predict(); //第一步调用成员函数predict得到 当前状态变量 的估计值
			//predicted state (x'(k)): x'(k)=A*x(k-1)+B*u(k)
			//x(k-1)为前一状态的校正值，第一个循环中在初始化过程中已经给定了，后面的循环中Kalman这个类内部会计算。
			//A,B,u(k),也都是给定了的值。这样进过计算就得到了系统状态的预测值x'(k)了。 
			double predictAngle = prediction.at<float>(0); //使用kalman预测的 角度
			Point predictPt = calcPoint(center, R, predictAngle); //求出预测点的坐标

			randn( measurement, Scalar::all(0), Scalar::all(KF.measurementNoiseCov.at<float>(0))); 

			// generate measurement
			measurement += KF.measurementMatrix*state; //当前观测值measurement = 测量矩阵measurementMatrix * 状态估计值state

			double measAngle = measurement.at<float>(0); //测量角度
			Point measPt = calcPoint(center, R, measAngle); //测量值（坐标）

			// plot points
			// 这个define语句定义了一个画小十字的函数
#define drawCross( center, color, d )                                 \
	line( img, Point( center.x - d, center.y - d ),                \
	Point( center.x + d, center.y + d ), color, 1, CV_AA, 0); \
	line( img, Point( center.x + d, center.y - d ),                \
	Point( center.x - d, center.y + d ), color, 1, CV_AA, 0 )

			img = Scalar::all(0); //Scalar(B, G, R)
		/*
			drawCross( statePt, Scalar(255,255,255), 3 ); //真实位置corrected state，用白色十字叉画出
			drawCross( measPt, Scalar(0,0,255), 12 ); //测量的点，用红色十字叉画出
			drawCross( predictPt, Scalar(0,255,0), 3 ); //预测点，用绿色的小十字叉标出
			line( img, statePt, measPt, Scalar(0,0,255), 13, CV_AA, 0 ); //用红色的线画出真实值到测量点的线段
			line( img, statePt, predictPt, Scalar(0,255,255), 3, CV_AA, 0 ); //用红色的线段画出真实值到估计点的线段
		*/
			circle(img, statePt, 10, CV_RGB( 255, 0, 0), 3, 8, 0); //红色，真实位置
			circle(img, measPt, 10, CV_RGB( 0, 255, 0), 2, 8, 0); //绿色，测量坐标
			circle(img, predictPt, 10, CV_RGB( 0, 0, 255), 2, 8, 0); //蓝色，预测坐标

			KF.correct(measurement); //调用成员函数correct 用 观测值 校正 状态变量
			//corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
			//x'(k)为predicted state, z(k)为当前测量值，是我们外部测量后输入的向量。
			//H为Kalman类初始化给定的测量矩阵。K(k)为Kalman增益

			randn( processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at<float>(0, 0))));
			state = KF.transitionMatrix*state + processNoise;  //状态转移方程为 :状态state = 状态转移矩阵transitionMatrix * 状态 + 噪声
			                                                  //加上噪声之后就不是匀速运动了。。
			imshow( "Kalman", img );
			code = (char)waitKey(100);

			if( code > 0 )
				break;
		}
		if( code == 27 || code == 'q' || code == 'Q' )
			break;
	}

	return 0;
}

ps：

对旋转的点的跟踪。 点旋转的速度是恒定的。 状态和测量矩阵都是一维的(虽然点时再二维平面上运动，但是其角速度是恒定的，所以变化的只有角度一个变量)

测量值measurement 是真实的点的位置 + 高斯噪声 之后的位置。

/*   */ 之内的代码：

黄色线段代表： 真实的点的位置+估计的点

红色线段表示： 真实的点和测量measured 点 

[当 黄色的线段  短于  红色的线段的时候，表示  kalman滤波器预测的是正确的]

===

看着晃眼，就简单画了三个小圈圈。

tutu:

=====

=======================================

          简单来说，卡尔曼滤波器是一个“optimal recursive data processing algorithm（最优化自回归数据处理算法）”。对于解决很大部分的问题，他是最优，效率最高甚至是最有用的。他的广泛应用已经超过30年，包括机器人导航，控制，传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等等。近年来更被应用于计算机图像处理，例如头脸识别，图像分割，图像边缘检测等等。

一篇很形象的文章：

http://www.cnblogs.com/feisky/archive/2009/11/09/1599247.html