杭电OJ（HDOJ）1392题：Surround the Trees（凸包问题）

题意：

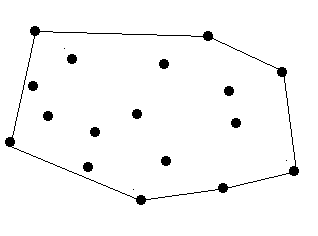
一个土地上有N棵树，农夫想把所有的树用一根绳子绕起来，给出每棵的坐标（X，Y），求出绳子的最短长度。树至少有1棵，至多的100棵，坐标均为整数且不超过 32767。输出的最短长度保留两位小数。先给出树的棵数n，后输入n棵树的坐标，当n为0时，测试结束。（引用原图）

示例输入：

9 

12 7

24 9 

30 5 

41 9 

80 7 

50 87 

22 9 

45 1

50 7

0

示例输出：

243.06

解决方案：

图中四个点确定了三条直线AB，BC，BD。图中所有的点都在AB的下方，AB的上方没有一个点，发现凸包所有的外围边都有和AB边一样的特点，将所有的点分隔到该线段（AB）的一侧，另一侧没有任何点。BD同样具有这样的性质，所以BD也是凸边的外围边。但是BC（蓝色的边）的右边还有一个点D所以BC不是凸包的外围边。可以确定：只要两点所确定的直线可以将平面所有的点都划分到一侧，另一侧没有任何点，这两个点就是外围边上的点。

已知两个点A，B和其坐标，可以求两点所在直线的方程式ax+by-c=0，a=y2-y1，b=x1-x2，c=x1y2-y1x2。将第三个点的坐标x，y代入这个方程所得的等于0，则这个点就在这条直线上，小于0就在直线的一侧，大于0就在直线的另一侧（具体在哪一侧跟具体方程有关）。只要两个点确定一条直线后，将其它（n-2）个点代入直线方程，要么全部>=0,要么全部<=0，就可以确定这两个点为外围边上的点。

任意不相等两个点的组合可以一个双层循环取出相应的组合（共有n(n-1)/2种组合），判断其它（n-2）点都在两点所确定的直线的一侧，又需要一个循环，所以一共需要三重循环，程序的时间复杂度就是O(n^3)。

1、根据题意和图片就知道这是凸包问题；

2、注意树只有1和2棵时也要输出，这题测试有点不太严谨，当有2棵树（A和B）时，绳子的长度应有2*|AB|，但这里却只有|AB|；

3、这个题目的解决是参考《算法设计与分析基础》第三章的蛮力法解决，所以时间复试度为O(n^3)，非常大了。

#include<stdio.h>
#include<math.h>
typedef struct point
{
    int x;
    int y;
} Point;

Point arr[100];//坐标数组
int n;//坐标数组长度
double convexHullLength;//凸包长度

void inputPoint()//坐标输入函数
{
    int i;
    for(i=0; i<n; i++)
        scanf("%d%d",&arr[i].x,&arr[i].y);
}

double Distance(int p1,int p2)//计算两点之间的距离
{
    return sqrt(pow(arr[p1].x-arr[p2].x,2)+pow(arr[p1].y-arr[p2].y,2));
}

int judgePoint(int p1,int p2)//判断两点是(1)否(0)在凸包外围边上
{
    int big,small,i,a,b,c,line;
    a=arr[p2].y-arr[p1].y;
    b=arr[p1].x-arr[p2].x;
    c=arr[p1].x*arr[p2].y-arr[p1].y*arr[p2].x;
    big=small=0;
    for(i=0; i<n; i++)
    {
        line = a*arr[i].x+b*arr[i].y-c;
        if(line>0)
            big=1;
        if(line<0)
            small=1;
        if(big&small) return 0;
    }
    return 1;
}
int main()
{
    int i,j;
    while(scanf("%d",&n)&&n)
    {
        convexHullLength=0;
        inputPoint();
        if(n==1)
            printf("0\n");
        else if (n==2)
            printf("%.2lf\n",Distance(0,1));
        else
        {
            for(i=0; i<n; i++)
                for(j=i+1; j<n; j++)
                {

                    if(judgePoint(i,j)==1)
                    {
                        convexHullLength+=Distance(i,j);
                    }

                }
            printf("%.2lf\n",convexHullLength);
        }

    }
}