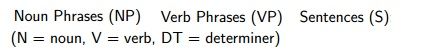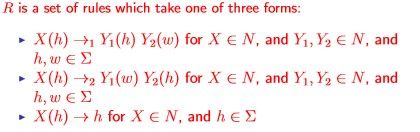NLP 学习笔记 03 (Probabilistic Context-Free Grammars (PCFGs))
最近一周有些拖沓,静下来把第3,4周的笔记写了
这两周的主题都是PCFGs,不过从浅到深,逐层深化罢了,所以题目就用Probabilistic Context-Free Grammars (PCFGs)了
1.Introduction
----------------------------------------------------------------------------------
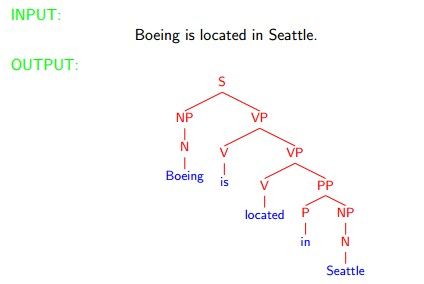
语法树:这在编译原理课上就学过了,也就是用树的形式来表示语法,例如:
-------------------------------------------------------------------------------
上下文无关语法 (Context-Free Grammars) :
一个上下文无关语法是一个四元组2:
其中N是一组非终结符(non-terminal symbols)
Σ是一组终结符(terminal symbols)
R是一系列的变换规则,即是:
S是一个特殊的开始符号
-------------------------------------------------------------------------------
2.Ambiguity
接下来课程用了相当一段时间介绍了一个极简单的英语语法模型,这里也不再无意义地详细描述了
然后提到了一下模糊化的问题,这也很好理解,因为在编译原理课上也有比较详细的解释
也就是一个句子可能有不同的语法书对其进行解释,比如:
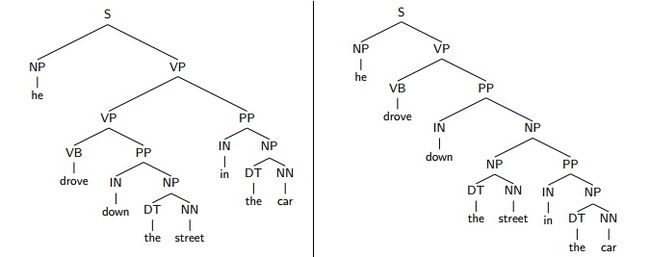
或者一个词汇有不同的词性,这也会影响到描述它的语法树,如:duck既可以作名词,也可以做动词
第一种情况的解决方法就是用最左推导,也就是尽量先展开推到规则中最左边的非终结符,当然这也不是很好的方法,可以参考使用pcfgs
第二种情况就要用到下面的pcfgs了
3.Probabilistic Context-Free Grammars
现在切入到正题了,PCFGs其实就是在
Context-Free Grammars的基础上对每个RULE,也就是R中的内容加以概率限制
这样我们就可以根据这样一个表求出一个句子用特定语法树的概率值,具体来说就是将该语法树所有使用的规则的概率乘起来
加入我们有一系列的语法树都可以扩展出一个句子,将这些语法记作
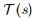
然后我们可以对每个语法树求概率,并选取概率最大的一项作为我们的返回树:
4.Chomsky Normal Form && A Dynamic Programming Algorithm
Chomsky Normal Form的PCFG和上面介绍所定义的pcfg区别就在于每个非终结符只能推导出两个非终结符或者一个终结符
要把一个普通的PCFG变成一个Chomsky格式的也很简单,对于每个有两个以上的rule:
在此基础上有一个动态规划的算法来求出最好的语法树:
-------------------------------------------------------------------------------------------------------------------------------
下面是定义,我就懒得翻译了~~~
一句话 π(i,jX)表示句子中从i到j之间用非终结符X推导出来的最大概率~~~~~
最开始的值当然简单:这是很自然的事
递推式:
也就是枚举一下分隔符,将i-j的句子分成两部分,看那一条X的推到规则能够取得最大的概率
5.Lexicalized PCFGs
PCFGs的精确度只能达到72%,而现代的方法能达到92%,它的一个明显的缺点就是对词汇不敏感,什么意思呢?
对于这个树,pcfgs对于IBM这个词的概率判断与整个树的其它地方都没有任何关系。
又比如:
上面两颗不同的树表示了同一个句子,右边是他们所使用的规则,仔细发现它们只有黑体字的两条是不同的,也就是说这两棵树的概率大小只取决于这两个规则的概率,与这个句子的词没有关系了~~~这明显是一个很不好的地方,所以教程后面接着讲了
Lexicalized PCFGs。
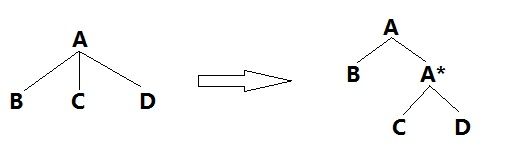
Lexicalized PCFGs首先定义了每条规则的‘head’,也就是该条规则的主体是什么,如下图的左图,红色为‘head’
然后将整棵书表示为右图的形式,括号内的内容是当前节点的head所最终指向的单词,这是一个逐层上传的过程,比如:Vt的head是questioned,而VP的主题是Vt,也就是questioned,而S的head是VP,也就是questioned。
针对这个特性,将PCFGs四元组中的R规则修改为:
这个模型的朴素计算复杂度高达
 ,但实际上通过一些剪枝,比如如果一个词w没有出现在句子里,所有终结符X都不会有对应的X(w)出现,最终可以将计算复杂度减少到
,但实际上通过一些剪枝,比如如果一个词w没有出现在句子里,所有终结符X都不会有对应的X(w)出现,最终可以将计算复杂度减少到
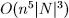 。
。
6.A Model from Charniak (1997)
这是一个97年的模型,可以想象我们学的还是多么“古老的”东西,不管怎么说从基础开始吧
如何来计算这些rule的概率呢,一个Charniak的模型就是:
首先将一个rule分解成两部分
然后对右边两个乘数使用smooth,计算
qML计算就和之前讲的一样啦,用整个式子的统计和除以条件项的统计和
7.Dependency Accuracies
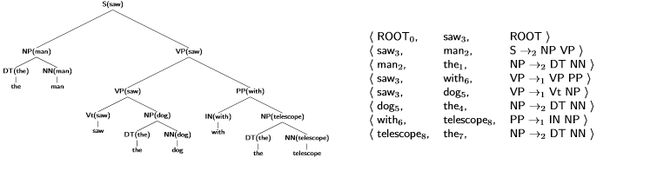
来衡量一颗树的精度Accuracy,(意思是与标准的答案作对比),首先介绍一种树的表示方式
每个单词下面的下标数字是这个词在句子中的序号,而右边每一行表示了一个节点所使用的规则和该规则下面的head值,比如第二行就是根节点的表示,除此之外加入了一个特殊的表示,就是第一行。
然后根据如下规则计算出该表示的recall和accuracy:
其中的斜杠是‘或者’的意思~~不是除法,这个理解起来也不是很难,所谓的dependencied就是上上图右边的那些项目,这个模型大概有88%的精度