第九周项目2-(2)对称矩阵的加法和乘法
问题及代码:
/*
void Init(int *&b);//为N阶对称矩阵初始化存储数据的一维数组b
int Value(int b[], int i, int j);//返回存储在b[M]中,对应二维数组A[i][j]的值
void Assign(int b[], int e, int i, int j);//将e赋值给对应二维数组元素A[i][j],要存储到b[M]中
void Disp(int b[]);//输出压缩存储在b中的对称矩阵
void Destroy(int b[]); //销毁存储空间
并实现:
设计算法,实现两个用压缩形式存储的对称矩阵A和B的加法和乘法。实现中请使用好前面设计的基本运算
*/
#include <stdio.h>
#define N 4
#define M 10
int value(int a[],int i,int j)
{
if (i>=j)
return a[(i*(i+1))/2+j];
else
return a[(j*(j+1))/2+i];
}
void madd(int a[],int b[],int c[][N])
{
int i,j;
for (i=0; i<N; i++)
for (j=0; j<N; j++)
c[i][j]=value(a,i,j)+value(b,i,j);
}
void mult(int a[],int b[],int c[][N])
{
int i,j,k,s;
for (i=0; i<N; i++)
for (j=0; j<N; j++)
{
s=0;
for (k=0; k<N; k++)
s=s+value(a,i,k)*value(b,k,j);
c[i][j]=s;
}
}
void disp1(int a[])
{
int i,j;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
printf("%4d",value(a,i,j));
printf("\n");
}
}
void disp2(int c[][N])
{
int i,j;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
printf("%4d",c[i][j]);
printf("\n");
}
}
int main()
{
int a[M]= {1,2,3,4,5,6,7,8,9,10}; //a表示压缩存储的对称矩阵
int b[M]= {1,1,1,1,1,1,1,1,1,1};
int c1[N][N],c2[N][N];
madd(a,b,c1);
mult(a,b,c2);
printf("a矩阵:\n");
disp1(a);
printf("b矩阵:\n");
disp1(b);
printf("a+b:\n");
disp2(c1);
printf("a×b:\n");
disp2(c2);
printf("\n");
return 0;
}
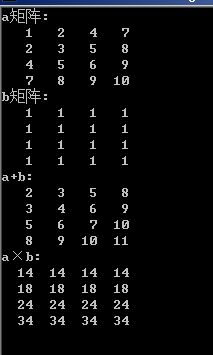
运行结果:
知识点总结:
与对称矩阵的知识点相同,增加的内容为矩阵的加法和乘法运算,实现方法为套用回赋值函数中,乘法的实现需要运用 s=s+value(a,i,k)*value(b,k,j);
心得体会:
算法中比较难得部分可以运用分部调试+画图的方法进行理解和总结。