Mining Massive Datasets课程笔记（一）

MapReduce and PageRank

一、Distributed File System （分布式文件系统）

why do we need mapreduce？
传统的数据挖掘方式（single node architecture)在处理海量数据（Like 200TB）时，由于CPU和disk之间的bandwidth限制以及单个CPU的处理能力限制，使得数据处理的时间成本非常高，从而有了多个节点多个CPU并行处理的想法。因此提出了cluster architecture。

在cluster Architecture中每个机架（rack）有16-64个节点，他们由千兆交换机相连，这些机架之间再由骨干交换机继续联系。这种结构曾经被广泛运用在大型数据集的存储和处理中，但是它并没有完全解决问题，仍有自己的局限性：
1、node failures

节点作为物理实体很可能会在运行中失效，那么在节点可能失效的情况下：
如何能稳定有效地提供数据存储？
在长时间的计算过程中如果遇到节点失效该如何处理？*（重新计算无疑很浪费时间很低效）*

2、network bottleneck

即使网络带宽是1Gbps，移动10TB的数据也要将近1天的时间。而稍微复杂些的计算都可能需要多次数据移动的过程，因此会使得计算速度很慢。因此需要找到一种新的方法在计算过程中减少数据的移动。

3、Distributed Programming is hard
Need a simple model that hides most of the complexity

MapReduce的出现解决cluster Architecture存在的三个问题
问题1：MapReduce通过将数据冗余存储在多个节点上从而解决节点失效的问题。
问题2：MapReduce通过move computation close to data 来减少数据用移动从而最大限度减小网络带宽的限制问题
问题3：MapReduce通过提供一种simple programming model来隐藏分布式架构的复杂性

下面具体讲解这三个解决方案的实现方式：
1、Redundant Storage Infrastructure——Distributed File System
分布式存储系统提供冗余存储，提供全局的文件命名空间、具有冗余性和可用性。典型的例子有谷歌的GFS以及Hadoop 的HDFS。典型的应用模式是Huge files: 数据通常写入一次但读取多次，并经常添加新数据但是很少更新或更改已有数据。

Distributed File System：
数据或文件通常被分割并存储在不同机器的chunks中，因此也叫这些存储数据的机器为chunk server。被一个chunk都被复制和保存在不同的机器上从而实现冗余存储。chunk server同时也扮演这compute server的角色，计算到那个chunk的数据时就使用存储该chunk的机器作为compute server从而实现move computation close to data避免了数据的移动 。

因此分布式文件系统主要包含下面三个部分：

二、The MapReduce Computational Model

work count 例子：计算在一个Huge text document 中某个词出现的次数，引申应用还有计算网页服务器日志中最受欢迎的网页链接以及研究中的术语统计等等问题。
在unix中可以使用下列命令直接实现：

这句命令实际上就体现了mapReduce的实现过程，但MapReduce厉害在很自然地实现了各部分的并行化。

MapReduce的总体框架都是一样的，不同的问题对应的只是Map和Reduce function的变化。
具体来说，

MapReduce基于顺序读取的硬盘

三、Scheduling and Data Flow

这部分将具体讲解MapReduce的运行机制
如下图左边是单个机器上的MapReduce过程。首先对一个大的文本（输入的数据）进行读入和分块，在各个chunk中使用Map函数形成键值对（key-value)；然后进行Group操作，通常用于Reduce操作的节点比Map的要少，所以需要group操作来将Map函数得到的相同的key映射到对应的Reduce函数中，通常用到的group方法有Hash merge，shuffle，sort以及partition等。最后由Reduce函数sort出相同的key放在一起，并计算和输出最终结果。
右图是在分布式系统上的MapReduce。

因此，Programmer只需要提供明确的输入文件，以及Map函数和Reduce函数，而MapReduce environment 需要提供其余事情的处理：

• 对输入的数据进行分块
• 调度程序在多台机器上运行（多个机器上的Map函数并行等）
• 上文提到的Group by Key操作
• 处理节点失效的情况
• 处理机器间的通信问题
• 。。。

Data Flow

输入和输出数据保存在分布式文件系统（DFS）：DFS在上文第一节中已经讲过，调度机会尽量将Map tasks安排在离存储有该Map函数输入数据的机器上（因为chunk server同时也是compute server）

中间结果将存储在本地（map and reduce workers)的文件系统中

一个Map-Reduce task的输出往往是另一个Map-Reduce task的输入

Coordination: Master

master node负责任务调度：
任务的状态有三种（idle，in-progress，completed）；当有可用的workers时idle tasks立即被调度；当一个map task结束时它会向master节点发送R个中间结果的位置和大小信息，每一个对应一个reducer；master节点将这些信息发送给reducers.

master 节点会周期性的ping workers以确保节点没有失效。

Dealing with Failures

Map worker failure：如果map tasks完成了或者正在进行（completed or in-progress），task将会被设置为idle。因为idle tasks最终会被重新分配到其它工作节点上运行

Reduce worker failure：只有in-progress task会被设置为idle并重新调度在别的worker执行。
因为Reduce的输出就是final output，它已经被写入到DFS中，而map的输出是中间结果在local DFS中，所以Reduce worker中的completed task没必要重新调度执行。

Master failure：MapReduce task终止并且发出警告，Master node没有复制
当然它作为单个节点fail的概率也很低。

How many Map and Reduce jobs?

M要比集群中的node数量大很多，通常给每一个DFS chunk分配一个Map，这样提高了动态负载平衡以及加速了worker failures的恢复。
R一般比M要小，因为最终的输出是需要将R个输出文件集中起来的，所以少的数量会比较好。

四、Combiners and Partion Functions

第三节详细介绍了基础的MapReduce，这一节主要介绍两种refinements来完善MapReduce。

Refinement : combiners

首先我们思考这样一种状况：在前面的word count例子中，一篇文章中通常都会有高频词汇，例如 “The”在许多文章的出现次数都非常高，如果按照basic MapReduce来操作，将会产生非常相同的key，都需要发送到同一个Reducer，将会因为这一个的传输浪费大量网络带宽。
处理方式就是在每一个Mapper中添加combiner，pre-aggregating values in the mapper。在word count中即提前计算相同key出现的次数。
通常combiner函数都和reduce函数相同。

不难想象，combiner trick只有在reduce函数满足交换律和结合律时才适用，如sum求和函数。当然也可以将不满足交换律和结合律的函数进行相应的变换，如avg求平均函数，我们可以每次都计算相同key的sum以及总的计数count，最后在reduce中再进行sum/count计算。
还有一些操作不管怎样都无法使用Combiner，例如Median求中位数。

Refinement : Partition Function

Map操作结束后默认是使用hash（key)mod R 来将相同的key分配到相同的Reduce worker，partition function可以提供新的分配函数，来让用户决定如何将map函数的key, value pairs go to which Reduce worker。
例如使用hash（hostname(UrL)) mod R来确保来自同一个host的URLs被被分配到同一个reduce中去

五、Link Analysis and PageRank

从本节开始讲一个新的topic： Graph Data

首先探讨Link Analysis方法，例如PageRank或者SimRank；然后也会探讨Community Detection，希望找出网络中节点的集群；以及spam Detection，希望能鉴别Spam nodes in the graph。

首先，我们将网络web看成一个巨大的有向图，其中webpages就是图的节点，网页间的超链接links看做是边。从而提出如何organize the web的问题。早期是通过人工分类，后来又尝试使用web search将相似的网页聚类到一起，但是网络本身是非常huge的，且有很多不可信的内容以及不相干的信息等。因此，web search 面临两大问题：

要解决这些问题，首先要将web看做是一个大的图，并且计算图中各个节点的重要性，当然不同网页的重要性是不同的，首先我们rank the pages by the link structure.我们先简单地根据link越多的节点，分数就越高来计算。
计算节点重要性的方法有：

六、PageRank： The Flow Formulation

首先介绍第一种计算节点重要性的方法——PageRank。首先探讨下PageRank的数学式，首先用最基础和直观的式子来表达，我们称之为The Flow formulation，然后进一步地给出数学上的推导，具体地探讨它是如何计算重要性分数的。最后再根据结果修正起初的算式。
因此，首先我们简单地认为links as votes.

• links越多重要性越大；
• 这里的links是in-links而不是out-links. 因为in-links比out-links更难以伪造（or sometime like that…）；
• 同时，我们也不难理解不同的in-links应该具有不同的重要性，比如来自斯坦福大学官网的inlinks就比从我的博客的过去的inlinks要高大上很多(⊙ o ⊙ )
• 对于一个page的所有out-link来说，它们平分这个page的importance score

因此，我们就有了下列这个recursive formulation：

如下图所示，会出现循环定义的问题，因此需要一个限定式才行。

对于上述式子使用高斯消元法就能求解，但是对于大的网络图就不行了。因此需要new formulation~

七、PageRank：The Matrix Formulation

为了更好地解决大规模网络图的问题，使用矩阵来重新定义PageRank，从而可以用线性代数来求解。

首先定义一个随机邻接矩阵M：邻接矩阵是通常用来表达图中节点与节点的邻接关系的矩阵，而随机矩阵，又称为马尔科夫矩阵是用来描述一个马尔可夫链的转变的矩阵，它的每一项都是一个表示概率的非负实数。
右随机矩阵（行随机矩阵）：实方阵，其中每一行求和为1
左随机矩阵（列随机矩阵）：实方阵，其中每一列求和为1
假设网页i 有di个out-links，则每个从网页i 进入的页面在矩阵M中记作1/di，否则记作0。因此矩阵M是一个列随机矩阵。
同时，定义了向量r :表示每个页面的重要度（和为1），计算方法上一节说过。
最后如何得到r = M * r 这个矩阵式，以及它的意义是什么？
根据下图这个例子，矩阵M的第i列表示从节点i出发到各个节点是否有边（有则为di，无则为0），因此第j行表示节点j的所有in-links。因此第j行和向量r的内积即为节点j的重要度rj。

有了这个式子后对我们求解r向量有什么用呢（因为我们要求解每个节点的重要度）

首先我们回忆下特征向量和特征值的概念，特征值方程：Av=λv
如果向量v与矩阵A满足 Av=λv（λ为一个常量）则称向量v是变换A的一个特征向量，λ是相应的特征值。
有关特征值与特征向量的内容在另一篇博客中详细讲：
因此上面那个式子可以看做是λ=1时对矩阵M求特征向量r，因此我们就可以高效地求得节点的重要度了，下面介绍求解这个特征向量r的方法，我们称之为 Power Iteration

八、PageRank：Power Iteration

还是以web graph 为例，假设有n个节点（页面），页面间的超链接为节点间的边。首先给各个节点一个初始的重要度1/N，由r=M*r这个式子经过50~100次迭代后直到收敛，将此时的r向量作为近似解。当然这里收敛的判别式可以是L1范式也可以是欧几里得范式，只要能判断收敛即可。

具体的例子就不写了比较好理解，那么这里通过PageRank得到的分数的意思是什么呢，下面使用随机游走来解释：
想象一个网络上的随机游走者（surfer），在任意时间t处于网页i，在下一时间t+1，surfer会从i的out-links中随机挑选一个达到网页j。

因此我们可以定义一个向量p(t)，向量中的第i个元素表示在t时刻surfer处于页面i的概率。因此p(t)表示页面的概率分布。

so where is the random walker going to be at time t+1?
下面我们考虑surfer在t+1时刻处于节点j的概率。因此我们需要考虑所以指向节点j的这些i1,i2,i3,…节点，因此和之前的PageRank是相同的。

可以想象surfer游走到某一时刻时如果p(t+1) = p(t)，则说明达到了这个网络图的稳定分布，而之前的向量r就满足这个稳定分布。
因此，page rank score代表着random surfer随机游走中在给定的时刻t时位于特定节点的概率分布。

existence and Uniqueness

随机游走又称为马尔科夫过程，对于满足特定条件的图，不论初始的概率分布是怎样的，最终都能达到一个唯一的稳定分布状态。
后面的章节会探讨这个特定条件是什么样的

九、PageRank： The Google Formulation

上一节说到满足特定条件的图有唯一的稳定分布，那么针对前面PageRank的Flow formulation以及matrix formulation就有了下面三个问题存在：

根据这三个我们问题，我们来探讨下Google formulation是如何实现PageRank的。
1. 是否收敛：“Spider trap”问题

像这种所有out-links都在一个组内就会造成spider trap问题
解决方式：random teleports

1. 是否收敛到想要的程度：“Dead End”问题
   
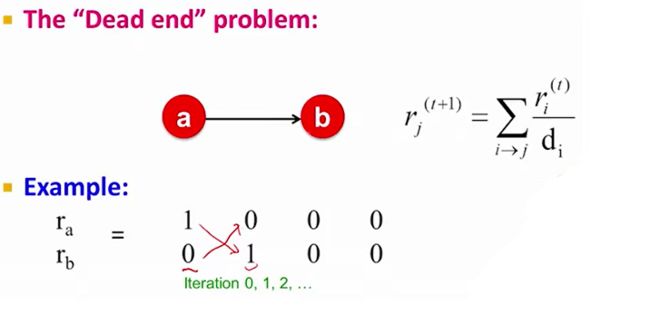
   在实际的网络中，通常有很多页面是没有out-links的，就会造成dead end 问题，如果以随机游走的解释来看就很好理解了，surfer到这里后就没有out-links可以走了，那么下一时刻去其它节点的概率最终都会变为0
   解决方式：Always teleports
   

2. 收敛结果是否合理： 以上两种都是不合理的

十、Why Teleports Solve the Problem

这一节主要讲的是为什么通过teleports可以解决上述问题，首先我们先讲解下马尔科夫链Markov chains. P(i,j)表示从节点j到节点i概率。

马尔科夫链的理论指出，对于任意的开始向量，对马尔科夫变换P使用power method都将会收敛到一个唯一的正稳态向量：它的充要条件是矩阵P是stochastic（满足随机矩阵），irreducible的以及aperiodic非周期性的。

接下来我们就会看到上一节提到的teleports方法就可以使得矩阵P拥有上述三个性质，从而保证了稳定分布的存在性和唯一性。

Make M Stochastic

满足stochastic的矩阵说明每一列的和为1，对于dead end 节点来说列的和为0，因此需要添加绿色的links，如下图：

图PPT中的式子有错，应该改成下面这样：
A=M+1neT⋅a

Make M Aperiodic

如下图所示的循环链中，random teleports加入绿色链接，从而保证了每两次访问某个节点的时间间隔是非周期性的。

Make M Irreducible

对于任意的状态，从任一状态转换到另外任一状态的概率不能为0。

Google formulation同时解决了上述三个问题：

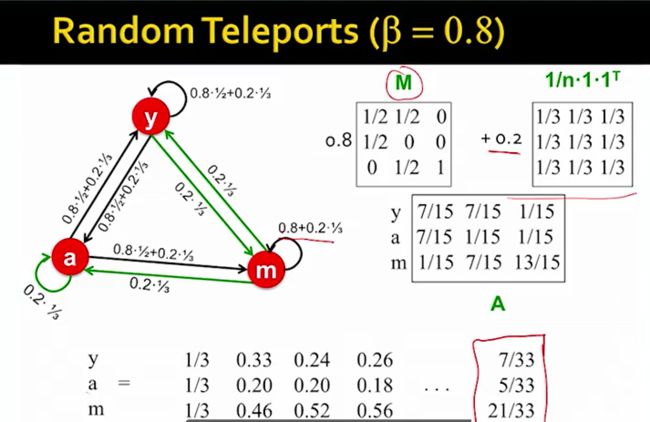
当 β=0 时相当于surfer一直随机挑选节点，则所有节点的PageRank score都将是一样的；当 β=1 时相当于还是和前几节的基础表达式一样，当出现dead end等问题时就会出错，因此通常将 β 值设为0.8到0.9之间，如0.85。
下面用一个实际的例子说明PageRank score的计算过程：

十一、How we Really Compute PageRank

通过上面的学习，计算Page Rank的方法已经有了，当内存足以容纳A， r(old) r(new)时很容易，那么对于大规模的网络通常内存存不下，那么该怎么办呢？
我们可以想象在成千成万的网页形成的邻接矩阵M（稀疏矩阵）中，节点间有边的所占的比例比较小，因此如果我们只保存这些non-zero elements就可以节省大量的存储空间。而前面我们的random teleports使得A矩阵中没有0元素，因此通过下面两张图中的解释和转换得到新的式子：


因此计算过程中我们不再需要存储那个很大的A矩阵，而是可以处理稀疏矩阵M。

总之，PageRank的完整算法如下图：

Ref：
https://class.coursera.org/mmds-003/lecture
http://blog.csdn.net/xyd0512/article/details/43848631
http://blog.csdn.net/sherrylml