[置顶] 算法复杂度精讲——算法时间复杂度的数学原理:从O(n(log(n))说起
概述:在设计算法的时候,要考虑两个方面,一个是算法的正确性,另外一个就是算法的效率,也就是复杂度,通常情况下,我们优先考虑的是时间复杂度,这也是本文要讨论的内容。算法学习的时候,经常碰到这样的问题,为什么快速排序的时间复杂度是O(nlog(n))?为何插入排序的时间复杂度是O(n^2)?这些是我们熟悉的算法时间复杂度,可能病没有太大的问题,那我们不熟悉的呢?如果我们采用三路归并排序而不是二路归并排序,时间复杂度是多少呢?一个排序算法经过某种变形以后时间复杂度又是多少呢?本文,主要从数学底层,讲述一个算法时间复杂度是如何推导的。让你真正知其所以然,而不仅仅是总是心中存有疑惑:为何快排的时间复杂度会是这么奇怪的O(nlog(n))
1.数学基础知识
首先,介绍以下数学基础知识,这些基本都分布在高等数学和离散数学之中,不进行数学推导。
一些不等式:
无论是归并还是快速排序,我们都可以把它们归结到递归/分治这一类问题的求解,他们具有一个一般性的时间复杂度表述:
这个等式的意义是:规模是n的问题可以拆分成a个规模是n/b的问题,那么它的时间复杂度就等于a个规模是n/b的问题,加上一次分解耗费的时间D(n)和一次合并耗费的时间C(n)。第二部分到第四部分将介绍三种求解这个方程式的方法。
2.递归树方法
这是一种最直观的方法,它把上述等式形象化,然后进行求解,我们通过一个例子来说明这个情况。
例子:利用递归树求解T(n)=T(n/10)+T(9n/10)+cn
划出递归树如下:
关键点:求出树的深度和每层的代价(注意,此例中因为每层的代价都相同,所以比较好求解;但在其他情况下,可能是每层代价不同,而是一个等比数列或者其他形式的数列)
1)其中,树的深度容易求解:n-->9/10n-->81/100(n)......n/n=1
也就是说,这个递归下降满足这个趋势(其中b=10/9):
于是
所以
![]()
2)第i层的代价:
每层的规模分别是1/10n和9/10n,而每个节点的代价是cn/10和9cn/10,所以加在一块是cn。
3)总代价:
所以
T(n)=O(nlgn)
3.主方法
形如下列表达式的算法复杂度表述
主方法的证明:参考算法导论第四章
最终利用等比数列的求和公式即可求解。
4.替换代换法
说明:此种方法需要凭借一定的经验,有点类似于数学归纳法,先猜测后证明。
1)步骤:猜测时间复杂度的表述形似
2)要点:猜测要准确,归纳假设要足够强,避免弱化证明。替换非多项式变量
对于边界问题:可采用移动边界和强化归纳假设的方式加以解决。
实例:
1)证明T(n)=T(n/2)+n的时间复杂度位O(nlogn)
令T(n)<cnlgn
说明:此种算法复杂度的计算对以分支法为基础的算法比较有效。
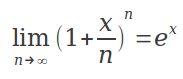
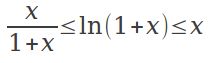
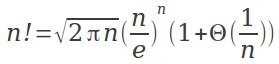

![[置顶] 算法复杂度精讲——算法时间复杂度的数学原理:从O(n(log(n))说起_第1张图片](http://img.e-com-net.com/image/info5/4ae12e28ce7b4151bf33a13b82bf2905.png)
![[置顶] 算法复杂度精讲——算法时间复杂度的数学原理:从O(n(log(n))说起_第2张图片](http://img.e-com-net.com/image/info5/b0499b76f0ef4bc5a77d1d4405f23fe2.jpg)
![[置顶] 算法复杂度精讲——算法时间复杂度的数学原理:从O(n(log(n))说起_第3张图片](http://img.e-com-net.com/image/info5/54ce2a209489491cb3ce1aa22b8dc988.jpg)