uva10233
题意描述:
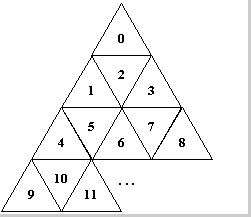
图中都是边长1千米的的等边三角形。每个数字都是在这个等边三角形的外心上,求给出两个数字间的最短距离。(直接连线的长度,最短)
算法描述:
从图中可以看出每行数字个数分别为1,3,5,7,9.。。。。然后我们就从等差数列求和公式得到求和公式f(n) = n^2.所以我们可以求出任意一个数字所在的行,和在这一行中的第几个数。也就是代码中的GetPos()函数。
有了这些信息,我们在看看每行的三角形,有头向上的有头向下的,可以发现,每行的列是奇数的就是向上的,偶数向下,因为外心不是三角的中心,所以要根据三角形的朝向来计算。
有了这些信息,我们就可以连接两点,构造一个直角三角形,计算两点之间的距离。
具体见代码。注意要用long long 啊。因为这里我计算位置的时候n++,如果最大的数+1就超过范围了。
代码:
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstdlib>
using namespace std;
typedef struct Pos
{
long long row;
long long col;
}POS;
POS GetPos(long long n)
{
n ++;
POS pos;
long long k = (long long)sqrt((double)n);
if (k * k == n)
{
pos.row = k;
pos.col = 2 * k - 1;
}
else if (k * k < n)
{
pos.row = k + 1;
pos.col = n - k * k;
}
return pos;
}
long long Swap(long long *n, long long *m)
{
long long p;
if (*n > *m)
{
p = *n;
*n = *m;
*m = p;
}
return 1;
}
int main()
{
long long n,m;
POS posn,posm;
while (scanf("%lld %lld", &n, &m) != EOF)
{
if (n == m)
{
printf("0.000\n");
continue;
}
Swap(&n, &m);
posn = GetPos(n);
posm = GetPos(m);
if (posn.row == posm.row)
{
if (posm.col - posn.col == 1)
{
printf("0.577\n");
}
else
{
double tmp = (posm.col - posn.col)/2.0;
if ((posn.col % 2) ^ (posm.col % 2))
{
printf("%.3f\n",sqrt(tmp * tmp + 1.0 / 12.0));
}
else
printf("%.3f\n",tmp);
}
}
else
{
long long col;
long long row = posm.row - posn.row;
col = posn.col + row;
//prlong longf("%d\n", col);
double x, y, delta, delta1;
x = fabs((double)(posm.col - col)) / 2.0;
if (posn.col % 2)
delta = sqrt(3.0) / 6.0;
else
delta = sqrt(3.0) / 3.0;
if(posm.col % 2)
delta1 = sqrt(3.0) / 3.0;
else
delta1 = sqrt(3.0) / 6.0;
y = delta + delta1 + (row - 1) * sqrt(3.0) / 2.0;
printf("%.3f\n", sqrt(x * x + y * y));
}
}
return 0;
}