ACM-计算几何之凸多边形——hrbust1429

凸多边形

题目：http://acm.hrbust.edu.cn/index.php?m=ProblemSet&a=showProblem&problem_id=1429

Description

已知一个凸多边形A（包含n个点，点按照顺时针给出），和一个点集B（包含m个点），请判断这m个点是否都严格在凸多边形A内部。

Input
输入包含多组测试数据。
对于每组测试数据：
第1行，包含一个整数n (3 ≤ n ≤ 105)代表着凸多边形A的点的数量。
接下来n行每行包含一个坐标(x, y) (-109 ≤ x, y ≤ 109) 表示这个凸多边形，点按照顺时针给出。
第n + 2行，包含一个整数m (3 ≤ m ≤ 105)代表着点集B的点的数量。
接下来m行每行包含一个坐标(x, y) (-109 ≤ x, y ≤ 109) 表示这个点集B。
处理到文件结束

Output
对于每组测试数据：
第1行，如果点集B都严格在凸多边形A内，输出YES，否则输出NO。

Sample Input
4
-10 -10
-10 10
10 10
10 -10
3
0 0
1 1
2 2
4
-10 -10
-10 10
10 10
10 -10
3
100 100
1 1
2 2

Sample Output
YES

NO

计算几何之判断点是否在多边形内，

判断点是否在多边形内有多种方法：射线法，角度和判断法，改进弧长法还有这次用到的二分法。

前三者的时间复杂度均为O(n)，此方法复杂度仅为O（logn）。

而且对于判断很多点是否在多边形内，就可以用这种方法了，耗时少。

原理：

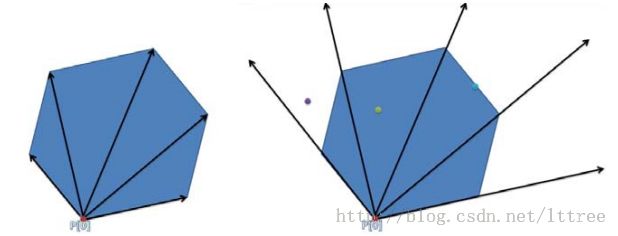
将一个多边形，以其中一个点为原点，开始与其他各点相连并延长做射线，则会形成许多个三角形区域。（如左图）

这样我们可以先判断点在哪两条向量之间。用二分查找，可以很快搜索到。

当然，首先要判断点是否在最左边向量左侧或者最右边向量右侧，如是，则点不在多边形内。

以右图为例，我们找到紫色点在左数第一个三角形区域内，绿色点在左数第二个三角形区域内。

然后，再判断下图所示线段与 所判断点的位置关系。

绿色的线段可以判断绿色的点，左边紫色的点也由相应的线段来判断位置关系。

这样可以判断点是否在多边形内啦。

总结一下：

①建立一个个三角形区域，用其中两条边判断点所在大体区域。

②用第三条边来判断点是否在多边形内。

二分查找就是用在了第一条的地方，用来查找大体区域位置。

明白了这个，就可以做相应的题目来练习一下了！

就是这道题~。~

#include <stdio.h>
struct point
{
    double x,y;
}a[100005],b[100005];
double cross(point p0,point p1,point p2)
{
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}

int main()
{
    int n,m,i,low,high,mid,flag;
    while( scanf("%d",&n)!=EOF )
    {
        for( i=0 ; i<n ; ++i )
            scanf("%lf%lf",&a[i].x,&a[i].y);
        scanf("%d",&m);
        for( i=0 ; i<m ; ++i )
            scanf("%lf%lf",&b[i].x,&b[i].y);
        flag=0;
        for( i=0 ; i<m ; ++i )
        {
            // ① 判断初始时，点是否在凸多边形两最外侧边外面
            if( cross(a[0],a[1],b[i])>=0 || cross(a[0],a[n-1],b[i])<=0 )
            {
                flag=1;
                break;
            }

            // ② 判断凸多边形在哪个三角形里头
            low=2;high=n-1;
            while( low<high )
            {
                mid=(low+high)>>1;      // 就是除以2，比除以2快(位运算比乘除快很多）
                if( cross(a[0],a[mid],b[i])>0 )
                    high=mid;
                else
                    low=mid+1;
            }
            // 查看b是否在凸多边形上面那些边的外面
            if( cross(a[low],a[low-1],b[i])<=0 )
            {
                flag=1;
                break;
            }
        }
        if(flag)    printf("NO\n");
        else    printf("YES\n");
    }
    return 0;
}