GCO3.0的图割分割算法应用(三)

• 该部分对图割算法工具箱（GCO3.0）具体怎么实现简单图像的分割做一个实例。

• 相关理论介绍以及工具箱的介绍见先前博客：

  — 图像分割之图割工具箱GCO3.0的使用（二）
  — matlab实现图割算法中的最大流最小割Max-flow/min-cut问题（一）

一）准备之前

对于一副图像分割之前，需要确定分割成几类，这里以灰度图像为例（彩色图像略复杂），通常来说分割成几类只有两种情况：事先知道该分成几类或者实现不知道该分成几类（这就是自适应分割了）。该工具箱应该是对于事先知不知道几类的都可以处理，对于自适应分割只要找到对应的分割准则即可。为了简单起见，这里以知道类别数来进行实验。
选择经典的lena图像，并将其分割成5类。回顾下图割理论，关于图割中图的构造主要包括两个部分的边权值：点与类中心之间的权值、点与点之间的权值。对于这两部分都以简单的图像灰度信息来构造，点与类中心之间的权值按照点的灰度值与类中心的灰度值差值的平方来计算。点与点之间的权值也可以直接按照灰度相差来计算的，这里以文献上常用的方法来计算。

二）点与类中心权值-datacost

要计算点与类中心的权值大小，点的灰度知道（原始图像就是），那么需要知道类中心的权值，因此需要对图像进行初始化预分类得到开始的一个分类标签，从而得到初始的类中心。这以kmeans来进行预分类如下：

%k-means预分类找到中心与分类
%init_lable预分类，列向量； ctrs-类中心灰度值值
[init_lable,ctrs] = kmeans(img(:),Numlables); %img(:)通过索引转化为列向量可用

其中Numlables是定义的分类数（5），matlab自带的kmeans方法理论上适用于一维情况，而图像是二维的，因此需要把图像转化以一条长链（一维）才能用，得到的ctrs就是开始的类中心（灰度）。然后需要计算的就是所有点中，每个点相对于每个类中心的边权值。把上节画的图再用一遍，形象的相关权值定义如下：

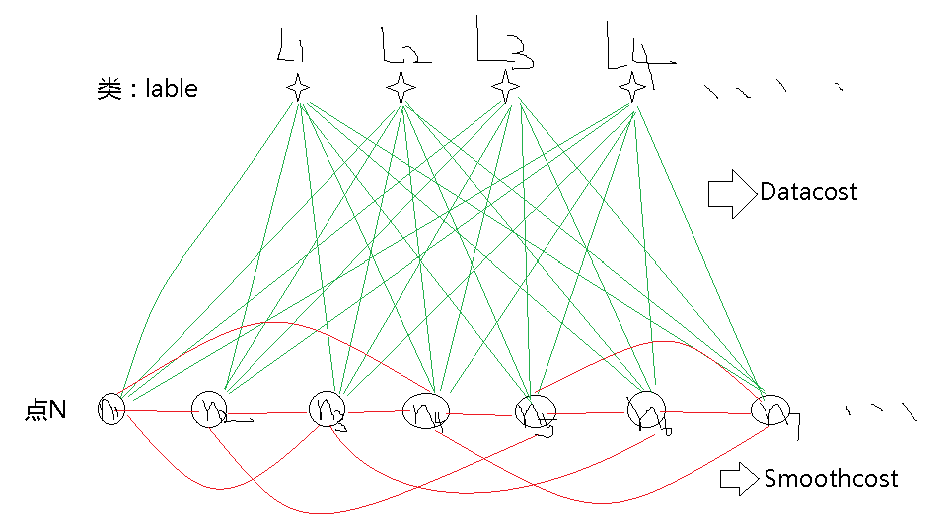
可以看到的datacost，这里每个datacost计算方式为

(Ip−Ic)2

函数如下：

function datacost = Datacost1(img,ctrs)
[m,n] = size(img);
num_lables = size(ctrs,1);
totalsizes = m*n;
datacost = zeros(totalsizes,num_lables);
for i = 1:totalsizes
    Ip = double(img(i));
    for j = 1:num_lables
         datacost(i,j) = (Ip - ctrs(j)).^2;  %计算datacost项
    end
End

三）点与点之间的权值-neighbours

这一项描述的是一个领域项，认为每个点与周围的四领域或者8领域内的像素点有联系（也就是边权值有值），与其他剩下的所有点没有关系（边权值为0），相邻的像素点之间的边权值大小的计算方式为：

Bpq=e−(Ip−Iq)22σ

式中，sigma为整幅图像的方差。看过前面的知道，这个矩阵是相当的大（(m*n)*(m*n)）(m,n图像大小)，且是个稀疏矩阵，要是每个元素都储存起来根本储存不下来，这里以稀疏矩阵的方法储存。
生成该权值矩阵的函数如下：

%%------------------- %  每个点的灰度作为特征
%%------------------- function Neighbours = neighbours1(img) [m,n] = size(img); totalsizes = m*n; var_img = var(img(:)); %图像方差
%% 选择neigh=4四连通计算权值，neigh=8八连通计算权值 neigh = 4; %%
if neigh == 4
    %构建索引向量--生成距离的稀疏矩阵
    i1 = (1:totalsizes-m)'; j1 = i1+m; for i = 1:n i2_tem(:,i) = (i-1)*m + (1:m-1)';
    end
    i2 = i2_tem(:);
    j2 = i2+1;
    %对应边的值
    ans1 = exp(-(img(i1(:))-img(j1(:))).^2/(2*var_img));
    ans2 = exp(-(img(i2(:))-img(j2(:))).^2/(2*var_img));
    %组合相应的向量：x位置，y位置，权值（注意必须都是列向量）
    all = [[i1;i2],[j1;j2],[ans1;ans2]];
else
    %构建索引向量--生成距离的稀疏矩阵
    i1 = (1:totalsizes-m)'; %正右权值 j1 = i1+m; for i = 1:n %正下权值 i2_tem(:,i) = (i-1)*m + (1:m-1)';
    end
    i2 = i2_tem(:);
    j2 = i2+1;
    for i = 1:n-1  %斜下权值
        i3_tem(:,i) = (i-1)*m + (1:m-1)'; end i3 = i3_tem(:); j3 = i3+n+1; i4 = i3+1; %斜上权值 j4 = i3+m; %对应边的值 ans1 = exp(-(img(i1(:))-img(j1(:))).^2/(2*var_img)); ans2 = exp(-(img(i2(:))-img(j2(:))).^2/(2*var_img)); ans3 = exp(-(img(i3(:))-img(j3(:))).^2/(2*var_img)); ans4 = exp(-(img(i4(:))-img(j4(:))).^2/(2*var_img)); %组合相应的向量：x位置，y位置，权值（注意必须都是列向量） all = [[i1;i2;i3;i4],[j1;j2;j3;j4],[ans1;ans2;ans3;ans4]]; end %matlab函数生成稀疏矩阵（这么做的速度最快） %---------------- neighb = spconvert(all); neighb(totalsizes,totalsizes) = 0; Neighbours = neighb;

再有就是上一个博客说到，这个工具箱的实际点与点之间的权值大小并不是单纯的Neighbours，而是在Neighbours 基础上乘以一个SmoothCost，这里为了直接使用到Neighbours，将SmoothCost设置为1即可。而这就是potts模型。相关设置：

%设置smoothcost
%不设置的时候默认使用potts模型
SmoothCost = eye(Numlables);
SmoothCost = 1 - SmoothCost;
GCO_SetSmoothCost(h,SmoothCost);

四）可以开始了

在设置好了相关权值参数后，剩下的就是把这些组合起来了。前面说过，图割是以能量函数的方式最小化方式进行的，当所有部分的能量达到最小的时候输出最优结果（图割得到的结果当然也只是一个局部最优解，因为这个分割问题也是一个NP难问题，因此每一次运行的最终能量值不一样，但是也不能差太多）。像上述的我们只涉及到了两类能量，一个是点与类之间不同的一个能量，一个是点与点（领域项）之间不同的一个能量，而这两个能量我们再用一个potts模型参数来控制他们之间的比例关系，这个比例关系也决定了最后分割的样子。试着从理论上去分析一下，点与点（领域项）之间的这个能量其实是控制局部平滑的一个约束项，如果这一项能量占比重越大，认为分割图像之间就应该越平滑，那么带来的分割效果就是图像分割的越光滑，而这又带来的另一个问题就是图像的细节保留的就少了，怎么权衡这个参数就是需要进一步研究的地方。下面给出综合起来的主程序：

clc;
clear;
%读取图像
img = imread('lena.jpg');
img = double(rgb2gray(img));
%定义分类数 Numlables
Numlables = 5;
%定义Potts模型参数K
Potts_K = 100;

[m,n] = size(img);
totalsizes = m*n;
%k-means预分类找到中心与分类
%init_lable预分类，列向量； ctrs-类中心灰度值值
[init_lable,ctrs] = kmeans(img(:),Numlables); %img通过索引转化为列向量可用
ctrs_new = zeros(Numlables,1);

%生成目标体
h = GCO_Create(totalsizes,Numlables);
%设置初始标签
%% 已知初始化
GCO_SetLabeling(h,init_lable);

%设置datacost项
datacost = Datacost1(img,ctrs);
datacost = datacost';
GCO_SetDataCost(h,datacost);

%设置smoothcost
%不设置的时候默认使用potts模型
SmoothCost = eye(Numlables);
SmoothCost = 1 - SmoothCost;
GCO_SetSmoothCost(h,SmoothCost);

%设置neighbors项
Neighbours = Potts_K*neighbours1(img);
GCO_SetNeighbors(h,Neighbours);

%显示输出结果
GCO_SetVerbosity(h,2);
%类标签运算顺序
GCO_SetLabelOrder(h,randperm(Numlables));
%膨胀算法
GCO_Expansion(h);
%获得该标签lables
Labeling = GCO_GetLabeling(h);  %列向量

% 释放内存
GCO_Delete(h);
%显示graph cut分类
for i = 1:length(Labeling)
img1(i) = ctrs(Labeling(i));
end
img1 = reshape(img1,m,n);
%%
%绘制分割图
figure;
%原图像
subplot(1,2,1);imshow(img,[]);
title('原始图像');
%显示graph cut分类
subplot(1,2,2);imshow(img1,[]);
title(['Potts模型参数:',num2str(Potts_K)]);     

五）实验结果

potts模型参数的不同带来图像的分割效果不同，下面给出potts模型参数从100-2000之间的过程中的运行结果：






这是一次运行过程中的能量值变化：

gco>> starting alpha-expansion w/ adaptive cycles
gco>> initial energy:   E=8459828 (E=6728394+1731434+0)
gco>>   after expansion(4):     E=8378569 (E=6778690+1599879+0);     50177 vars;    (1 of 5);    23.75 ms
gco>>   after expansion(5):     E=8357847 (E=6793528+1564319+0);     52615 vars;    (2 of 5);    23.76 ms
gco>>   after expansion(2):     E=8340678 (E=6806374+1534304+0);     56583 vars;    (3 of 5);    28.67 ms
gco>>   after expansion(3):     E=8307729 (E=6832920+1474809+0);     52857 vars;    (4 of 5);    30.01 ms
gco>>   after expansion(1):     E=8264986 (E=6866636+1398350+0);     48939 vars;    (5 of 5);    23.84 ms
gco>> after cycle  1:   E=8264986 (E=6866636+1398350+0);    5 expansions(s);
gco>>   after expansion(4):     E=8264958 (E=6866999+1397959+0);     49960 vars;    (1 of 5);    23.78 ms
gco>>   after expansion(5):     E=8264958 (E=6866999+1397959+0);     52571 vars;    (2 of 5);    23.74 ms
gco>>   after expansion(1):     E=8264958 (E=6866999+1397959+0);     48394 vars;    (3 of 5);    22.35 ms
gco>>   after expansion(3):     E=8264958 (E=6866999+1397959+0);     52498 vars;    (4 of 5);    28.39 ms
gco>>   after expansion(2):     E=8264958 (E=6866999+1397959+0);     56684 vars;    (5 of 5);    28.51 ms
gco>> after cycle  2:   E=8264958 (E=6866999+1397959+0);    5 expansions(s);
gco>>   after expansion(4):     E=8264958 (E=6866999+1397959+0);     49953 vars;    (1 of 1);    26.76 ms
gco>> after cycle  3:   E=8264958 (E=6866999+1397959+0);    1 expansions(s);
gco>>   after expansion(2):     E=8264958 (E=6866999+1397959+0);     56684 vars;    (1 of 4);    26.40 ms
gco>>   after expansion(5):     E=8264958 (E=6866999+1397959+0);     52571 vars;    (2 of 4);    24.81 ms
gco>>   after expansion(1):     E=8264958 (E=6866999+1397959+0);     48394 vars;    (3 of 4);    27.76 ms
gco>>   after expansion(3):     E=8264958 (E=6866999+1397959+0);     52498 vars;    (4 of 4);    24.38 ms
gco>> after cycle  4:   E=8264958 (E=6866999+1397959+0);    4 expansions(s);

六）到总结了

从上面的结果可以看出，potts模型参数越大，带来的图像分割越平滑，对细节的保留就越少，而对于基础图割算法的改进方法一般就是对这两个能量函数进行改进，改进能量函数的边权值计算方法，能量函数的构造方法，能量函数的寻优方式等等，当然很多问题还得就实际问题实际分析，分割方法没有最好，只有更适合，其实也有最好，那就是人眼分割–计算机视觉与人工智能的终极目标……