OpenCASCADE Make Primitives-Box
eryar@163.com
Abstract. By making a simple box to demonstrate the BRep data structure of the OpenCASCADE. The construction method is different from BRepPrimAPI_MakeBox. In the paper construct the box from vertex, edge to solid, while in BRepPrimAPI_MakeBox from solid, shell to vertex. From the construction, the BRep data structure in OpenCASCADE also can be called the Winged-Edge data structure.
Key Words. OpenCASCADE, BRep, Box, The Winged-Edge Structure
1. Introduction
OpenCASCADE的Toolit TKPrim中提供了基本图元的创建功能,像Box, Cylinder, Sphere等等。直接使用Package BRepPrimAPI中的功能,可以方便地创建出基本图元,而不用关心其内部的数据结构。
Figure 1. BRepPrimAPI Package classes
为了理解ModelingData模块中OpenCASCADE的边界表示法BRep数据结构,决定参考其实现,自己来创建出基本图元,进而理解其中的BRep数据结构。本文以最简单的长方体Box入手,从点、边到体的创建出一个形状。并将构造的形状在Draw Test Harness中进行显示,且进行布尔运算,来验证构造结果的正确性。
2.Make a Face of the Box
在OpenCASCADE的包BRepPrim中,构造长方体的方式是形状的根结点出发到叶子结点,即从Shell到Face到Wire最后到Vertex,如下图所示:
Figure 2.1 Data structure of a Shape
为了程序演示的清晰,本文中采用与OpenCASCADE中相反的方式,即先从叶子结点出发,逐步回到根结点,即先构造出顶点、边最后到实体。长方体由六个面构成,所以先从一个面开始来构造。将一个面构造成功后,其他六个面的构造方法就相同了。
构造使用了BRep_Builder,在创建相应的拓朴的同时可以将其相关的几何信息设置进去。如创建顶点Vertex时,可以将点的坐标信息及容差值设置进去,代码如下所示:
// make vertex of the box.
aBuilder.MakeVertex(aVertices[ 0 ], aPoints[ 0 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 1 ], aPoints[ 1 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 2 ], aPoints[ 2 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 3 ], aPoints[ 3 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 4 ], aPoints[ 4 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 5 ], aPoints[ 5 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 6 ], aPoints[ 6 ], Precision::Confusion());
aBuilder.MakeVertex(aVertices[ 7 ], aPoints[ 7 ], Precision::Confusion());
创建边的同时,将其边中的三维曲线信息也设置进去,代码如下所示:
aBuilder.MakeEdge(aEdges[ 0 ], new Geom_Line(aLines[ 0 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 1 ], new Geom_Line(aLines[ 1 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 2 ], new Geom_Line(aLines[ 2 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 3 ], new Geom_Line(aLines[ 3 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 4 ], new Geom_Line(aLines[ 4 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 5 ], new Geom_Line(aLines[ 5 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 6 ], new Geom_Line(aLines[ 6 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 7 ], new Geom_Line(aLines[ 7 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 8 ], new Geom_Line(aLines[ 8 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 9 ], new Geom_Line(aLines[ 9 ]), Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 10 ], new Geom_Line(aLines[ 10 ]),Precision::Confusion());
aBuilder.MakeEdge(aEdges[ 11 ], new Geom_Line(aLines[ 11 ]),Precision::Confusion());
创建的边Edge还需要与顶点Vertex关联上,且需要注意顶点的反向,示例代码如下所示:
// edge 0:
{
TopoDS_Vertex V1 = aVertices[ 0 ];
TopoDS_Vertex V2 = aVertices[ 1 ];
V2.Reverse();
aBuilder.Add(aEdges[ 0 ], V1);
aBuilder.Add(aEdges[ 0 ], V2);
aBuilder.UpdateVertex(V1, ElCLib::Parameter(aLines[ 0 ], aPoints[ 0 ]),
aEdges[ 0 ], Precision::Confusion());
aBuilder.UpdateVertex(V2, ElCLib::Parameter(aLines[ 0 ], aPoints[ 1 ]),
aEdges[ 0 ], Precision::Confusion());
BRepTools::Update(aEdges[ 0 ]);
}
接着创建Wire,创建Wire时需要注意边的反向,从而构造成一个闭合的Wire,代码如下所示:
aBuilder.MakeWire(aWires[ 0 ]);
// wire 1: bottom
{
TopoDS_Edge E1 = aEdges[ 0 ];
TopoDS_Edge E2 = aEdges[ 1 ];
TopoDS_Edge E3 = aEdges[ 2 ];
TopoDS_Edge E4 = aEdges[ 3 ];
E3.Reverse();
E4.Reverse();
aBuilder.Add(aWires[ 0 ], E1);
aBuilder.Add(aWires[ 0 ], E2);
aBuilder.Add(aWires[ 0 ], E3);
aBuilder.Add(aWires[ 0 ], E4);
BRepTools::Update(aWires[ 0 ]);
}
关键是面的创建及面创建后,设置边与面的关联信息,即PCurve的信息。如果没有PCurve的信息,可视化显示就不能正确显示出面,即网格化算法会失败。长方体底面的创建及PCurve设置代码如下所示:
aBuilder.MakeFace(aFaces[ 0 ], new Geom_Plane(aPlanes[ 0 ]),Precision::Confusion());
aBuilder.Add(aFaces[ 0 ], aWires[ 0 ]);
// set bottom pcurve info of between the edge and surface.
{
// pcurve 0:
double u = 0.0 ;
double v = 0.0 ;
double du = 0.0 ;
double dv = 0.0 ;
gp_Dir DX = aPlanes[ 0 ].XAxis().Direction();
gp_Dir DY = aPlanes[ 0 ].YAxis().Direction();
ElSLib::Parameters(aPlanes[ 0 ], aLines[ 0 ].Location(), u, v);
du = aLines[ 0 ].Direction() * DX;
dv = aLines[ 0 ].Direction() * DY;
aBuilder.UpdateEdge(aEdges[ 0 ], new Geom2d_Line(gp_Lin2d(gp_Pnt2d(u, v),
gp_Dir2d(du, dv))), aFaces[ 0 ], Precision::Confusion());
// pcurve 1:
ElSLib::Parameters(aPlanes[ 0 ], aLines[ 1 ].Location(), u, v);
du = aLines[ 1 ].Direction() * DX;
dv = aLines[ 1 ].Direction() * DY;
aBuilder.UpdateEdge(aEdges[ 1 ], new Geom2d_Line(gp_Lin2d(gp_Pnt2d(u, v),
gp_Dir2d(du, dv))), aFaces[ 0 ], Precision::Confusion());
// pcurve 2:
ElSLib::Parameters(aPlanes[ 0 ], aLines[ 2 ].Location(), u, v);
du = aLines[ 2 ].Direction() * DX;
dv = aLines[ 2 ].Direction() * DY;
aBuilder.UpdateEdge(aEdges[ 2 ], new Geom2d_Line(gp_Lin2d(gp_Pnt2d(u, v),
gp_Dir2d(du, dv))), aFaces[ 0 ], Precision::Confusion());
// pcurve 3:
ElSLib::Parameters(aPlanes[ 0 ], aLines[ 3 ].Location(), u, v);
du = aLines[ 3 ].Direction() * DX;
dv = aLines[ 3 ].Direction() * DY;
aBuilder.UpdateEdge(aEdges[ 3 ], new Geom2d_Line(gp_Lin2d(gp_Pnt2d(u, v),
gp_Dir2d(du, dv))), aFaces[ 0 ], Precision::Confusion());
}
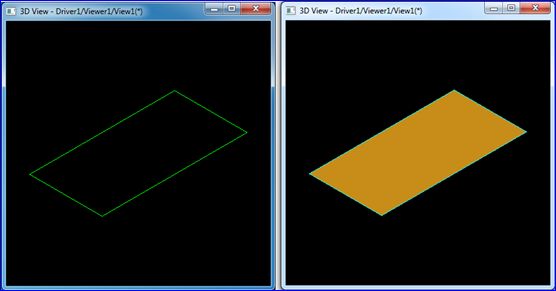
历经艰辛,最后终于将一个面创建出来了,且可以在Draw Test Harness中显示,如下图所示:
Figure 2.2 A Face of the Box in Draw Test Harness
如上图所示,在Darw Test Harness中,边的颜色是有讲究的,说明如下:
In Draw Test Harness, shapes are displayed using isoparametric curves. There is color coding for the Edges:
v A red edge is an isolated edge, which belongs to no faces;
v A green edge is a free boundary edge, which belongs to one face;
v A yello edge is shared edge, which belongs to at least two faces;
Figure 2.3 Color Coding for Edges in Draw Test Harness
如上图所示,红色的边表示此边不属于任何一个面;绿色的边表示此边只属于一个面;黄色的面表示此面至少属于两个面。
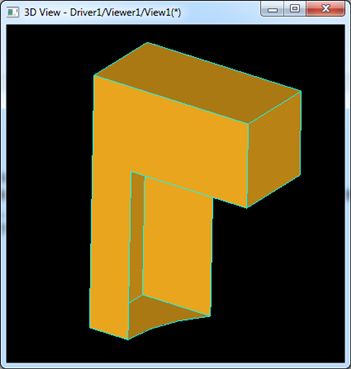
Figure 2.4 Shared Edges of the Box
如上图所示,当创建出长方体的三个面时,侧面与上下两个底面相连的边显示成了黄色。其他边都是绿色。
3.Finish the Box
将长方体的六个面按上述方式创建完毕后,需要验证其正确性。于是将生成的数据导出为Brep格式,并与其他基本体进行布尔运算。
当导出的长方体为Shell时进行布尔运算会得到的也是壳体,如下图所示的结果:
Figure 3.1 Box Shell Cut a Cylinder
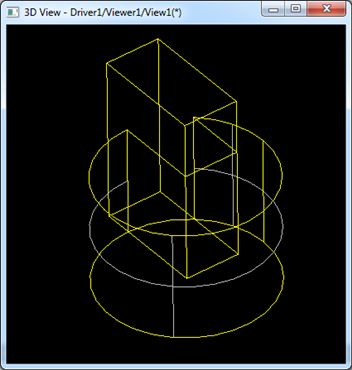
当导出的长方体为Solid时,若面的方式未正确设置,则布尔运算会失败,如下图所示:
Figure 3.2 Box Solid Cut a Cylinder
如上图所示,长方体与圆柱体的交线都已经计算出来了,但由于面的方向不对,不知道去除哪些面,保留哪些面。
将面的方向正确设置后,导出为Solid,进行布尔运算,结果正确,如下图所示:
Figure 3.3 Box Cut Cylinder
测试用的Tcl脚本代码如下所示:
# Tcl script to test the box BRep data.
# eryar@163.com
# 2014-11-16 21:55
# OpenCASCADE6.8.0
#
pload ALL
restore d :/ box . brep b
pcylinder c 1.5 2
bop b c
bopcut r
vdisplay r
4.Conclusion
通过创建基本图元,从而进一步来理解OpenCASCADE中的边界表示BRep的数据结构。需要注意的事项有:
v 创建边时,需要设置边中几何曲线的范围;
v 创建边时,需要设置正确与边相关顶点的方向;
v 创建环时,需要确保环中边的参数曲线PCurve能在参数空间中闭合;
v 创建面后,需要在边中设置与面相关的几何信息;
v 创建体时,需要所有面的方向正确;
注:最后发现前不久写的一篇文章有误,说OpenCASCADE的BRep不是翼边结构。其实从边出发是可以找到与点、面相关的信息的。因为OpenCASCADE中拓朴结构中有包含关系,所以顶点信息已经包含在边中了,直接遍历边即可得到与此边相关的顶点信息。所以,这样看来OpenCASCADE中的BRep表示法也是翼边的数据结构。
原文如下:
边界表示方式比较。因为一般的书籍上都详细重点描述了边界表示中以为边为核心的翼边数据结构,所以有人想从这方面来给OpenCASCADE中的Brep表示法来给个说法。结合上面的类图可知,从边出发并不能访问到与这条边相关的其他信息,如顶点的信息。如果硬是想在这里给个名分,倒是从点出发可以找到边及面的几何信息,所以OpenCASCADE中的Brep表示法应该更像是以点为基础的表示方法。OpenNURBS中通过ON_BrepTrim,可以访问其他的信息,而ON_BrepTrim与边ON_BrepEdge的意义有些相似,所以应该是以边为核心的翼边结构了。
5. References
1. OpenCASCADE BRep vs. OpenNURBS Brep. OpenCASCADE BRep vs. OpenNURBS BRep
PDF Version and Source Code: OpenCASCADE Make Primitives-Box