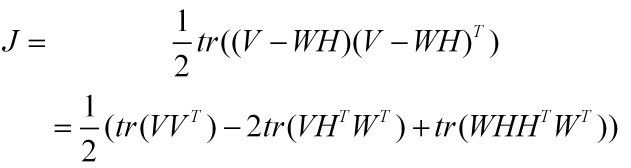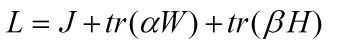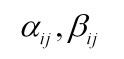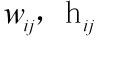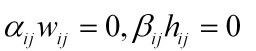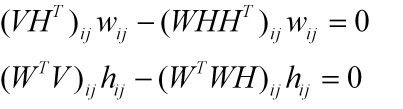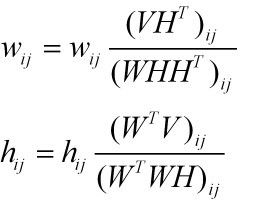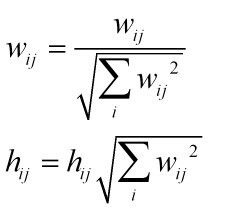NMF学习

NMF：非负矩阵因式分解。 NMF一直被认为是对多维数据分解的一个很有效的方法，包括在聚类和推荐系统中应用等。

NMF矩阵算法介绍：

给定一个非负矩阵V，我们可以找到2个非负分解因子矩阵W，H.其中，W称为权重矩阵，H称为特征矩阵。公式如下：

当n维数据向量集放置在n*m的矩阵V中，其中m是数据集的大小。V分解的的权重矩阵W：n*r；V分解的特征矩阵H： r*m； 通常r小于n，m。 r表示采用的特征数。这个可以认为是一种数据压缩方法。

这里，关键为题是如何计算出W，H矩阵？

首先我们构造一个代价函数：

代价函数J可以重写为：

这是个典型的优化问题，这里采用拉格朗日乘法去优化J。

构造拉格朗日函数L：

说明如下：W，H的每个元素必须大于等于0，这样设置

为

拉格朗日乘法因子。其中

。

这样，做L对W，H进行求偏导如下：

根据KKT条件：

所以，得到如下：

根据以上等式，我们可以得出一个乘法迭代更新公式：

到目前为止，我们基本上描述完了利用乘法更新规则求解NMF的过程。

其实，可以看出来，根据上面的规则：W，H不是唯一的。

若果想使W，H唯一，我们可以设定（当然这只是其中一种假设方法）W的列向量欧式距离长度为1，就对W进行列的归一化处理：

参考文献：

【1】Daniel D. Lee. Algorithms for Non-negative Matrix Factorization

【2】Wei Xu, Xin Liu, Yihong Gong.Document Clustering Based On Non-negative Matrix Factorization