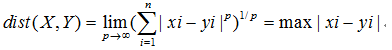NLP(二)--编辑距离
编辑距离,又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。
许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
例如将kitten一字转成sitting:
sitten (k→s)
sittin (e→i)
sitting (→g)
俄罗斯科学家Levenshtein在1965年提出这个概念。
考虑长度为n1,n2的两个字符串S1,S2.
如果已知长度为I-1,j-1的两个子字符串S1[1],S1[2]…S1[i-1]; S2[1],S2[2]…S2[j-1].编辑距离为D[i-1][j-1].
考虑长为i,j的两个子串.
如果s1[i]!=s2[j],我们可以做如下操作:
1. 删除s1[i]
2. 删除s2[j]
3. 改变s1[i]为s2[j]
4. 改变s2[j]为s1[i]
如果s1[i]==s2[j],那么D[i][j]=D[i-1][j-1];
归纳一下就是:
S1[i]==S2[j]?
D[i][j]=max(D[i-1][j],D[i][j-1],D[i-1][j-1])+1;
Else
D[i][j]=D[i-1][j-1];
那么解法就有:
1.递归,不过开销太大,重复计算太多.
2.加入动态数组存储中间变量,以空间换时间,就是动态规划的算法.
动态规划代码:
#include<iostream>
using namespace std;
#define MAX 3000
char s1[MAX];
char s2[MAX];
int F[MAX][MAX];
int min(int a,int b,int c)
{
if(a<=b&&a<=c)
return a;
if(b<=a&&b<=c)
return b;
return c;
}
int dis(char *s1,char *s2)
{
int len1=strlen(s1);
int len2=strlen(s2);
if(len1==0||len2==0)
{
return max(len1,len2);
}
for(int i=0;i<=len1;i++)
{
F[i][0]=i;
}
for(int j=0;j<=len2;j++)
{
F[0][j]=j;
}
for(int i=1;i<=len1;i++)
{
for(int j=1;j<=len2;j++)
{
if(s1[i-1]==s2[j-1])
F[i][j]=F[i-1][j-1];
else
F[i][j]=min(F[i][j-1],F[i-1][j],F[i-1][j-1])+1;
}
}
return F[len1][len2];
}
int main()
{
scanf("%s",&s1);
getchar();
scanf("%s",&s2);
printf("%d\n",dis(s1,s2));
return 0;
}
为什么要引入编辑距离?
记得有一篇关于距离与相似性度量的blog,列举了一些如欧式距离,余弦夹角,KL相对熵等.
(blog: http://blog.csdn.net/ice110956/article/details/14143991 ).
上述这些距离,有一些是基于统计的变量与向量之间的距离.显然,我们在判断字符串相似度的时候,貌似没有必要引入统计信息.如:
字符串ABCD与EFGH的皮尔森相关系数为0,不过就字符串来说,貌似没有特别大的关系.
没有统计相关的距离,我们用什么来衡量呢?想到一个距离--切比雪夫距离.
公式为:
这种距离有何意义?看到引出切比雪夫距离的具体问题时,我发现,某个距离在特定的场合下时候,是恰如其分的.
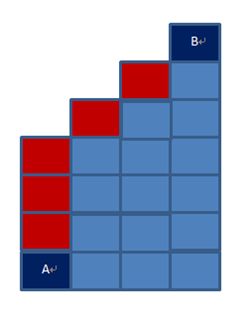
切比雪夫距离起源于国际象棋中国王的走法,我们知道国际象棋国王每次只能往周围的8格中走一步,那么如果要从棋盘中A格(x1, y1)走到B格(x2, y2)最少需要走几步?
假设下面是棋盘的一小块,国王要从A到B,只能横,竖,斜地走.那么无论怎么走,最短距离始终是7=max(4,7);
再来看编辑距离,我们书写文字的时候,特别是英文的时候,容易写错,漏写,多写几个字母.那么修改为正确的单词,不外乎三个方法:改写,删除,增加.这样的操作越少,书写的越正确.
再联系编辑距离的”编辑”二字,就有了关于编辑距离直观上的理解.
编辑距离可以有如下的运用:
纠错
(就像我们前面举得例子,通过改写,删除,增加最少化来纠错)
DNA分析
抄袭检测
(通过两篇文章的编辑距离来检测是否抄袭,当然,应该还有更好的方法)
语音辨识
文本纠错
简单介绍下其中一个运用,文本纠错.
按照上面的叙述,假设一个错误拼写A,如何在字典中找出编辑距离最小的正确拼写A’?暴力法就是遍历字典.
下面的方法参考matrix67.com.
度量空间:
度量空间是二元组 (M,d),这里的 M 是集合, d 是在 M 上的度量(metric),就是函数
存在:
d(x, y) ≥ 0 (非负性)
d(x, y) = 0 当且仅当x = y (不可区分者的同一性)
d(x, y) = d(y, x) (对称性)
d(x, z) ≤ d(x, y)+ d(y, z) (三角不等式)。
三维空间就是典型的度量空间,d定义为两点间的距离.
BK树.
BK树是一棵度量树,用于离散度量空间.用d(A,B)表示A,B之间的距离.
建树:以任意元素为头结点建树,其第k个子树为d(A,X)==k的元素.递归建树.
通过上述方式建立的BK字典树,可以用于有效地查找与某个元素距离为k的所有元素.
查询:比如要查询与A距离为n的所有字符串.
从头结点开始,如果A与头结点d为k,那么问题转而变为与头结点距离为k-n和k+n的字符串.递归查询,直到叶子节点
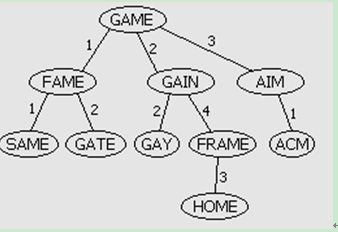
偷一张使用编辑距离建立好的BKtrie如下:
“ 实践表明,一次查询所遍历的节点不会超过所有节点的5%到8%,两次查询则一般不会17-25%,效率远远超过暴力枚举。适当进行缓存,减小Levenshtein距离常数n可以使算法效率更高。”