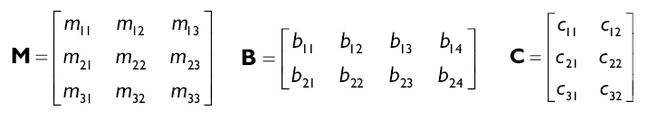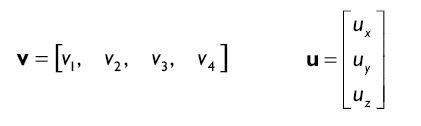D3D编程必备的数学知识(3)
矩阵
在这一部分我们关注的焦点是数学中的矩阵。它们在3D图形学中的应用将在下一部分讲解。
一个m×n的矩阵是由m行和n列的数字组成的矩阵列。行和列的数字就是这个矩阵的维数。我们通过写在下方的数字识别矩阵清单,数字中的第一个表示行第二个表示列。例如下边的M是3×3矩阵,B是2×4矩阵, C是3×2矩阵。
我们使用加粗的大写字母表示矩阵。有时一个矩阵只包含一行或者一列。我们用行矩阵和列矩阵这个特殊的名称来称呼。例如下边就是行和列矩阵:
当使用行或列矩阵时,我们只用一个下标,有时我们还用字母表示。
D3DX 矩阵
当设计Direct3D应用程序时,使用4×4矩阵和1×4行矩阵(向量)是有代表性的。注意使用这两种矩阵意味着可以进行下列定义的矩阵乘法。
n 向量-矩阵乘法。即,假如1×4的单行矩阵V,和4×4的矩阵T,那么积VT可计算并且返回的结果是一个1×4的单行矩阵(向量)。
n 矩阵-矩阵乘法。即,假如4×4的矩阵T,和4×4的矩阵R,那么积TR和RT可计算并且两者返回的结果都是一个4×4的矩阵。注意因为矩阵乘法不满足交换律所以TR和RT不一定相等。
在D3DX中表示1×4的行矩阵(向量),我们用D3DXVECTOR3和D3DXVECTOR4向量类。当然D3DXVECTOR3只有3个成员,不是4个。然而,第4个成员缺省是1或0(在下一部分有更多信息)。
在D3DX中表示4×4的矩阵,我们用D3DXMATRIX类,定义如下:
typedef struct D3DXMATRIX : public D3DMATRIX
{
public:
D3DXMATRIX() {};
D3DXMATRIX(CONST FLOAT*);
D3DXMATRIX(CONST D3DMATRIX&);
D3DXMATRIX(FLOAT _11, FLOAT _12, FLOAT _13, FLOAT _14,
FLOAT _21, FLOAT _22, FLOAT _23, FLOAT _24,
FLOAT _31, FLOAT _32, FLOAT _33, FLOAT _34,
FLOAT _41, FLOAT _42, FLOAT _43, FLOAT _44);
// access grants
FLOAT& operator () (UINT Row, UINT Col);
FLOAT operator () (UINT Row, UINT Col) const;
// casting operators
operator FLOAT* ();
operator CONST FLOAT* () const;
// assignment operators
D3DXMATRIX& operator *= (CONST D3DXMATRIX&);
D3DXMATRIX& operator += (CONST D3DXMATRIX&);
D3DXMATRIX& operator -= (CONST D3DXMATRIX&);
D3DXMATRIX& operator *= (FLOAT);
D3DXMATRIX& operator /= (FLOAT);
// unary operators
D3DXMATRIX operator + () const;
D3DXMATRIX operator - () const;
// binary operators
D3DXMATRIX operator * (CONST D3DXMATRIX&) const;
D3DXMATRIX operator + (CONST D3DXMATRIX&) const;
D3DXMATRIX operator - (CONST D3DXMATRIX&) const;
D3DXMATRIX operator * (FLOAT) const;
D3DXMATRIX operator / (FLOAT) const;
friend D3DXMATRIX operator * (FLOAT, CONST D3DXMATRIX&);
BOOL operator == (CONST D3DXMATRIX&) const;
BOOL operator != (CONST D3DXMATRIX&) const;
} D3DXMATRIX, *LPD3DXMATRIX;
The D3DXMATRIX class inherits its data entries from the simpler D3DMATRIX structure, which is defined as:
typedef struct _D3DMATRIX {
union {
struct {
float _11, _12, _13, _14;
float _21, _22, _23, _24;
float _31, _32, _33, _34;
float _41, _42, _43, _44;
};
float m[4][4];
};
} D3DMATRIX;
观察D3DXMATRIX类发现有很多有用的运算符,比如对矩阵检测相等,矩阵相加和矩阵相减,标量与矩阵相乘,类型转换(casting),以及非常重要的两个D3DXMATRIXs相乘。因为矩阵相乘是非常重要的,我们给出一段实例代码:
| D3DXMATRIX A(…); // initialize A D3DXMATRIX B(…); // initialize B D3DXMATRIX C = A * B; // C = AB |
D3DXMATRIX类另一个重要的运算符是小括号,它允许我们非常方便的为矩阵成员赋值。注意当使用小括号时我们的下标就象C语言数组下标一样是从0开始的。例如,为一个矩阵的ij = 11 赋值,我们写成:
| D3DXMATRIX M; M(0, 0) = 5.0f; // Set entry ij = 11 to 5.0f. |
D3DX库也提供下列有用的函数:将D3DXMATRIX转化为单位矩阵,转置D3DXMATRIX矩阵以及求逆矩阵。
D3DXMATRIX *D3DXMatrixIdentity(
D3DXMATRIX *pout // 将矩阵转换为单位矩阵
);
| D3DXMATRIX M; D3DXMatrixIdentity( &M ); // M = 单位矩阵 |
D3DXMATRIX *D3DXMatrixTranspose(
D3DXMATRIX *pOut, // 输出的转置矩阵
CONST D3DXMATRIX *pM // 原矩阵
);
| D3DXMATRIX A(...); // 初始化矩阵A D3DXMATRIX B; D3DXMatrixTranspose( &B, &A ); // B = 输出的转置矩阵 |
假如我们将不能求逆的矩阵用求逆函数,那么函数将会返回null.同样的,这本书我们忽视第二个参数,并且总是把它设置为0。
D3DXMATRIX *D3DXMatrixInverse(
D3DXMATRIX *pOut, // 输出的逆矩阵
FLOAT *pDeterminant, // 除非是必需的,一般设为0
CONST D3DXMATRIX *pM // 原矩阵
);
| D3DXMATRIX A(...); // 初始化矩阵 D3DXMATRIX B; D3DXMatrixInverse( &B, 0, &A ); // B = A的逆矩阵 |