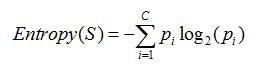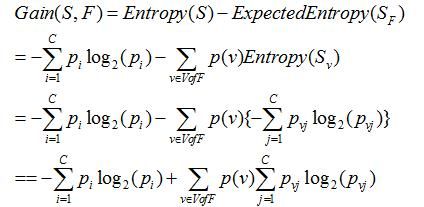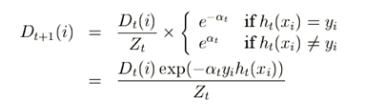决策树理论、C4.5源码分析及AdaBoost算法的提升改造
http://www.tuicool.com/articles/2Inaam
第一部分 决策树
一、决策树原理
示例:
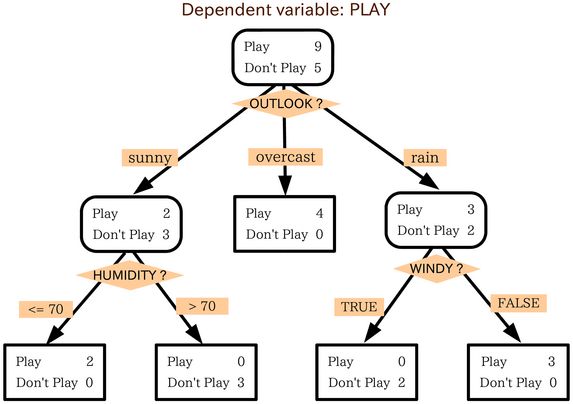
决策树可分为分类树和回归树两种。分类树的叶节点对应于一个类别。回归书的叶节点对应于一连续值。
经典的决策树有ID3、C4.5、C5.0(由RossQuinlan发明,属于分类树)以及CART(分类回归树)。
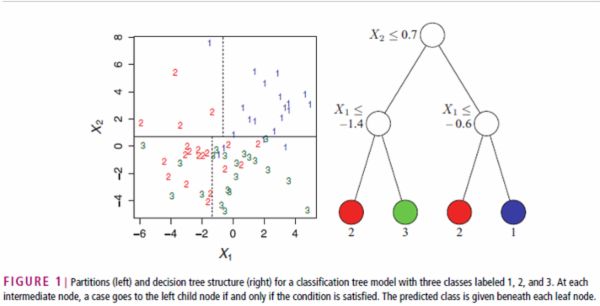
决策树的基本思想是空间划分,通过递归的方式把关于自变量的m维空间划分为不重叠的矩形。如图所示,决策树首先按X2是否大于0.7将空间划分为两部分,然后再在这两部分分别按X1划分空间。整个空间被划分为四个矩形,各自对应一个分类结果。
二、属性划分依据
ID3、C4.5、CART进行空间划分的依据分别是信息增益、信息增益率、Gini指标。
1. 信息熵
香农发明的,用于解决对系统信息的度量量化问题,可以理解为信息量。当系统很纯时,其度量值应为0。一个系统越是有序,信息熵就越低;反之,一个系统越乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个衡量。计算公式是
其中,Pi表示第i个类的概率,也即属于类i的样本比例。
2. 信息增益
指期望信息或者信息熵的有效减少量。可理解为前后信息的差值,在决策树分类问题中,即就是决策树在进行属性选择划分前和划分后的信息差值。
条件熵:计算当一个特征t不能变化时,系统的信息量是多少。
其中,v是特征T的多种取值,p(v)是每个特征取值的概率,Pvj是指定特征取值时各类的概率。
ID3选择最大的信息增益属性来进行划分。
3. 信息增益率
使用信息增益的划分方法,存在由划分个数引起的偏置问题。假设某个属性存在大量的不同值,在划分时将每个值成为一个结点。最终计算得到划分后的信息量为: i n o ( 1 , … , n ) = ∑ni = 1 | i || | × e n t r o p ( i ) = 0 。因为 e n t r o p ( i ) = i n o ( [ 1 , 0 ] ( 或 i n o ( [ 0 , 1 ] ) ,只含一个纯结点。这样决策树在选择属性时,将偏向于选择该属性,但这肯定是不正确(导致过拟合)的。因此有必要使用一种更好的方法,那就是C4.5中使用的信息增益率(Info Gain Ratio),其考虑了分支数量和尺寸的因素,使用称为内在信息(Intrinsic Information)的概念。
内在信息(Intrinsic Information),可简单地理解为表示信息分支所需要的信息量,其计算公式如下:
信息增益率则计算如下:
4. Gini系数
用来度量数据集的不纯度:
i n i ( ) = 1 − ∑j = 1n p2j
其中, pj 是类j在T中的相对频率,当类在T中是倾斜的时,gini(T)会最小。
将T划分为T1(实例数为N1)和T2(实例数为N2)两个子集后,划分数据的Gini定义如下:
然后选择其中最小的 i n is p l i t ( ) 作为结点划分决策树。
三、建树和剪枝
1. ID3
ID3选择具有最高信息增益的属性作为测试属性。算法如下:
2. C4.5
C4.5选择最高信息增益率的属性作为测试属性。
连续值属性的离散化处理:把需要处理的样本(对应根节点)或样本子集(对应子树)按照连续变量的大小从小到大进行排序;假设该属性对应的不同的属性值一共有N个,那么总共有N-1个可能的候选分割阈值点,每个候选的分割阈值点的值为上述排序后的属性值中两两前后连续元素的中点;用信息增益率选择最佳划分。
处理缺失值:为属性的每个可能值赋予一个概率。例如,给定一个布尔属性Fi,如果结点t包含6个已知Fi_v=1和4个Fi_v=0的实例,那么Fi_v=1的概率是0.6,而Fi_v=0的概率是0.4。于是,实例x的60%被分配到Fi_v=1的分支,40%被分配到另一个分支。这些片断样例(fractionalexamples)的目的是计算信息增益,另外,如果有第二个缺少值的属性必须被测试,这些样例可以在后继的树分支中被进一步细分。
剪枝方法采用基于错误剪枝EBP(Error-BasedPruning)。

3. C5.0
思想:加入Boosting算法框架
二叉树不易产生数据碎片,精确度往往也会高于多叉树,所以在CART算法中,采用了二元划分。
分类目标:Gini指标、Towing、orderTowing
回归目标:最小平方残差、最小绝对残差
分类树
标记节点 t 的类:
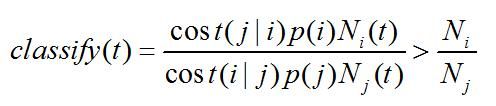
若对于除i类外的所有类j都都成立,则将N标记为类i。
其中,Pi是类i的先验概率,Ni是总数据集中类i的样本数,Ni(t)是t 的数据集中类i的样本数,cost(j | i)是误分类成本。

回归树

划分(属性)F将t划分成左右节点tL和tR,phi值:
能最大化上式的就是最佳的(属性)划分。
剪枝方法主要有
第二部分 C4.5源码分析
C4.5的源码来源于 http://www.rulequest.com/Personal/
一、数据结构
defns.i 声明一些常量,如Eof、Nil、Epsilon;函数的宏定义,如Random()、Log(x)、ForEach(v, f, l)、Verbosity(d)、Check(v, l, h)
types.i 声明一些变量,如Boolean、ItemNo(样本编号)、ItemCount(样本权重)、ClassNo(类编号)、Attribute、AttValue
*Tree,TreeRec: NodeType 0,1,2,3
Leaf 最可能的类
Items 样本数量(权重)
*Branch 子树
........
extern.i 声明外部变量
buildex.i 声明建树用的外部变量,对于build.c中的声明
ItemCount *Weight, 样本权重
**Freq, 属性值的类的频率
*ValFreq, 属性值的频率
*ClassFreq; 类值的频率
float *Gain, 各属性的增益
*Info, 各属性的内在信息
*Bar, 连续属性的最佳上界
*UnkownRate; 未知属性的比例
Boolean *Tested, 属性是否已被测试
MultiVal; 属性是否有多个值
重要声明:C4.5.c中 MaxItem(样本的最大编号)、MaxAtt、MaxClass、*Item(样本数组)、*ClassResult(分类结果数组)、*MaxAttVal(每个属性的值的个数)、*ClassName(类名数组)、*AttName(属性名数组)、**AttValName(属性值名数组)、*Pruned(剪枝树)。
besttree.c中 *Raw(未剪枝树)
二、建树逻辑
| C4.5.c | bestTree.c | build.c | discv.c | contin.c | info.c |
| GetNames()读类名、属性 | |||||
| GetData()读样本数据 | |||||
| OneTree()建一棵树/BestTree()试验多棵树取最佳 | |||||
| InitialiseTreeData() | |||||
| InitialiseWeights();初始1.0 | |||||
| Tree FormTree() | |||||
| ClassFreq=统计各类的频率 | |||||
| NoBestClass=最大频率的类 | |||||
| 计算每个属性的增益和内在信息 | |||||
| EvalDiscreteAtt() | EvalContinuousAtt() | ||||
| Freq=统计属性值的类的频率 | Quicksort() | ||||
| ValFreq=统计属性值的频率 | 找最好的SplitGain[i] | ||||
| ComputeGainComputeGain() | |||||
| TotalInfo() | |||||
| 找最好属性:Gain/Info | |||||
| 清除Unknow属性 | |||||
| 递归调用FormTree()或Leaf() | |||||
第三部分 AdaBoost算法的改造
一、AdaBoost算法
AdaBoost是一种典型的boosting算法。AdaBoost 算法的主要思想是在训练集上维护一套权重分布,初始化时,Adaboost 为训练集的每个训练例指定相同的权重 1/m。接着调用弱学习算法进行迭代学习。每次迭代后更新训练集上不同样本的权值,对训练失败的样本赋以较大的权重,也就是让学习算法在后续的学习过程中集中对比较难的训练例进行学习。
每次循环:
1)依据带权值的样本集训练基分类器G(x)
2)计算G(x)的错误率
3)计算G(x)的系数
4)更新样本集的权值分布
其中Zt是规范化因子,为所有权值之和。
经过T次循环,得到T个基分类器。
分类测试时,采用线性组合(加权投票)的方式决定最终分类:
二、使用C4.5基分类器的AdaBoost算法实现
Boosting算法对每个样本都赋予一个变化的权值,这就存在基分类器如何使用带权的样本训练的问题。有两种方式:一种是直接使用带权的样本,基分类器需要能直接使用带权样本训练;另一种是将样本权值看作其出现的概率,每次按概率重新采样,然后对采用使用基分类器训练。
C4.5分类器中,通过第二部分源码分析可知,Weight数组代表的即是样本权重。AdaBoost算法的实现中只需更新该数组即可。但该源码中对样本权重的精度支持不够,可能和Epsilon常量有关。实际作者将样本初始仍设为1.0,而不是1/m,Zt规范化因子取所有值之最大值,而非之和。