[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]
- 作者:邹祁峰
- 邮箱:[email protected]
- 博客:http://blog.csdn.net/qifengzou
- 日期:2014.03.07 18:00
- 转载请注明来自"祁峰"的CSDN博客
1 问题描述
现有两条装配线,Sij表示第i条上完成第j道工序的装配站。汽车完成组装需要依次完成1~n工序。请找出完成装配并离开装配线的最快路线。
符号说明:
①、ei:汽车进入装配线i的时间,i=1,2
②、xi:汽车离开装配线i的时间
③、aij:在装配站Sij完成装配需要的时间
④、tij:在装配站Sij完成后离开第i条装配线,进入另一条装配线需要的转移时间
注意,如果完成工序后,下一个工序还在同一条装配线上,则不需要转移时间。
图1 装配线调度
2 问题分析
3 问题求解
3.1 递归求解
递归求解的过程,可是使用如下的树形结构来表示:
图5 树形表示
3.2 动态规划
如果反过来,采用自下而上的方式来求解,把求解结果保存起来,后续的计算都依赖之前计算保存的结果,则可有效的减少重复计算,从而极大的提高求解效率。
我们再回头看看问题描述,并自下而上的方式来分析其处理过程:
第1行1列的最短耗时:ms[1][1] = e[1] + a[1][1]
第2行1列的最短耗时:ms[2][1] = e[2] + a[2][1]
第1行2列的最短耗时:ms[1][2] = min{ms[1][1], ms[2][1]+t[2][1]} + a[1][2],并记录min{ms[1][1], ms[2][1]+t[2][1]}中更小值的行号
第2行2列的最短耗时:ms[2][2] = min{ms[1][1]+t[1][1], ms[2][1]} + a[2][1],并记录min{ms[1][1]+t[1][1], ms[2][1]}中更小值的行号
第1行3列的最短耗时:ms[1][3] = min{ms[1][2], ms[2][2]+t[2][2]} + a[1][3],并记录min{ms[1][2], ms[2][2]+t[2][2]}中更小值的行号
第2行3列的最短耗时:ms[2][3] = min{ms[1][2]+t[1][2], ms[2][2]} + a[2][3],并记录min{ms[1][2]+t[1][2], ms[2][2]}中更小值的行号
....
第1行n列的最短耗时:ms[1][n] = min{ms[1][n-1], ms[2][n-1]+t[2][n-1]} + a[1][n],并记录min{ms[1][n-1], ms[2][n-1]+t[2][n-1]}中更小值的行号
第2行n列的最短耗时:ms[2][n] = min{ms[1][n-1]+t[1][n-1], ms[2][n-1]} + a[2][n],并记录min{ms[1][n-1]+t[1][n-1], ms[2][n-1]}中更小值的行号
第1行n列到终点最短耗时:ms[1][n+1] = ms[1][n] + x[1]
第2行n列到终点最短耗时:ms[2][n+1] = ms[2][n] + x[2]
此时如果想知道到达终点的最佳路径,只需比较ms[1][n+1]和ms[2][n+1]中哪个更小,并依据记录的且一列行号反推出最短路径。因整个计算过程中都将{最短耗时,前一列行号}对应的保存了起来,后续输入任何一个坐标,便能依据{最短耗时,前一列行号}找到前一列行号,根据前一行行号又能获取到对应的保存结果{最短耗时,前一列行号},通过保存结果又可以获取到更前一列行号,依次类推,便能反推出从起点到达查询点的最佳路径,而此过程不用再做任何的耗时计算。
当装配线条数为rows(rows > 2), 装配站个数为cols(cols > 1)时,其处理过程类似:
第r行c列的最短耗时:ms[r][c] = min{ms{1][c-1] + t[1][c-1], ms{2][c-1] + t[2][c-1], ..., ms{r][c-1] + t[r][c-1], ..., ms[rows][cols] + t[rows][c-1]} + a[r][c].其中的同行的转移时间t[r][c-1]=0;
图6 装配示意图
4 代码实现
4.1 结构定义
#define DYNC_LINE_NUM (2) /* 装配线条数 */ #define DYNC_NODE_NUM (6) /* 各装配线装的装配节点(装配站)数 */ #define DYNC_IN_TM_MOD (9) /* 进组装线耗时取模 */ #define DYNC_OUT_TM_MOD (9) /* 出组装线耗时取模 */ #define DYNC_NODE_TM_MOD (17) /* 各结点装线耗时取模 */ #define DYNC_TRANS_TM_MOD (9) /* 切换组装线耗时取模 */
/* 耗时类型 */
typedef enum
{
DYNC_IN_TM, /* 进组装线耗时 */
DYNC_OUT_TM, /* 出组装线耗时 */
DYNC_NODE_TM, /* 各结点装线耗时 */
DYNC_TRANS_TM, /* 切换组装线耗时 */
DYNC_TM_TYPE_TOTAL /* 耗时类型 */
}DYNC_TM_TYPE_e;
/* 最优路由信息 */
typedef struct
{
int spend; /* 当前最短花费时间 */
int lrow; /* 上一节点所在行号 */
}dync_optmz_t;
/* 耗时信息表 */
typedef struct
{
int *in; /* 进装配线耗时信息 */
int *out; /* 出装配线耗时信息 */
int *node; /* 各装配线结点耗时信息 */
int *trans; /* 切换装配线耗时信息 */
}dync_time_t;
/* 动态规划结构体 */
typedef struct
{
int rows; /* 装配线条数 */
int cols; /* 单条装配线的结点个数 */
dync_time_t time; /* 装配线各时间消耗信息 */
dync_optmz_t *optmz; /* 最佳路由结果集 */
}dynamic_t;
4.2 代码实现
/******************************************************************************
**函数名称: dync_init
**功 能: 动态规划初始化
**输入参数:
** rows: 装配线条数
** cols: 装配站个数
**输出参数:
** _dync: 动态规划对象
**返 回: VOID
**实现描述:
** 1. 为对象分配空间
** 2. 设置各操作耗时情况表
**注意事项:
**作 者: # Qifeng.zou # 2014.03.06 #
******************************************************************************/
int dync_init(dynamic_t **_dync, int rows, int cols)
{
dynamic_t *dync = NULL;
do
{
/* 1. 为对象分配空间 */
dync = (dynamic_t *)calloc(1, sizeof(dynamic_t));
if(NULL == dync)
{
break;
}
dync->time.in = (int *)calloc(rows, sizeof(int)); /* 入装配线耗时: 个数与装配线条数一致 */
if(NULL == dync->time.in)
{
break;
}
dync->time.out = (int *)calloc(rows, sizeof(int)); /* 出装配线耗时:个数与装配线条数一致 */
if(NULL == dync->time.out)
{
break;
}
dync->time.node = (int *)calloc(rows*cols, sizeof(int)); /* 装配站耗时:装配线条数*装配站个数 */
if(NULL == dync->time.node)
{
break;
}
dync->time.trans = (int *)calloc(rows*cols*rows, sizeof(int)); /* 转移耗时:装配线条数*装配站个数*装配线条数 */
if(NULL == dync->time.trans)
{
break;
}
/* 长度+1是为了存储最后一个结点至出组装线的总时间 */
dync->optmz = (dync_optmz_t *)calloc(rows*(cols + 1), sizeof(dync_optmz_t));
if(NULL == dync->optmz)
{
break;
}
/* 2. 设置各操作耗时情况表 */
dync->rows = rows;
dync->cols = cols;
set_time(dync->time.in, rows, cols, DYNC_IN_TM, DYNC_IN_TM_MOD);
set_time(dync->time.out, rows, cols, DYNC_OUT_TM, DYNC_OUT_TM_MOD);
set_time(dync->time.node, rows, cols, DYNC_NODE_TM, DYNC_NODE_TM_MOD);
set_time(dync->time.trans, rows, cols, DYNC_TRANS_TM, DYNC_TRANS_TM_MOD);
*_dync = dync;
return 0;
}while(0);
/* 异常处理: 释放所有内存 */
if(NULL != dync)
{
if(NULL != dync->time.in) { free(dync->time.in); }
if(NULL != dync->time.out) { free(dync->time.out); }
if(NULL != dync->time.node) { free(dync->time.node); }
if(NULL != dync->time.trans) { free(dync->time.trans); }
if(NULL != dync->optmz) { free(dync->optmz); }
free(dync), dync=NULL;
}
return -1;
}
为了方便快速设置耗时信息,在此使用函数自动处理:
/******************************************************************************
**函数名称: set_time
**功 能: 设置耗时信息
**输入参数:
** rows: 装配线条数
** cols: 装配站个数
** type: 耗时类型
** mod : 耗时取模
**输出参数:
** node: 各装配站耗时
**返 回: VOID
**实现描述:
**注意事项:
**作 者: # Qifeng.zou # 2014.03.06 #
******************************************************************************/
void set_time(int *tm, int rows, int cols, int type, int mod)
{
int row = 0, row2 = 0, col = 0, base = 0;
switch(type)
{
case DYNC_IN_TM:
case DYNC_OUT_TM:
{
printf("\nIN/OUT TIME:\n");
for(row=0; row<rows; row++)
{
tm[row] = 0;
while(0 == tm[row])
{
tm[row] = random()%mod;
}
printf("[%03d] ", tm[row]);
}
printf("\n\n");
break;
}
case DYNC_NODE_TM:
{
printf("\nNODE TIME:\n");
for(row=0; row<rows; row++)
{
printf("[ROW:%02d]\n", row);
for(col=0; col<cols; col++)
{
while(0 == tm[row*cols + col])
{
tm[row*cols + col] = random()%mod;
}
printf("[%03d] ", tm[row*cols + col]);
}
printf("\n");
}
printf("\n");
break;
}
case DYNC_TRANS_TM:
{
printf("\nTRANS TIME:\n");
for(row=0; row<rows; row++)
{
printf("[ROW:%02d]\n", row);
for(col=0; col<cols; col++)
{
base = row*cols*rows + col*rows;
printf("COL:[%03d]-", col);
for(row2=0; row2<rows; row2++)
{
tm[base + row2] = 0;
while((0 == tm[base + row2]) && (row != row2))
{
tm[base + row2] = random()%mod;
}
printf("[%03d] ", tm[base + row2]);
}
printf("\n");
}
printf("\n");
}
break;
}
}
}
/******************************************************************************
**函数名称: dync_proc
**功 能: 动态规划: 计算最短路径并存储
**输入参数:
** dync: 动态规划对象
**输出参数:
**返 回: VOID
**实现描述:
**注意事项:
**作 者: # Qifeng.zou # 2014.03.06 #
******************************************************************************/
void dync_proc(dynamic_t *dync)
{
int *spend = NULL;
dync_optmz_t *best = dync->optmz, *curr = NULL, **line = NULL, *prev = NULL;
int curr_row = 0, row = 0, col = 0, min_spend = 0, min_row = 0;
spend = (int *)calloc(dync->rows, sizeof(int));
if(NULL == spend)
{
return;
}
line = (dync_optmz_t **)calloc(dync->rows, sizeof(dync_optmz_t*));
if(NULL == line)
{
free(spend);
return;
}
/* 逐列遍历 */
for(col=0; col<dync->cols; col++)
{
memset(spend, 0, dync->rows * sizeof(int));
if(col > 0)
{
/* 指向各行前一列 */
for(row=0; row<dync->rows; row++)
{
line[row] = &best[row*(dync->cols+1) + col - 1];
}
}
/* 逐行当前列遍历 */
for(curr_row=0; curr_row<dync->rows; curr_row++)
{
curr = &best[curr_row*dync->cols + col];
if(0 == col)
{
curr->spend = (dync->time.node[curr_row*dync->cols + col] + dync->time.in[curr_row]);
curr->lrow = -1;
continue;
}
/* 统计逐行前列至当前站点耗时 */
for(row=0; row<dync->rows; row++)
{
spend[row] = (line[row]->spend
+ dync->time.node[curr_row * dync->cols + col]
+ dync->time.trans[row * dync->cols * dync->rows + (col - 1) * dync->rows + curr_row]);
}
/* 查找最小耗时路径 */
min_spend = spend[0];
min_row = 0;
for(row=1; row<dync->rows; row++)
{
if(min_spend > spend[row])
{
min_spend = spend[row];
min_row= row;
}
}
curr->spend = min_spend;
curr->lrow = min_row;
}
}
/* 计算装配线最后一节点至出站耗时 */
for(row=0; row<dync->rows; row++)
{
prev = &best[row*(dync->cols+1) + dync->cols - 1];
curr = &best[row*(dync->cols+1) + dync->cols];
curr->spend = (prev->spend + dync->time.out[row]);
curr->lrow = row;
}
/* 内存释放 */
free(spend), spend=NULL;
free(line), line=NULL;
return;
}
/******************************************************************************
**函数名称: dync_show
**功 能: 搜索并显示最佳路径
**输入参数:
** dync: 对象
** row: 行号
** col: 列号
**输出参数:
**返 回: VOID
**实现描述:
**注意事项:
**作 者: # Qifeng.zou # 2014.03.06 #
******************************************************************************/
void dync_show(const dynamic_t *dync, int row, int col)
{
const dync_optmz_t *optmz = NULL, *prev = NULL;
if(row >= dync->rows)
{
row = dync->rows - 1;
}
if(col > dync->cols)
{
col = dync->cols;
}
fprintf(stdout, "\n");
optmz = &dync->optmz[row*(dync->cols+1) + col];
fprintf(stdout, "[%d][%d] Total: %d\n", row, col, optmz->spend);
while(col >= 0)
{
if(-1 == optmz->lrow)
{
fprintf(stdout, "[%02d][%02d]: CURR:%03d [PREV:L%02d-IN:%03d] | TOTAL:%03d\n",
row, col,
dync->time.node[row * dync->cols + col],
optmz->lrow,
dync->time.in[row],
optmz->spend);
break;
}
else if(dync->cols == col)
{
prev = &dync->optmz[optmz->lrow*(dync->cols+1) + (col-1)];
fprintf(stdout, "[%02d][%02d]: OUT:%03d [PREV:L%02d-SPEND:%03d] | TOTAL:%03d\n",
row, col,
dync->time.out[row],
optmz->lrow, prev->spend,
optmz->spend);
}
else
{
prev = &dync->optmz[optmz->lrow*(dync->cols+1) + (col-1)];
fprintf(stdout, "[%02d][%02d]: CURR:%03d [PREV:L%02d-SPEND:%03d-TRANS:%03d] | TOTAL:%03d\n",
row, col,
dync->time.node[row * dync->cols + col],
optmz->lrow, prev->spend,
dync->time.trans[optmz->lrow * dync->cols * dync->rows
+ (col - 1) * dync->rows + row],
optmz->spend);
}
col--;
row = optmz->lrow;
optmz = &dync->optmz[optmz->lrow*(dync->cols+1) + col];
}
return;
}
代码6 显示路径
函数调用示例:
int main(int argc, const char *argv[])
{
dynamic_t *dync = NULL;
int ret = 0, row = 0, col = 0;
if(3 != argc)
{
fprintf(stderr, "Please input arguments!\ndynamic 2 3\n");
return -1;
}
row = atoi(argv[1]);
col = atoi(argv[2]);
ret = dync_init(&dync, DYNC_LINE_NUM, DYNC_NODE_NUM);
if(0 != ret)
{
fprintf(stderr, "Initialize dync_proc failed!\n");
return -1;
}
dync_proc(dync);
dync_show(dync, row, col);
return 0;
}
4.3 结果展示
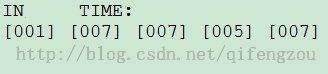
假设有5条装配线,每条装配线上有9个装配站,则有如下数据:①、入装配线的耗时分别为:
②、出装配线的耗时分别为:
图8 出装配线耗时
③、各装配线的装配站耗时分别为:
图9 各装配站耗时
④、各装配站切换装配线耗时分别为:
图10 切换装配线耗时
⑤、查找最佳路径
输入(4,8)的最佳路径是:起点->L01->L04->L01->L03->L03->L03->L03->L02->(4, 8)
图11 最佳路径
图12 路径绘制
![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第1张图片](http://img.e-com-net.com/image/info5/e7dcd94d7eaa4f0d90b2dd9bf152e113.jpg)

![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第2张图片](http://img.e-com-net.com/image/info5/201888184c704fa5986d56e5a8cec533.jpg)
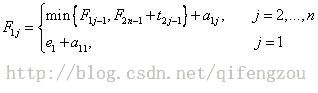
![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第3张图片](http://img.e-com-net.com/image/info5/dd28157cb9bd42fbb2ca9f16bfd8e2fd.jpg)
![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第4张图片](http://img.e-com-net.com/image/info5/f47972fc457c44639b622e27c7fffa4a.jpg)

![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第5张图片](http://img.e-com-net.com/image/info5/bc8922059ad64a72b4d70c2d96d8d61f.jpg)
![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第6张图片](http://img.e-com-net.com/image/info5/95ab260d9b00421694c77571f3ff0e1a.jpg)
![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第7张图片](http://img.e-com-net.com/image/info5/3c731cc4481043c3bbe0d4ada1f0a350.jpg)
![[置顶] 算法导论 之 动态规划 - 装配线调度问题[C语言]_第8张图片](http://img.e-com-net.com/image/info5/ae0cb01531c24917aff1c3c77e437988.jpg)