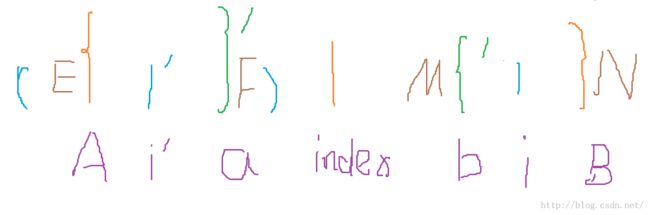牛客堂刷题之Manacher算法

题目：

给定一个字符串str，返回str中的最长回文子串的长度。

str=“123”。其中的最长回文子串“1”或者“2”或者“3”，所以返回1。

str=“abc1234321ab”。其中的最长回文子串“1234321”，所以返回7。

思路：

可以首先想到的办法就是，遍历数组，然后往每个元素的两边扩充，然后扩充的最长的就是最长回文子串。

但是扩充的复杂度加上遍历数组的复杂度，整个算法的复杂度就是O(n^2)

但是相对于奇数和偶数，此方法还需要区分。因为1221，利用上面方法就无法判断此序列有回文串，因为最中间是一个虚轴。

基于这个，我们首先给每个数字之间加上一个别的数，#1#2#2#1#，这样既可以实现偶数和奇数一样的处理方法。最终的回文串长度除以2就是原串的长度。

我们首先需要定义三个变量：

pArr[]数组，存储每个元素的回文半径：#a#b#c#，那么pArr[3]=4。

pR，以i为中心，最远扩到距离的下一个元素，#a#b#c#，i等于3时，pR就等于7

index，回文半径的中心，例如上面的index就为3，当更新pR的时候，就更新index。

我们需要做的优化就是用已处理的优化未处理的，那么有四种拓扑

第一种情况：

 

情况是：我们遍历到i位置时，需要求取以i为中心的回文半径，即i位置能扩多远。

此时，index处于如图所示的点，以index为中心的回文序列边界是A~~~B，此时我们需要求取i位置的回文半径，那么 i 位置相对于index对称的就是 i' 位置，我们之前已经得到 i' 位置的回文半径存储在pArr数组中，边界假设为a~~~b，又因为A~~~B是以index为中心的回文序列，那么a'~~~~b' 就是a~~~b的逆序（a'和b'是a、b关于index对称的镜像），那么a'~~b'就也是回文的，那么 i 的回文半径也就是a'~~~b'

例如：#d#a#b#c#f#c#b#a#e#，那么第2个b的回文半径就是第一个b的回文半径

第二种情况：

同上例，以index为中心的A~~~B为回文边界，我们此时需要求取 i 的回文半径，那么 i' 就是 i 关于index对称的镜像，可是此时 i' 的回文半径已经出了A~~~B，所以无法衡量。

我们假设A关于 i‘ 的镜像是a，A左边的元素是E，a右边的元素是F，我们可以得到E==F，同理，b为B关于 i 的镜像，但是无法确定M是否等于N，我们知道整体是一个大的回文序列，那么a~~~b就是一段小的回文序列，所以F==M，并且A~~~B是边界，我们可以确定的是 E!=N。所以我们得出E==F==M，E!=N，所以M!=N。所以i的回文序列是b~~~B

例如：#a   #b#a#c#a#b#  d#，右b为i，他的镜像已经超出了c的回文边界，所以右b的回文边界是{c的右边界关于b的镜像，c的右边界}

第三种情况：

同例，此时 i 的镜像 i' 的回文左边界恰好和index的回文左边界重合，那么我们只能得出 i 的回文边界是从N~~~B开始（N为M关于index的镜像），然后我们可以继续往后扩即可

例子：#d    #a#b#a#  c#a#b#a#     c# ，可以看出c的回文序列是abacaba，但是右b的回文序列就比左b的回文序列长，所以还要继续扩

第四种情况：

这种情况就是当 i 大于pR的时候，i的半径默认是1，从1开始扩，因为两个本来就没重合，所以没法优化

代码

	public static char[] manacherString(String str)
	{
		
		//将abc变为#a#b#c#
		char [] oldStr = str.toCharArray();
		char [] newStr = new char[str.length()*2+1];
		
		int index=0;
		for(int i=0;i<newStr.length;i++)
		{
			newStr[i] =( (i&1)==0?'#':oldStr[index++]);
		}
		return newStr;
	}
	
	public static int getManacherString(String str)
	{
		if(str==null||str.length()==0)
			return -1;
		char [] newStr =  manacherString(str);
		 
		 
		int[] pArr = new int[newStr.length+1];
		int pR=-1;
		int index=-1;
		int max=Integer.MIN_VALUE;
	 
		
		for(int i=0;i<newStr.length;i++)
		{
			
			//pR-i就是为了防止镜像i超出总边界
		       pArr[i] = pR > i ? Math.min(pArr[2 * index - i], pR - i) : 1;//左老师的这句代码实在经典
			  
			while(i+pArr[i]<newStr.length && (i-pArr[i]) >=0) //开始扩，从指定位置，或者从1
			{
				if(newStr[i+pArr[i]]==newStr[i-pArr[i]])
					pArr[i]++;
				else 
					break;
			}	
			//若pR更右，则替换
			if(i+pArr[i]>pR)
			{
				pR=i+pArr[i];
				index=i;
			}
			 
			max = Math.max(max, pArr[i]);
		}
  
		return max-1;
	}

题目进阶

 给定一个字符串str，想通过添加字符的方式使得str整体都变成回文字符串，但要求只能在str的末尾添加字符，请返回在str后面添加的最短字符串。

str=“12”。在末尾添加“1”之后，str变为“121”是回文串。在末尾添加“21”之后，str变为“1221”也是回文串。但“1”是所有添加方案中最短的，所以返回“1”。 

思路

利用Manacher算法我们可以得到每个元素的回文半径，那么当我们得到某一元素的回文半径已经达到序列的最右侧，我们只需要将左侧没包含的逆序增加进来即可

例如：12343，当index为4时，那么回文半径已经达到最右端（PR指向最右边），那么我们只需要将12，逆序增加到尾部即可。

因为牵扯到奇偶数，所以还需要处理原字符串

代码：

public static char[] manacher(String str)
	{
		//处理原字符串
		char [] ss = str.toCharArray(); 
		char[] newStr = new char[str.length()*2+1];
		int index=0;
		for(int i=0;i<newStr.length;i++)
		{
			newStr[i] = (i&1)==0?'#':ss[index++];
		}
		return newStr;
	}
	
	public static void getManacher(String str)
	{
		
		if(str==null || str.length()==0)
			return;
		char []newStr = manacher(str);
		int index=-1;
		int pR=-1;
		int[] pArr = new int[newStr.length];
		int end =-1;
		for(int i=0;i<newStr.length;i++)
		{
			pArr[i] = pR<=i? 1 :Math.min(pR-i, pArr[2*index-i]);
			
			while(pArr[i]+i<newStr.length && i-pArr[i]>=0)
			{
				if(newStr[pArr[i]+i]==newStr[i-pArr[i]])
					pArr[i]++;
				else
					break;
			}
			if(i+pArr[i]>pR)
			{
				index = i;
				pR = i+pArr[i];
			}
			//回文边界到达最右侧时，即pR到达最右侧
			if(pR==newStr.length)
			{
				end=pArr[i];
				break;
			}
			
		}
		char[] res=new char[str.length()-(end-1)];//总长度，减去回文串长度
		for(int i=0;i<res.length;i++)
		{
			res[res.length-1-i] = newStr[2*i+1];
		}
		
		System.out.println(str);//原字符串
		System.out.println(new String(res));//需要添加的字符串
	}