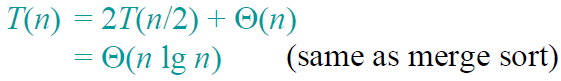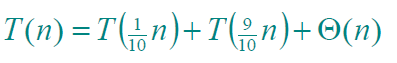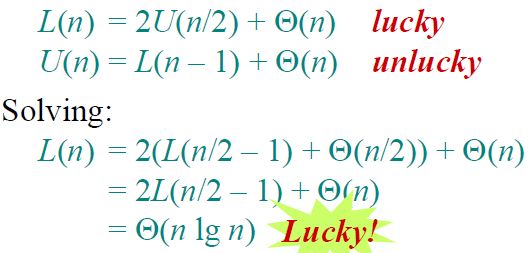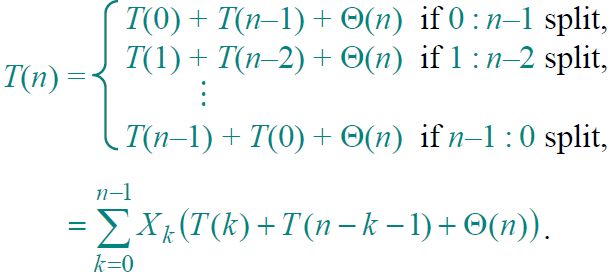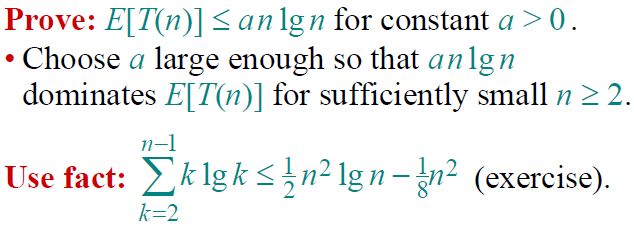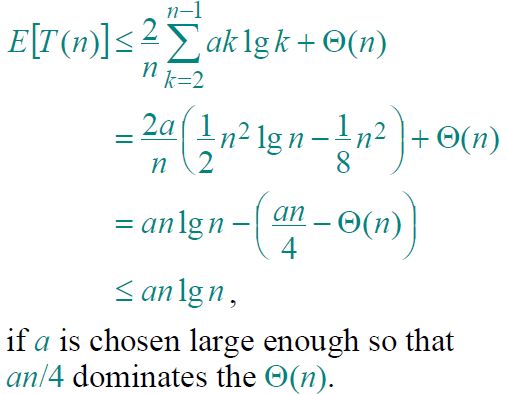MIT算法导论——第四讲.Quicksort
本栏目(Algorithms)下MIT算法导论专题是个人对网易公开课MIT算法导论的学习心得与笔记。所有内容均来自MIT公开课Introduction to Algorithms中Charles E. Leiserson和Erik Demaine老师的讲解。(http://v.163.com/special/opencourse/algorithms.html)
第四节-------快速排序 Quicksort
这节课的主要内容分为两部分,一部分是介绍快速排序算法,分析其在最好、最坏以及最好最差交替出现情况下的算法效率;另一部分则是介绍随机化快排算法,以及分析其算法复杂度。后者也是视频中最精彩的部分。
一、快速排序
快速排序由Tony Hoare在1962年提出,是基于分治思想(Divide-and-conquer)的一种原地排序,但其效率依赖于输入数据的排序状况。所谓原地排序,即指算法的空间复杂度为O(1),它就在原来的数据区域内进行重排。就像插入排序一样,就在原地完成排序。但是归并排序就不一样,它则需要额外的空间来进行归并排序操作。
如下图所示是快速排序中的分治法思想。
由上图可以知道,快速排序里面最关键的就是第一步:分化(Partition)的步骤,这是该算法处理问题的核心。所以我们可以把快排看成是递归地划分数组,就想归并排序是递归地合并数组一样。关于Paritition的具体算法,目前有好几种,其伪代码稍有不同但是它们的原理都是一样的。当然最重要的一点是它们的算法复杂度都是线性的,也就是O(n)。下面是快排的递归伪代码。
当然上面只是一个核心的递归代码。一个让快排运行更快的方法时调整这里的代码,找到适合元素数目较少的特别的算法。比如说,只剩下5个元素,你已经知道了一些代码来高效地排序5个元素,那么用那个特别的算法来替代这里的递归就会好一些。还有一些其他的办法,譬如说这是尾递归的代码,那么就可以使用一些尾递归的优化等等。。。
接下来分析快排的算法效率,在分析中假设所有的元素都是不同的。当重复元素存在时,这里的代码运行的就不是很好,但是Hoare最初的分划方法在待排序的元素中有重复的情况下更为高效。有时间的时候去看一下那个方法,它使用一个更加复杂的不变量来实现分划过程,但是本质上是一样的。
1、最坏情况下分析
那怎样的情况算是快速排序的最坏情况呢?当然是当输入序列是正序或者是反序的时候,因为这时候分划总是围绕着最大的或者是最小的元素进行,那么造成的现象就是分划的另外一边总是没有元素,这样就无法利用递归来提高算法运算的效率。
那么,在这种情况下,快排的算法效率递归式如下图所示,易知这时的效率是Θ(n^2)。
2、最优情况下分析
我们当然没有办法保证输入序列能够满足快排的最优情况,但是我们可以这样直观地来理解:如果我们足够幸运,Partition每次分划的时候正好将数组划分成了两个相等的子数组。那么这种情况下的递归分析式如下图所示。
这显然是我们想要的结果。那么当Partition的时候达不到均等地划分,如果两个子数列划分的比例是1:9呢?
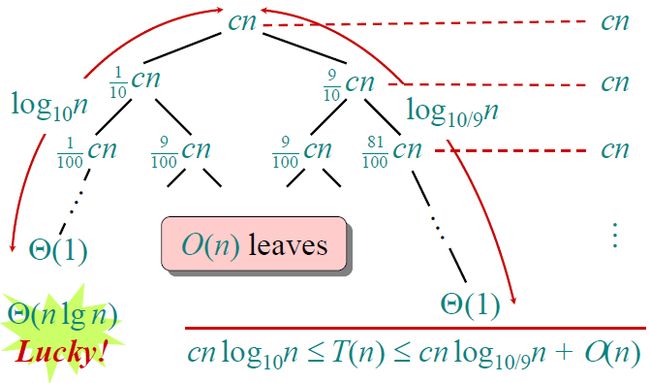
为了解这个递归式,主方法是派不上用场了。这时候搬出总是能够有效的分析树,如下图所示。
综上所述,可以知道快排在最优情况下的算法效率是Θ(nlgn)。
3、最坏与最优交替出现情况下分析
上面我们分析了最好与最坏情况下的算法效率,那么更加普遍的情况是,当最坏情况与最优情况同时都有出现时的算法效率呢?我们假设算法中最坏与最优情况交替出现,那么算法的效率分析如下图所示。
可以得知,在这样的情况下我们也还是幸运的,得到的算法效率与最优情况下的效率一样。那么我们如何保证我们总是幸运的呢?这也是随机化快速排序需要解决的问题。
二、随机化快速排序
我们已经知道,若输入本身已被排序,那么对于快排来说就糟了。那么如何避免这样的情况?一种方法时随机排列序列中的元素;另一种方法时随机地选择主元(pivot)。这便是随机化快速排序的思想,这种快排的好处是:其运行时间不依赖于输入序列的顺序。也就是说我们不再需要对输入序列的分布作任何假设,没有任何一种特定的输入序列能够使算法的效率极低。最不幸运的情况有可能会发生,但是也是因为随机数产生器的原因,不是因为输入序列的原因。
这里的办法是随机地选择主元。如下图所示是随机化快速排序的算法效率递归表达式。
其中,X(k)是一个指示器随机变量,用来简化上述递归式中的复杂度。
因此,计算随机化算法的算法效率就演变成了计算上述含有指示器随机变量的递归式的期望值,具体过程如下图所示。
得到如上图所示的递归式后,如何求解成了一个问题。这里用的方法是替换法(Substitution method)。
这样,就得到了随机化快排的算法效率是Θ(nlgn)。
在实践中,快速排序是一个很好的算法。它虽然不能保证归并排序所提供的在最坏情况下nlgn的运行时间,但是在实践中如果采用随机化快速排序算法,通常比归并排序快3倍以上。当然不可否认的是,确实需要一些编码技巧来使它打到那样的速度,你需要优化基础情况以及其他的一些技巧,但是大部分好的算法都是基于快速排序的。
快速排序很好的另一个原因是它在虚拟内存的缓存中性能比较好。
关于Introduction to Algorithms更多的学习资料将继续更新,敬请关注本博客和新浪微博Sheridan。