root locus 根轨迹 自动控制原理

root locus

定义：

        单位负反馈系统的开环传递函数特征方程常数项从0增大到无穷大过程中，根的变化

例如：

        开环传递函数G(s) = K/(s*(s+2))

特征方程就是闭环传递函数分母多项式等于0的方程！

特征方程为s^2+2*s+K = 0; K 从0 增大到无穷大的过程中，特征方程根的变化轨迹就是根轨迹

“定义” 嗯?定义了有什么用？为什么是这样的？根轨迹用来干嘛的？

           感觉中国教育很多时候就是一笔带过，能敷衍的就敷衍，很多时候没有切实深刻的追究问题的来源，是这样就这样了。。。。。慢慢的就不求甚解，自我感觉良好的时候，其实都是浮躁作怪

回答为什么会有根轨迹！

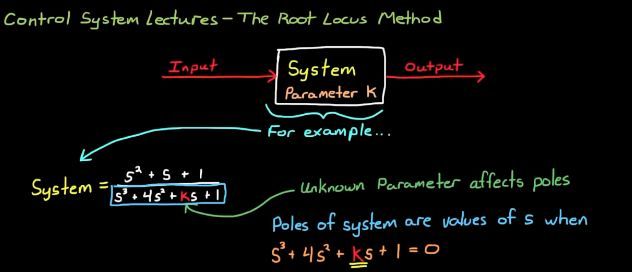
             如上图，一个系统的传递函数知道了system，如果其中有一项的系数不知道，未知，这可能是系统正在调试，要确定这个参数为什么值的时候，系统输出表现的好而出现的参数待定情况

            系统的极点就是分母为0的时候，对应的根，即为极点。K值是对极点有影响的，它是特征方程的系数，是决定极点位置的。

                     根轨迹就是研究当这个未知系数K变化的时候，系统极点变化的情况，把K从0变化到无穷大的过程中，根的连续变化情况在复平面内连线，形成的曲线轨迹，就是根轨迹，root locus

可以看出，就是一个个的尝试K的值，对根带来的影响

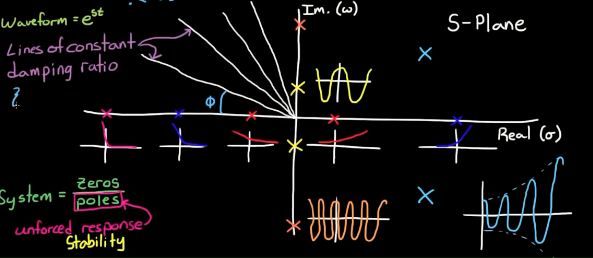
               这里过原点斜率一定的直线，小小的纠结了一会儿，在这一直线上的随着原理原点，系统的衰减率越来越大(实轴部分)，系统的震荡频率越来越大(虚轴部分)。看似没有什么联系，其实是有联系的，系统的超调，稳定时间都和阻尼有关系，阻尼是系统本身固有属性(切记！)。

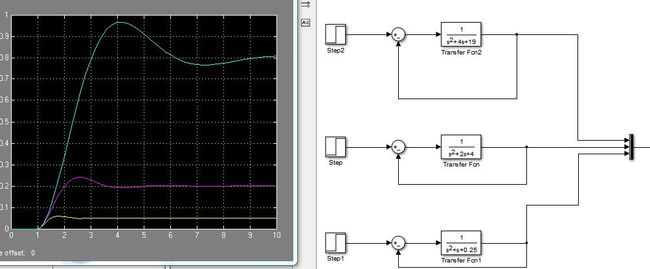
做了一个小demo

看到这幅图的时候，别的啥都别干，第一，冷静！

阻尼是反应系统本身对于震荡的反应。是系统的够有属性，我选了相同阻尼的系统都在最上面系统的极点是（-2，j4），中间的是（-1，2j），最下面的是（-0.5，1*j）

可以看出，我选的都是在斜率-0.5直线上的点

冷静的看图! 三个图像是“很相似”的，他们的超调和为超调部分的波形都是相似的！这就是阻尼！阻尼是系统本身的固有属性，描述的是超调情况

Got it ？

有时候，我们需要很好的控制系统超调的情况，传说中最好的阻尼系数(工业中也是采用最多的)——0.7

所以，我们在设计系统的时候就要考虑阻尼，而阻尼一定在复平面内表现为过原点斜率一定

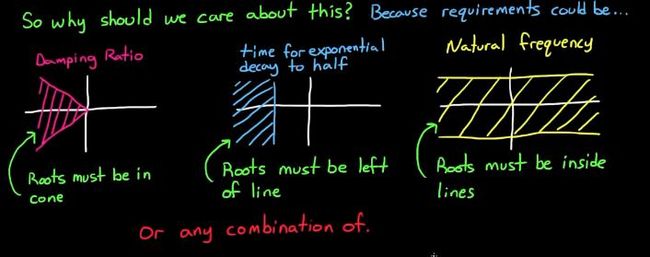
一个系统你不想要他超调到你不能忍受，对吧？考虑合适的阻尼

一个系统你不想要他稳定的极其的慢，慢到你难以忍受，对吧？考虑合适的极点实部

一个系统你不想要他震荡的过于频繁，有木有？考虑合适的极点虚部

于是设计中考虑的阻尼，极点范围，震荡频率范围(如下图说明),统统都是要考虑的因素，

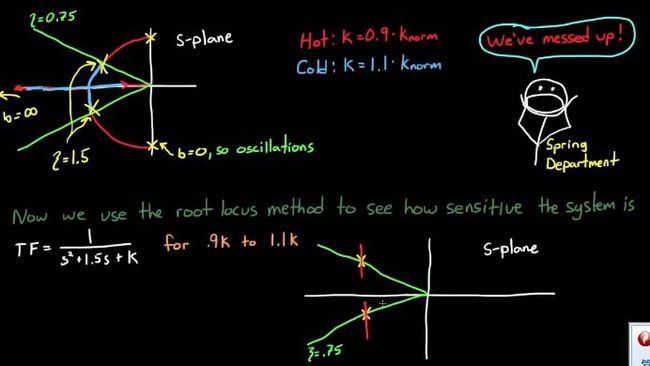
此时假设我们的系统传递函数模型是1/(s^2+bs+1)不知道b是多少，要确定它，根轨迹！上吧！

               选取好阻尼范围内的极点即可，算出系数b。 题外话，由于可能K有一定的波动，那么选取系数的时候适当的不要选阻尼线上或很临近的点，不然系统将达不到设计要求。为了满足系统一定的抗干扰能力，这时候选取离阻尼边界线有一定距离的点较佳

用matlab画根轨迹——利用rlocus函数

假设当前传递函数是G(s) = (s+1)/(s^2+s+1);

numerator = [ 1 1];%分子的系数
denominator = [1 1 1];%分母各项的系数
rlocus(numerator,denominator);

简单方便。。。。。用手画就坑爹多了。。。考试无奈。。。。