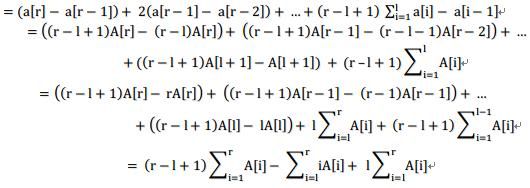关于线段树的区间修改与区间询问问题

有一类问题，它们的大意都是维护一段序列，给出两种操作，一种是对一段区间进行整体修改，一类是对一段区间询问其中元素的极值或者和。

这一类问题通常是使用线段树来解的，然而，如果操作比较简单，线段树的实现也会有不同的方法，这里以最简单的一道题poj 3468为例。

第一种方法：线段树 + lazy标记

我们使用lazy标记维护当前节点的子区间是否有延后更新，我们知道如果对于每一次的区间修改都暴力做的话复杂度是O(n)的，我们想要把它减少到O(logn),于是对于一整段区间都需要修改的情况，我们可以就在这整段区间的代表节点记下这个区间需要改变的值，当我们需要深入这个区间时再将这个信息下放下取，运用这个思想就降低了大量的冗余操作，问题就顺利解决了。

source：

#include <stdio.h>
const int nmax = 100000, tmax = 1 << 18;

long long segflag[tmax + 18], segsum[tmax + 18];
int n, q, M = 1, l, r, H = 1;
char c;
long long k;

void pushdown(int i)
{
    for (int k = H - 1, p = i >> k; k; --k, p = i >> k)
	if (segflag[p])
	{
	    segflag[p << 1] += segflag[p];
	    segflag[p << 1 | 1] +=segflag[p];
	    segsum[p] += segflag[p] * (1 << k);
	    segflag[p] = 0;
	}
}	    
	    
void add(int l, int r, long long c)
{
    l += M - 1, r += M + 1;
    long long ldel = 0, rdel = 0, sze = 1, tmp;
    for (; l ^ r ^ 1; l >>= 1, r >>= 1, sze <<= 1)
    {
	if (~l & 1) 
	{
	    segflag[l ^ 1] += c;
	    tmp = c * sze;
	    segsum[l ^ 1] += tmp;
	    ldel += tmp;
	}   
	if ( r & 1) segflag[r ^ 1] += c;
	segsum[l << 1] += ldel;
	segsum[r << 1] += rdel;
    }
}

long long getsum(int l, int r)
{
    l += M - 1;
    r += M + 1;
    pushdown(l);
    pushdown(r);
    long long cnt = 0;
    for (; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
	if (~l & 1) cnt += segsum[l ^ 1];
	if ( r & 1) cnt += segsum[r ^ 1];
    }
    return cnt;
}

int main()
{
    scanf("%d%d", &n, &q);
    while (M <= n) M <<= 1, ++H;
    for (int i = 1; i <= n; ++i)
	scanf("%I64d", segsum + i + M);
    scanf("\n");
    for (int i = M - 1; i; --i)
	segsum[i] = segsum[i << 1] + segsum[i << 1 | 1];
    for (int i = 1; i <= q; ++i, scanf("\n"))
    {
	scanf("%c %d %d", &c, &l, &r);
	if (c == 'Q')
	    printf("%I64d\n", getsum(l, r));
	else
	    scanf("%I64d", &k), add(l, r, k);
    }
    return 0;
}

	

　　

 

第二种方法：线段树 + 差分思想

这种方法，相较于前面一种，编程复杂度更小，但是思维复杂度相对较大，下面要经过一些数学推理：

假设我们需要维护的原序列为a₁, a₂…. a_n,再设一个新数组A₁, A₂ …. A_n，我们对于这个数组的定义为：

                                     A[i] = a[i] – a[I – 1] (a[0] = 0)

我们再设这两个数组的前缀和数组分别为sa₁, sa₂ …. sa_n, sA₁, sA₂, …. sA_n，即：

                                               sa[i] = sigma(j from 1 to i)a[j]

                                               sA[i] = sigma(j from 1 to i)A[j] = a[i]

那么易得：              sa[i] = sigma(j form 1 to i)a[j] = sigma(j from 1 to i)sA[j]

于是我们可知：原数组a的前缀和就是差分后的数组A的前缀和的前缀和。

现在让我们看看进行区间修改之后原数组和其差分数组的变化，假设我们将原数组[l, r]这段区间整体加上一个值k，那么

a数组： a[1],a[2]….a[l], a[l + 1]….a[r – 1], a[r]….a[n]

变成：a[1],a[2]….a[l] + k, a[l + 1] + k,….a[r – 1] + k, a[r] + k,….a[n]

 

A数组：A[1], A[2],….A[l], A[l + 1],….A[r – 1], A[r],….A[n]

变成：A[1], A[2],….A[l] + k, A[l + 1],…. A[r – 1], A[r],A[r + 1] - k,….A[n]

 

是否发现了什么？ 对区间进行修改，原数组有O(n)级别的位置的修改，而其差分数组只有两个数发生了变化！

这就是我们要使用的性质。

现在我们希望利用这个性质快速维护区间信息：

我们需要求

 

于是，只要我们能够快速统计A[i]和iA[i]的区间信息，就能够快速统计区间和，又因为对于A数组我们只需要改动两个点，所以将一个线段树支持区间修改区间查询的问题转换成了两个线段树支持单点修改区间查询的问题。

以3468的样例为例

原数组    a: 1 2 3 4 5 6 7 8 9 10

差分数组  A：1 1 1 1 1 1 1 1 1 1

辅助数组iA[i]：1 2 3 4 5 6 7 8 9 10

Q：4 4  ans：(4 + 1 - 4) * (1 + 1 + 1 + 1) – (4) + 4 * 1= 4

Q：1 10  ans：(10 – 1 + 1) * 10 – 55 + 10 = 55

Q：2 4   ans：(4 – 2 + 1) * 4 – 9 + 2 * 3 = 9

C：3 6 3  A：1 1 4 1 1 1 -2 1 1 1      iA[i]：1 2 12 4 5 6 -14 1 1 1

Q：2 4   ans：(4 – 2 + 1) * 7 – 18 + 2 * 6 = 15

问题解决。

source：

#include <stdio.h>
typedef long long ll;
const int nmax = 100000, tmax = 1 << 18;

int n, q;
ll seg[2][tmax + 18];
int a[nmax + 18];
int M = 1;
int l, r, k;
char c;

void inc(int pos, int k)
{
    int i = pos + M;
    seg[0][i] += k;
    seg[1][i] += k * pos;
    for (i >>= 1; i; i >>= 1)
	seg[0][i] = seg[0][i << 1] + seg[0][i << 1 | 1], seg[1][i] = seg[1][i << 1] + seg[1][i << 1 | 1];
}

ll getsum(ll *a, int l, int r)
{
    ll rnt = 0;
    for (l += M - 1, r += M + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
	if (~l & 1) rnt += a[l ^ 1];
	if ( r & 1) rnt += a[r ^ 1];
    }
    return rnt;
}

int main()
{
    scanf("%d%d", &n, &q);
    while (M <= n) M <<= 1;
    for (int i = 1; i <= n; ++i)
	scanf("%d", a + i), seg[0][M + i] = a[i] - a[i - 1], seg[1][M + i] = (ll)i * (a[i] - a[i - 1]);
    for (int i = M - 1; i; --i) 
	seg[0][i] = seg[0][i << 1] + seg[0][i << 1 | 1], seg[1][i] = seg[1][i << 1] + seg[1][i << 1 | 1];
    while (q--)
    {
	scanf("\n%c%d%d", &c, &l, &r);
	if (c == 'C')
	{
	    scanf("%d", &k);
	    inc(l, k);
	    if (r < n) inc(r + 1, -k);
	}
	else
	    printf("%I64d\n", getsum(seg[0], 1, r) * (r + 1 - l) - getsum(seg[1], l, r) + getsum(seg[0], l, r) * l);
    }
    return 0;
}