NYOJ 536 开心的mdd(区间DP)
题目链接:Click here~~
月赛一道dp的题,看了看解题报告,懂了些。
题意:
求n个给定顺序的矩阵连乘所要的最少乘法次数。
解题思路:
首先我们通过观察题目中举出的例子不难发现,两个矩阵(比如(m*n) * (n*o))相乘所需要的乘法次数为:m*n*o。
由于矩阵相乘是有规律的:前面的矩阵的列数等于后面的矩阵的行数。
所以我们可以用一个一维数组p[n+1]巧妙将矩阵的行数与列数记录下来。
即用p[i-1]和p[i]记录第i个矩阵的行和列,那么第i+1个矩阵的行和列为p[i]和p[i+1],也不会发生冲突。
开一个二维数组dp[n][n]。令dp[i][j]表示从第i个矩阵到第j个矩阵相乘所需要的最少乘法次数。
当i=j时,显然dp[i][j]=0。
状态转移方程为:dp[i][j] = min{dp[i][k] + dp[k+1][j] + p[i-1]*p[k]*p[j]}。(i<=k<j)
因为对于任意一组i,j,最后都可以把它分成两个矩阵相乘的形式。
对于上面这个方程来说,即把它分成了从第i到第k个相乘完得到的矩阵A与从第k+1到第j个相乘完得到的矩阵B再次相乘。
即(Ai*Ai+1*…Ak)*(Ak+1*Ak+2*…Aj)。而矩阵A的行列分别为p[i-1],p[k];矩阵B的行列分别为p[k],p[j]。
最后求得的dp[1][n]即为结果。
状态转移方程出来了,计算顺序是关键。
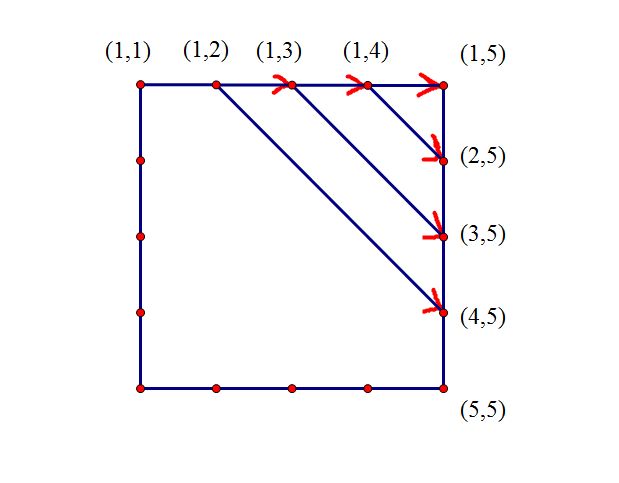
观察这个转移方程,我们不难发现要计算dp[i][j]的时候,必须要知道dp[i][k]即左边,还有dp[k+1][j]即下边。
所以,我们应该先求左下边的值。即每条45度的对角线,如下图:
代码如下:
#include <stdio.h>
#include <string.h>
int min(int a,int b)
{
return a==0 ? b : (a < b ? a : b);
}
int main()
{
int n,p[102],dp[102][102];
while(~scanf("%d",&n))
{
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++) //第i的矩阵的行号和列号分别是p[i-1],p[i]
scanf("%d%d",&p[i-1],&p[i]);
for(int d=1;d<n;d++) //控制对角线
for(int i=1;i<=n-d;i++) //控制行
{
int j = i+d; //控制列
for(int k=i;k<j;k++) //根据状态转移式求出dp[i][j]
dp[i][j] = min(dp[i][j],dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j]);
}
printf("%d\n",dp[1][n]); //dp[1][n]表示从1到n的最少乘法次数
}
return 0;
}