初识,线段树和树状数组
这几天在网上看了很多关于线段树和树状数组的资料,感觉是很重要的数据结构,有必要边学边做下记录。
1.线段树
凡是关于线段树的资料,我想都有这么一张图,的确,它给了人最初的感性认识,其次这幅图在以后分析问题时也很有帮助:
线段树的基本操作(由于线段树是一棵完全二叉树,且每条线段以类似“二分”的方法处理,因此时间复杂为O(logN)):
typedef struct
{int l , r; // 线段左右端点int cover; // 是否被覆盖
}TreeNode;
TreeNode seg_tree[N];
/* 创建线段树,叶节点为[a,a+1] */
void CreateSegTree( int p , int a , int b)
{
int m;
seg_tree[p].l = a;
seg_tree[p].r = b;
seg_tree[p].cover = 0 ;
m = (a + b) / 2 ;
if (m > a)
{
CreateSegTree( 2 * p , a , m);
CreateSegTree( 2 * p + 1 , m , b);
}
}
/* 插入线段 */
void InsertSegTree( int p , int a , int b)
{
int m;
if (seg_tree[p].l == a && seg_tree[p].r == b)
{
seg_tree[p].cover = 1 ;
return ;
}
m = (seg_tree[p].l + seg_tree[p].r) / 2 ;
/* 插入左子树 */
if (b <= m)
{
InsertSegTree( 2 * p , a , b);
}
/* 插入右子树 */
else if (a >= m)
{
InsertSegTree( 2 * p + 1 , a , b);
}
/* 分插两边 */
else
{
InsertSegTree( 2 * p , a , m);
InsertSegTree( 2 * p + 1 , m ,b);
}
}
/* 删除线段(注意当删除一条线段时,要连同它的子树一起删除 */
/* eg:删除线段(1,5)那么像子线段(1,3),(3,5)之类的线段也要删除) */
int DeleteSegTree( int p , int a , int b)
{
int m , nRet;
if (seg_tree[p].l + 1 == seg_tree[p].r)
{
nRet = seg_tree[p].cover;
seg_tree[p].cover = 0 ;
return nRet;
}
m = (seg_tree[p].l + seg_tree[p].r) / 2 ;
/* 原先完全覆盖 */
if (seg_tree[p].cover == 1 )
{
seg_tree[p].cover = 0 ;
seg_tree[ 2 * p].cover = seg_tree[ 2 * p + 1 ].cover = 1 ;
}
if (b <= m)
{
return DeleteSegTree( 2 * p , a , b);
}
if (a >= m)
{
return DeleteSegTree( 2 * p + 1 , a , b);
}
else
{
return DeleteSegTree( 2 * p , a , m) && DeleteSegTree( 2 * p + 1 , m ,b);
}
}
(这里的叶子结点是[a,a+1],也就是说线段树中的每个节点都是一个区间,叶节点的区间间隔是1,但是还有一种线段树它的划分方法是,[a , m ] 和 [m+1 , b] 它的叶节点是[a,a],我们会根据不同的问题选择不同的线段树)
2.树状数组
以下摘自网上下的一个DOC文件
树状数组是一个查询(某一区间元素和)和修改(某一元素值),时间复杂度都为log(n)的数据结构(普通数组查询和修改的复杂度分别为O(n)和O(1),当数据量非常大时,且需要频繁求和,树状数组就能凸显其高效性),假设数组a[1...n],那么查询a[1] + …… + a[i] 的时间是log级别的,而且是一个在线的数据结构,支持随时修改某个元素的值,复杂度也为log级别。
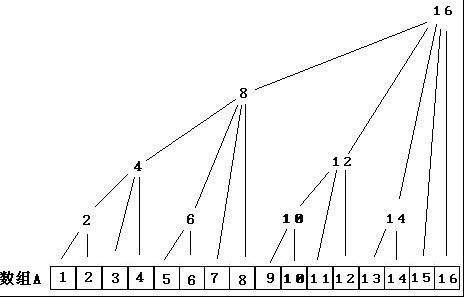
来观察一下这个图:
令这棵树的结点编号为C1,C2……Cn。令每个结点的值为这棵树的值的总和,那么容易发现:
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
……
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
这里有一个有趣的性质,下午推了一下发现:
设节点编号为x,那么这个节点管辖的区间为2^k(其中k为x二进制末尾0的个数)个元素。因为这个区间最后一个元素必然为Ax,所以很明显:
Cn = A(n – 2^k + 1) + …… + An
算这个2^k有一个快捷的办法,定义一个函数如下即可:
int lowbit( int x)
{return x & (x ^ (x – 1 ));
}
当想要查询一个SUM(n)时,可以依据如下算法即可:
step1: 令sum = 0,转第二步;
step2: 假如n <= 0,算法结束,返回sum值,否则sum = sum + Cn,转第三步;
step3: 令n = n – lowbit(n),转第二步。
可以看出,这个算法就是将这一个个区间的和全部加起来,为什么是效率是log(n)的呢?以下给出证明:
n = n – lowbit(n)这一步实际上等价于将n的二进制的最后一个1减去。而n的二进制里最多有log(n)个1,所以查询效率是log(n)的。
那么修改呢,修改一个节点,必须修改其所有祖先,最坏情况下为修改第一个元素,最多有log(n)的祖先。所以修改算法如下(给某个结点i加上x):
step1: 当i > n时,算法结束,否则转第二步;
step2: Ci = Ci + x, i = i + lowbit(i)转第一步。
i = i +lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程。
所以整个程序如下:
int lowbit( int t)
{
return t & (t ^ (t - 1 )); // t&(-t)
}
void modify( int pos , int num)
{
while (pos <= n)
{
in [pos] += num;
pos += lowbit(pos);
}
}
int query( int end)
{
int sum = 0 ;
while (end > 0 )
{
sum += in [end];
end -= lowbit(end);
}
return sum;
}
memset( in , 0 , sizeof ( in )); // 初始化
for (i = 1 ; i <= n ; i ++ ) modify(i, a[i]);