数据结构——AVL树
AVL树是最早提出的自平衡二叉树,在AVL树中任何节点的两个子树的高度最大差别为一,即|HL-HR|<=1,所以它也被称为高度平衡树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
AVL树中查找、插入和删除在平均和最坏情况下都是O(log n),增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。确定并删除标识符为x的元素、及确定并删除第k个最小元素都可以在O(log n)时间内完成。
有四种插入方式会打破树的平衡:
(1)LL:插入一个新节点到根节点的左子树(Left)的左子树(Left),导致根节点的平衡因子由1变为2
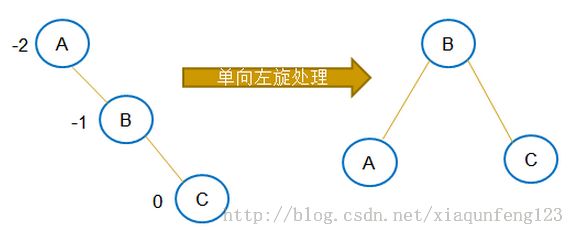
(2)RR:插入一个新节点到根节点的右子树(Right)的右子树(Right),导致根节点的平衡因子由-1变为-2
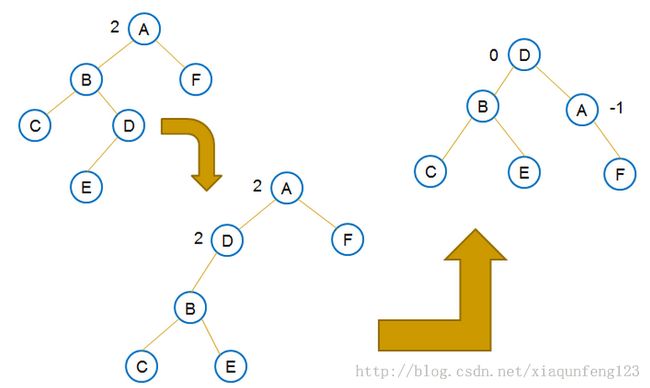
(3)LR:插入一个新节点到根节点的左子树(Left)的右子树(Right),导致根节点的平衡因子由1变为2
(4)RL:插入一个新节点到根节点的右子树(Right)的左子树(Left),导致根节点的平衡因子由-1变为-2
针对四种种情况可能导致的不平衡,可以通过旋转使之变平衡。有两种基本的旋转:
(1)左旋转:将根节点旋转到(根节点的)右孩子的左孩子位置
(2)右旋转:将根节点旋转到(根节点的)左孩子的右孩子位置
注意:旋转需要保证的是该数的中序遍历节点的顺序不变!基本的数据结构:
typedef struct BSTNode
{
int data;
int bf; //结点的平衡因子
struct BSTNode *lchild,*rchild;//左、右孩子指针
}BSTNode,*BSTree;
右旋转:
代码如下:
//对以*p为根的二叉排序树作右旋处理,LL型平衡旋转法
void R_Rotate(BSTree &p)
{
BSTree lc;
lc = p->lchild; //lc指向的*p左子树根结点
p->lchild = lc->rchild; //lc的右子树挂接为*p的左子树
lc->rchild = p;
p = lc; //p指向新的结点
}
左旋转:
代码如下:
//对以*p为根的二叉排序树作左旋处理,RR型平衡旋转法
void L_Rotate(BSTree &p)
{
BSTree rc;
rc = p->rchild; //rc指向的*p右子树根结点
p->rchild = rc->lchild; //rc的左子树挂接为*p的右子树
rc->lchild = p;
p = rc; //p指向新的结点
}
先左旋、后右旋:
代码如下:
//对以指针T所指结点为根的二叉树作左平衡旋转处理,LR型平衡旋转法
void LeftBalance(BSTree &T)
{
BSTree lc,rd;
lc = T->lchild; //lc指向*T的左子树根结点
switch(lc->bf) //检查*T的左子树的平衡度,并作相应平衡处理
{
case LH: //新结点插入在*T的左孩子的左子树上,要作单右旋处理
T->bf = lc->bf = EH;
R_Rotate(T); break;
case RH: //新结点插入在*T的左孩子的右子树上,要作双旋处理
rd = lc->rchild; //rd指向*T的左孩子的右子树根
switch(rd->bf) //修改*T及其左孩子的平衡因子
{
case LH:T->bf = RH; lc->bf = EH; break;
case EH:T->bf = lc->bf = EH; break;
case RH:T->bf = EH; lc->bf = LH; break;
}
rd->bf = EH;
L_Rotate(T->lchild); //对*T的左子树作左旋平衡处理
R_Rotate(T); //对*T作右旋平衡处理
}
}
先右旋转后左旋转
同上。
插入操作:就是在不同情况下采用旋转方式调整AVL树的平衡
代码如下:
//插入结点e,若T中不存在和e相同关键字的结点,则插入一个数据元素为e的新结点,并返回1,否则返回0
bool InsertAVL(BSTree &T,int e,bool &taller)
{
if(!T)//插入新结点,树"长高",置taller为true
{
T = (BSTree)malloc(sizeof(BSTNode));
T->data = e;
T->lchild = T->rchild =NULL;
T->bf = EH; taller = true;
}
else
{
if(EQ(e,T->data)) //树中已存在和有相同关键字的结点则不再插入
{
taller = false;
printf("The node have already exist!\n");
return 0;
}
if(LT(e,T->data)) //应继续在*T的左子树中进行搜索
{
if(!InsertAVL(T->lchild,e,taller))
return 0;//未插入
if(taller) //已插入到*T的左子树中且左子树"长高"
{
switch(T->bf) //检查*T的平衡度
{
case LH: //原本左子树比右子树高,需要作左平衡处理
LeftBalance(T);
taller = false; break;
case EH: //原本左子树、右子等高,现因左子树增高而使树增高
T->bf = LH;
taller = true; break;
case RH: //原本右子树比左子树高,现左、右子树等高
T->bf = EH;
taller = false; break;
}
}
}
else //应继续在*T的右子树中进行搜索
{
if(!InsertAVL(T->rchild,e,taller))
return 0;//未插入
if(taller) //已插入到*T的右子树中且右子树"长高"
{
switch(T->bf) //检查*T的平衡度
{
case LH: //原本左子树比右子树高,现左、右子树等高
T->bf = EH; taller = false; break;
case EH: //原本左子树、右子等高,现因右子树增高而使树增高
T->bf = RH; taller = true; break;
case RH: //原本右子树比左子树高,需要作右平衡处理
RightBalance(T); taller = false; break;
}
}
}
}
return 1;
}//InsertAVL
代码如下:
删除节点时左平衡旋转操作处理:
//删除结点时左平衡旋转处理
void LeftBalance_div(BSTree &p,int &shorter)
{
BSTree p1,p2;
if(p->bf==1) //p结点的左子树高,删除结点后p的bf减1,树变矮
{
p->bf=0; shorter=1;
}
else if(p->bf==0)//p结点左、右子树等高,删除结点后p的bf减1,树高不变
{
p->bf=-1; shorter=0;
}
else //p结点的右子树高
{
p1=p->rchild;//p1指向p的右子树
if(p1->bf==0)//p1结点左、右子树等高,删除结点后p的bf为-2,进行左旋处理,树高不变
{
L_Rotate(p);
p1->bf=1;
p->bf=-1;
shorter=0;
}
else if(p1->bf==-1)//p1的右子树高,左旋处理后,树变矮
{
L_Rotate(p);
p1->bf=p->bf=0; shorter=1;
}
else //p1的左子树高,进行双旋处理(先右旋后左旋),树变矮
{
p2=p1->lchild;
p1->lchild=p2->rchild; p2->rchild=p1; p->rchild=p2->lchild; p2->lchild=p;
if(p2->bf==0)
{
p->bf=0; p1->bf=0;
}
else if(p2->bf==-1)
{
p->bf=1;p1->bf=0;
}
else
{
p->bf=0;
p1->bf=-1;
}
p2->bf=0;
p=p2;
shorter=1;
}
}
}删除节点时右旋转操作处理:
//删除结点时右平衡旋转处理
void RightBalance_div(BSTree &p,int &shorter)
{
BSTree p1,p2;
if(p->bf==-1)
{
p->bf=0; shorter=1;
}
else if(p->bf==0)
{
p->bf=1; shorter=0;
}
else
{
p1=p->lchild;
if(p1->bf==0)
{
R_Rotate(p);
p1->bf=-1; p->bf=1; shorter=0;
}
else if(p1->bf==1)
{
R_Rotate(p);
p1->bf=p->bf=0; shorter=1;
}
else
{
p2=p1->rchild;
p1->rchild=p2->lchild; p2->lchild=p1; p->lchild=p2->rchild; p2->rchild=p;
if(p2->bf==0)
{
p->bf=0;
p1->bf=0;
}
else if(p2->bf==1)
{
p->bf=-1;
p1->bf=0;
}
else
{
p->bf=0; p1->bf=1;
}
p2->bf=0; p=p2; shorter=1;
}
}
}
代码已上传,可下载:http://download.csdn.net/detail/xiaqunfeng123/7217297
参考资料: http://zh.wikipedia.org/wiki/AVL%E6%A0%91
http://dongxicheng.org/structure/avl/
http://dongxicheng.org/structure/avl/
部分图片来源: http://blog.csdn.net/jkay_wong/article/details/6676488