POJ 1179 Polygon

Polygon

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2770		Accepted: 1129

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N. 

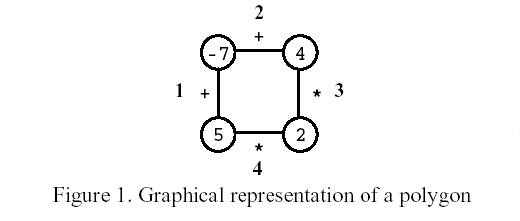
On the first move, one of the edges is removed. Subsequent moves involve the following steps: 
�pick an edge E and the two vertices V1 and V2 that are linked by E; and 
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. 
The game ends when there are no more edges, and its score is the label of the single vertex remaining. 

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0. 

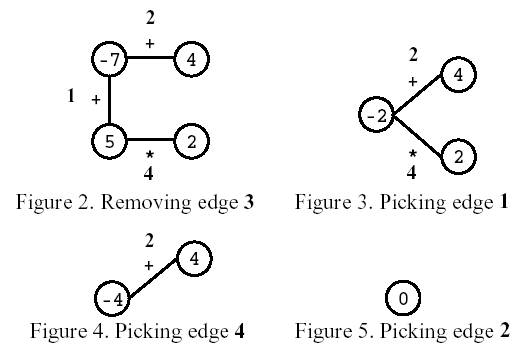
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score. 

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *). 

3 <= N <= 50 
For any sequence of moves, vertex labels are in the range [-32768,32767]. 

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

Source

IOI 1998

/*
http://acm.pku.edu.cn/JudgeOnline/problem?id=1179
枚举 + 分段DP
枚举所有边来删除，然后从删除的边右侧的起始点开始分段DP,对于乘法
由于可能负负得正，因此需要考虑所有min和max的组合情况
(1)对于加法
max[i][j] = max(max[i][j], max[i][k] + max[k+1][j]), i <= k < j
min[i][j] = min(min[i][j], min[i][k] + min[k+1][j]), i <= k < j
(2)对于乘法
max[i][j] = max(max[i][j], min[i][k] * min[k + 1][j], min[i][k] * max[k + 1][j],
                           max[i][k] * min[k + 1][j], max[i][k] * max[k + 1][j]), i <= k < j
min[i][j] = min(min[i][j], min[i][k] * min[k + 1][j], min[i][k] * max[k + 1][j],
                           max[i][k] * min[k + 1][j], max[i][k] * max[k + 1][j]), i <= k < j
另外每次DP在分段时由于起始位置不一定0，所以要注意边界转换问题
*/
#include <iostream>
#define MAX_N 50
#define MAX_VAL 32770
#define MIN_VAL -32770
#define maxv(a, b) ((a) >= (b) ? (a) : (b))
#define minv(a, b) ((a) <= (b) ? (a) : (b))
using namespace std;

//存储当前点的权值
int val[MAX_N + 1];
//存储当前点左侧的边上的操作符
char op[MAX_N + 1];

//DP统计每段的最大值和最小值
int minVal[MAX_N + 1][MAX_N + 1];
int maxVal[MAX_N + 1][MAX_N + 1];
int n;

//所能达到的最大值
int maxRes = MIN_VAL;
//标记删除哪些边可以达到这个最大值
bool maxPos[MAX_N + 1];

//初始化，DP初始条件是max[i][i] = min[i][i] = i结点的权值
void init()
{
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
        {
            if(i == j)
                minVal[i][j] = maxVal[i][j] = val[i];
            else
            {
                minVal[i][j] = MAX_VAL;
                maxVal[i][j] = MIN_VAL;
            }
        }
}

//删除p结点之前的边，并进行DP计算
int dpSolve(int p)
{
    char c;
    int len, i, j, k, index_i, index_j, index_k;
    //遍历表达式长度(即表达式中结点的个数)
    for(len = 2; len <= n; len++)
    {
        //遍历在len长度下，可以达到的起始位置
        for(i = p; i <= n + p - len; i++)
        {
            //j是终止位置
            j = i + len - 1;
            //对ij进行分段
            for(k = i; k < j; k++)
            {
                //边界转换
                index_i = i % n;
                index_j = j % n;
                index_k = k % n;

                //分段处的操作符
                c = op[(index_k + 1) % n];

                //得到两段各自的最小值和最大值
                int minik = minVal[index_i][index_k];
                int maxik = maxVal[index_i][index_k];
                int minkj = minVal[(index_k + 1) % n][index_j];
                int maxkj = maxVal[(index_k + 1) % n][index_j];
                int minTemp, maxTemp;
                if(c == 't')
                {
                    maxTemp = maxik + maxkj;
                    minTemp = minik + minkj;
                }
                else
                {
                    int max1 = maxv(minik * minkj, minik * maxkj);
                    int max2 = maxv(maxik * minkj, maxik * maxkj);
                    maxTemp = maxv(max1, max2);

                    int min1 = minv(minik * minkj, minik * maxkj);
                    int min2 = minv(maxik * minkj, maxik * maxkj);
                    minTemp = minv(min1, min2);
                }
                //得到段ij的最小值和最大值
                maxVal[index_i][index_j] = maxv(maxTemp, maxVal[index_i][index_j]);
                minVal[index_i][index_j] = minv(minTemp, minVal[index_i][index_j]);
            }
        }
        //返回本次DP表达式的最大值
        if(len == n)
            return maxVal[p][(p + n - 1) % n];
    }
}
int main()
{   
    int i;
    cin>>n;
    for(i = 0; i < n; i++)
        cin>>op[i]>>val[i];

    //枚举删除的边的位置
    for(i = 0; i < n; i++)
    {
        init();
        int curVal = dpSolve(i);
        if(curVal > maxRes)
        {
            maxRes = curVal;
            memset(maxPos, 0, sizeof(maxPos));
            maxPos[i] = true;
        }
        else if(curVal == maxRes)
            maxPos[i] = true;
    }
    cout<<maxRes<<endl;
    for(i = 0; i < n; i++)
    {
        if(maxPos[i])
         cout<<i + 1<<" ";
    }
    cout<<endl;
    return 0;
}