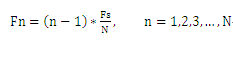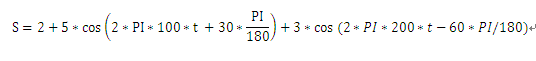傅里叶变换的物理意义

假设信号的采样频率是Fs，信号的频率是F，采样点数为N，则与傅里叶变换相关概念几个计算公式如下：

1.      频率计算公式

                                                                                                            

2.      振幅计算公式 Magnitude

                

     

3.       相位计算公式Pan

                          

 

 

示例：假设有如下两个交流信号，以512的采样率对信号进行采样，采样点数也为512点。

     信号1:  2V的直流分量，幅度为5V，频率为100hz，相位为30度。

     信号2：幅度为3V，频率为200hz，相位为-60度。

用数学表达式来描述如下：

                                                               

下面的matlab脚本画出其频谱图：

>>N_data_size = 512;
>> t = [0:1:N_data_size];
>> fs = 512;
>> t = t/fs;
>> s = 2 + 5 * cos(2 * pi * 100 * t +30 * pi / 180) + 3 * cos(2 * pi * 200 * t-60 * pi / 180);
>> M = abs(fft(s,N_data_size));
>> plot(M);

                              
                                   

 

 

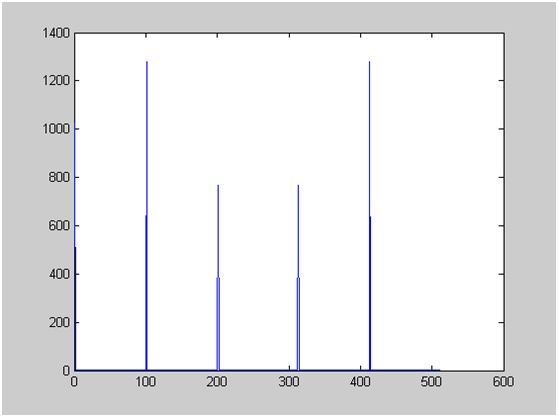
因采样点数等于采样频率，因此两个点之间的频率间隔是1Hz。按照频率计算公式Fn=(n-1)*FS/N计算，第n个点的频率就是n-1.因此第101个点的频谱就是100，对应于原始信号第一个交流信号的频率，第201个点的频率是200，对应于第二个交流信号的频率。由此可知，图像应该在第0,101,201三个点上出现峰值。从上面的图看，确实是这样。注意，频谱图关于奈奎斯特频率是对称的，所以只看奎斯特频率以下的部分就可以了。

 

根据前面的公式，第一个点的模值为直流分量*N = 2 *512 = 1024；

第一个原始信号的峰值为A =5，因此它的模值为 A * N/2= 5 * 512/2 = 1280;

第二个原始信号的峰值为A=3，因此它的模值为 A * N/2 =3 * 512/2 = 768;

 

分别拿出这三个点的FFT结果来细看：

第一个点的FFT结果： 1024 + 0* i , A1 = sqrt(1024*1024) = 1024;

第二个点的FFT结果：1108.5+640*I,A101 = sqrt(1108.5*1108.5+640*640) = 1280;

第三个点的FFT结果：384-665.11i,A201= sqrt(384*384+665.11*665.11) = 768;

 

由此可见，如果知道了每个频率点信号的峰值和采样点数，那么很容易计算出它的模值。反过来也是如此，即如果用FFT计算出了信号的模值，也很容易计算出原始信号的峰值。例如，对于上例：直流分量的值：A= A1/N = 1024/512 = 2;

交流信号1的幅度为：A =A101/N/2=1280*2/512=5;

交流信号2的幅度为：A=A201/N/2=768*2/512=3.

相位的计算就更简单，从略。