HDU 1992Tiling a Grid With Dominoes(状压dp)

Tiling a Grid With Dominoes

Time Limit: 1000/500 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 410    Accepted Submission(s): 321

Problem Description

We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.



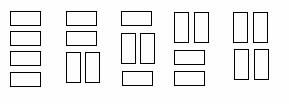
Write a program that takes as input the width, W, of the grid and outputs the number of different ways to tile a 4-by-W grid.

 

Input

The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.
Each dataset contains a single decimal integer, the width, W, of the grid for this problem instance.

 

Output

For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.

 

Sample Input

   
   
   
   

    
    
    
    3
2
3
7
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    1 5
2 11
3 781
   
   
   
   

 

Source

2008 “Shun Yu Cup” Zhejiang Collegiate Programming Contest - Warm Up（1）

 

Recommend

linle   |   We have carefully selected several similar problems for you:   1988  1993  1985  1986  1987 

 

题目大意：题目意思是有一块4*N(1 ≤ N ≤ 1000)实际上n不会超过21的空地。你只有1*2的砖。问你铺满这块区域有多少种方法。

    解题思路：

    自己在那里乱搞递推公式，状压dp的思想很不错，博博讲的很精辟。我们算成n行的砖，每行有四。然后用4个01位表示一行，如果是0表示这一行不会占用下一行的地方，如果是1表示会占用下一行的砖。这样想想就比较容易了。状态转移有三种：

1，当前行当前位为1，那么直接转移到下一位。

2，当前行当前位为0，那么可以表示下一行可以为1.

3，当前行当前位和下一位为00，那么下一行也可以为00。

   详见AC代码：

    题目地址：http://acm.hdu.edu.cn/showproblem.php?pid=1992

博博详解：http://blog.csdn.net/bossup/article/details/21948079

AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
using namespace std;

int dp[1005][16];

void dfs(int r,int c,int cur,int nex)
//分别表示当前行，当前列,当前状态，可转移的状态
{
    if(c>3)
    {
        dp[r+1][nex]+=dp[r][cur];
        return;
    }
    if(!(cur&(1<<c)))
    {
        dfs(r,c+1,cur,nex|(1<<c));   //竖着放，用1
        if(c<=2&&!(cur&(1<<(c+1))))
            dfs(r,c+2,cur,nex);  //也可以横着放，两个0
    }
    else
        dfs(r,c+1,cur,nex);   //位置被上面的占了
}

int main()
{
    memset(dp,0,sizeof(dp));
    dp[0][0]=1;
    int i,j;
    for(i=0;i<22;i++)   //22已经爆int32了
        for(j=0;j<16;j++)
            if(dp[i][j])
                dfs(i,0,j,0);

    int tes,x;
    cin>>tes;

    for(i=1;i<=tes;i++)
    {
        cin>>x;
        cout<<i<<" "<<dp[x][0]<<endl;
    }
    return 0;
}