活动安排问题(贪心算法)
类似的问题是:选点问题和区间覆盖问题。
活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合,是可以用贪心算法有效求解的很好例子。该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。
设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi 。如果选择了活动i,则它在半开时间区间[si, fi]内占用资源。若区间[si, fi]与区间[sj, fj]不相交,则称活动i与活动j是相容的。也就是说,当si≥fj或sj≥fi时,活动i与活动j相容。
由于输入的活动以其完成时间的非减序排列,所以算法greedySelector每次总是选择具有最早完成时间的相容活动加入集合A中。直观上,按这种方法选择相容活动为未安排活动留下尽可能多的时间。也就是说,该算法的贪心选择的意义是使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。
此算法的效率极高。当输入的活动已按结束时间的非减序排列,算法只需O(n)的时间安排n个活动,使最多的活动能相容地使用公共资源。如果所给出的活动未按非减序排列,可以用O(nlogn)的时间重排。
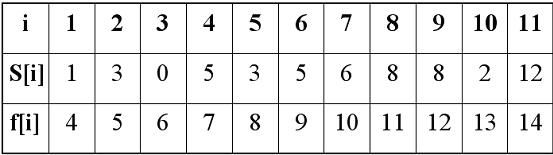
例:设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下:
算法的计算过程如图所示。图中每行相应于算法的一次迭代。阴影长条表示的活动是已选入集合A的活动,而空白长条表示的活动是当前正在检查相容性的活动。
若被检查的活动i的开始时间Si小于最近选择的活动j的结束时间fi,则不选择活动i,否则选择活动i加入集合A中。
贪心算法并不总能求得问题的整体最优解。但对于活动安排问题,贪心算法却总能求得的整体最优解,即它最终所确定的相容活动集合A的规模最大。这个结论可以用数学归纳法证明。
//活动安排问题
public class Activearr
{
public static int greedselector(int [] s,int [] f,boolean [] a)
{
int n = s.length - 1;
a [0] = true;
int j = 1;
int count = 1;
for (int i = 1;i <= n;i ++)
{
if (s [i] >= f [j])
{
a [i] = true;
j = i;
count ++;
}
else a [i] = false;
}
return count;
}
public static void main(String args [])
{
int count;
int s [] = {1,3,0,5,3,5,6,8,8,2,12};
int f [] = {4,5,6,7,8,9,10,11,12,13,14};
boolean a [] = new boolean [11];
Activearr aa = new Activearr();
count = aa.greedselector(s,f,a);
System.out.println("共有" + count + "活动可以举行:");
System.out.println();
for (int i = 0;i <= 10;i ++)
if (a [i] == true)
System.out.println("第" + i + "活动可以举行");
}
}
如果每个活动的价值不一样。例如下面这道题:
一个人在网上做项目,加入每天都有很多项目可以选,每个项目都有一个开始时间和截止时间,假设每个项目的钱是一样的,那么在n天内,如何安排自己的接活才能保证赚钱最多。问题简化后就是贪心的活动安排问题, 传送门:http://blog.csdn.net/a9529lty/article/details/4042019假如这个时候,每个活的钱数是不同的,可以获得最大的钱数是多少?
代码如下:
#define MAX_TAST 100
struct Task{
int s, e;
int val;
};
bool TaskInRange(const Task &t, int s, int e){
return t.s >= s && t.e <= e;
}
int dp[MAX_TAST][MAX_TAST];
int nTask;
Task aTask[nTask];
int GetMaxValue(int s, int e){
if(dp[s][e] != -1){
return dp[s][e];
}
if( s == e){
return dp[s][e] = 0;
}
int maxvalue = 0;
for(int i = 0; i < nTask; i++){
if(TaskInRange(aTask[i], s, e))
{
int value = GetMaxValue(s, aTask[i].s) +
GetMaxValue(aTask[i].e, e) +
aTask[i].val;
if(value > maxvalue){
maxvalue = value;
}
}
}
return dp[s][e] = maxvalue;
}
如何优化:可以先把任务排序,然后搜索到合适的任务岂止点,将枚举从O(n)降低到O(logn).
其实,本题还可以用动态规划来做。思路如下:
设这些tasks最早开始于0,最晚结束于T。V[t]表示从t到T最多能赚的钱。设所有开始时间大于等于t的tasks的集合设为tasks[t],那么
V[t] = max ( v[task] + V[endtime(task)] ) for task in tasks[i]
v[task]表示做task可以挣的钱。