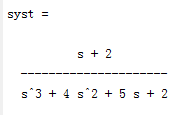基于Matlab的控制系统仿真实例

以弹簧自身质量不可忽略的阻尼器系统为例，通过Matlab的Control System Toolbox讲解控制系统的仿真，设弹簧控制系统的框图如下：

取m=1,k=1,c=2。

1、建立传递函数：

 m=1;k=1;c=2;
G1=tf(1,[1,0]);
H=tf(k,[m,c]);
ph=feedback(G1,H);
G2=tf(1,[m,c]);
syst=G2*ph;%传递函数
[A,B,C,D]=ssdata(syst);
syss=ss(A,B,C,D);%或syss=ss(syst)  %状态空间表达式
syszp=zpk(syst);%零-极-增益模型

2、系统响应

t=0:.2:15;
y=impulse(syss,t);%冲激响应
figure(1)
plot(t,y,'r'),grid

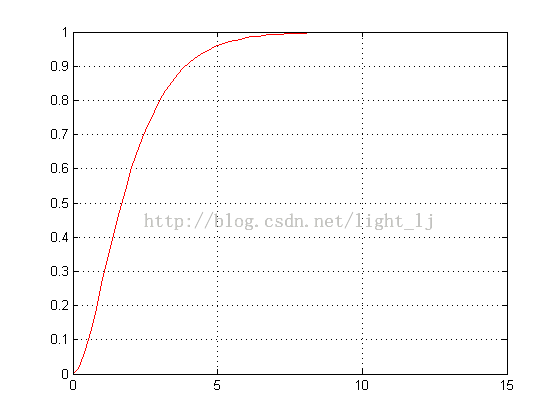
y=step(syss,t);%阶跃响应
figure(2)
plot(t,y,'r'),grid

t=0:0.01:5;%自定义输入响应
u=sin(t);
lsim(syss,u,t)
%系统对由u和t描述的自定义输入信号的响应。对MIMO系统，u是一个矩阵，第i行是输人信号在T（i）时刻的值

3、留数定理

disp('Residue Form')
[num,den]=tfdata(syst);
num=num{1};den=den{1};%将元胞数组转化成向量
[r,p,k]=residue(num,den)
disp('hit any key to continue'),pause

4、频域仿真

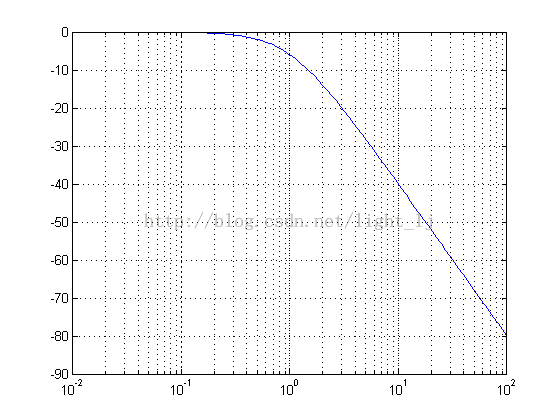
w=logspace(-2,2,100);%定义频率的对数区间
[re,im]=nyquist(syss,w);%state space形式，w可省略
 re1=re(:);im1=im(:);
g=re1+i*im1;
mag=20*log10(abs(g));%幅值
phase=angle(g)*180/pi;%相角
semilogx(w,mag,'b') %%幅值曲线

 semilogx(w,phase,'b'),grid  %相角曲线

nyquist(systf),grid  %绘制奈奎斯特图，或者用plot(re1,im1）

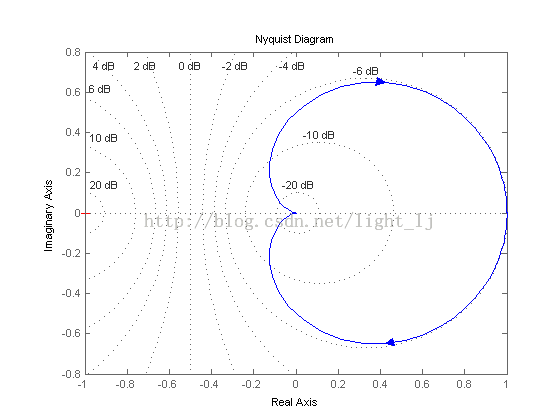
暂时到这吧，日后有需要再更新。。。