自己动手写二叉堆

一、二叉堆概念

二叉堆一种数组对象，可以被视为一棵完全二叉树，树中每个结点和数组中存放该结点值的那个元素对应。树的每一层都是填满的，最后一层除外。表示堆的数组有两个属性对象，其中length[A]表示数组A中的元素个数，而heap-size[A]则表示存放在A中的堆的元素个数。heap-size[A]<=length[A]，也就是说虽然A[1....length[A]]都可以包含有效值，但是A[heap-size[A]]之后的元素不属于相应的堆。树的根为A[1]，给定某个结点的下标i，可以很容易计算它的父亲结点和儿子结点。注:本文代码中数组A都是从位置1开始存储，位置0废弃不用，因为从1开始存储便于描述和理解。

int parent(int i) { return i/2; }

int left(int i) { return 2*i; }

int right(int i) { return 2*i + 1; }

扩展：

堆对应的树每一层都是满的，所以一个高度为h的堆中，元素数目最多为1+2+2^2+...2^h = 2^(h+1) - 1(满二叉树)，元素数目最少为1+2+...+2^(h-1) + 1 = 2^h。

由于元素数目2^h  <= n <= 2^(h+1) -1，所以 h <= lgn < h+1，因此h = lgn 。即一个包含n个元素的二叉对高度为lgn。

二、保持堆的性质

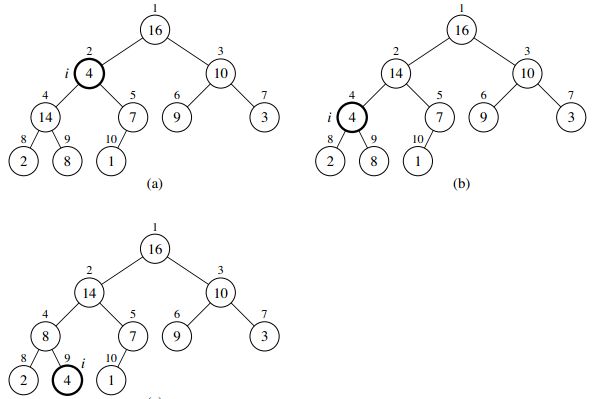
本文主要建立一个最大堆，最小堆原理类似，为了保持堆的性质，heapify(A, i, heapsize)函数让A[i]在最大堆中下降，使得以i为根的子树成为最大堆。在算法每一步里，从元素A[i]和A[left]以及A[right]中选出最大的，将其下标存在largest中。如果A[i]最大，则以i为根的子树已经是最大堆，程序结束。否则，i的某个子结点有最大元素，将A[i]与A[largest]交换，从而使i及其子女满足最大堆性质。此外，下标为largest的结点在交换后值变为A[i]，以该结点为根的子树又有可能违反最大堆的性质，所以要对该子树递归调用max_heapify函数。当max_heapify函数作用在一棵以i为根结点的、大小为n的子树上时，运行时间为调整A[i]、A[left]、A[right]的时间为O(1)，加上对以i为某个子结点为根的子树递归调用max_heapify的时间。i结点为根的子树大小最多为2n/3，所以可以推得T(N) <= T(2N/3) + O(1)，所以T(N)=O(lgN)。

void max_heapify(int A[], int i, int heapsize)
{
    int l = left(i); //左孩子的位置
    int r = right(i); //右孩子的位置
    int largest = i;
    if (l<=heapsize && A[l]>A[i])
        largest = l;
    if (r<=heapsize && A[r]>A[largest])
        largest = r;
    if (largest != i) {  //如果最大值不等于A[i]，则交换A[i]和A[largest]，并让largest保持堆的性质
        swap(A, i, largest);
        max_heapify(A, largest, heapsize);
    }
}

下图是一个运行heapify(A，2， heapsize)的例子。A={16 ，4 ，10 ，14 ，7 ，9 ，3 ，2 ，8 ，1 }，heapsize=10。

三、建立最大堆

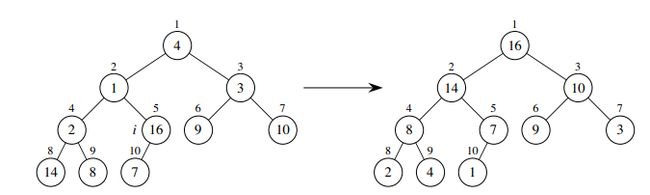
 我们可以知道，数组A[1,2...N]中，A[N/2+1...N]的元素都是树的叶结点。如上面图中的6-10的结点都是叶结点。每个叶子结点可以看作是只含一个元素的最大堆，因此我们只需要对其他的结点调用max_heapify函数即可。

void build_max_heap(int A[], int N)
{
    int heapsize = N;
    for (int i = N/2; i >= 1; i--) { //对N/2~1的结点调用max_heapify
        max_heapify(A, i, heapsize);
    }
}

还是使用与上面同样的数组A建立最大堆，最终建立的最大堆如下面右图所示：

之所以这个函数是正确的，我们需要来证明一下，还是使用循环不变式来证明。

循环不变式：在for循环开始前，结点i+1、i+2...N都是一个最大堆的根。

初始化：for循环开始迭代前，i=N/2, 结点N/2,  N/2+1，N/2+2...N都是叶结点，也都是最大堆的根。

保持：因为结点i的子结点标号都比i大，根据循环不变式的定义，这些子结点都是最大堆的根，所以调用max_heapify后，i成为了最大堆的根，而i+1、i+2...N仍然保持最大堆的性质。

终止：过程终止时，i=0，因此结点1、2、...N都是最大堆的根，特别的，结点1就是一个最大堆的根。

虽然每次调用max_heapify时间为O(lgN)，共有O(N)次调用，但是说运行时间是O(NlgN)是不确切的，准确的来说，运行时间为O(N)，这里就不证明了，具体证明过程参见《算法导论》。

四、堆排序

开始用build_max_heap函数创建一个最大堆，因为数组最大元素在A[1]，通过直接将它与A[N]互换来达到最终正确位置。去掉A[N]，堆的大小heapsize减1，调用max_heapify(A, 1, heapsize)保持最大堆的性质，直到堆的大小由N减到2。

void heap_sort(int A[], int N)
{
    build_max_heap(A, N); //建立最大堆
    int heapsize = N;
    for (int i=N; i>=2; i--) { 
        swap(A, 1, i); //交换
        heapsize--;  //堆大小减1
        max_heapify(A, 1, heapsize); //保持
    }
}

五、优先级队列

最后实现一个最大优先级队列，主要有四种操作，分别如下所示：

1）INSERT(S， x)：将x插入到集合S中。

2）MAXIMUM(S): 返回S中最大关键字的元素

3）EXTRACT-MAX(S)：去掉并返回S中最大关键字的元素

4）INCREASE-KEY(S, x, k)：将元素x的关键字的值增加到k，注意k不能小于x。

分别实现如下：

int maximum(int A[])
{
    return A[1];
}

int extract_max(int A[], int &heapsize)
{
    assert(heapsize >= 1);
    int max = A[1]; //取最大值A[1]
    A[1] = A[heapsize]; //替换A[1]为A[heapsize]
    heapsize--; //堆大小减1
    max_heapify(A, 1, heapsize); //保持堆的性质
    return max; //返回最大值
}

void heap_increase_key(int A[], int i, int key)
{
    assert(key >= A[i]);
    A[i] = key; //A[i]的关键字增加为key
    while (i>1 && A[parent(i)]<A[i]) { //如果还没有到根结点且父结点关键字小于A[i]
        swap(A, i, parent(i));         //交换A[i]和A[parent(i)]
        i = parent(i);                 //i向上移
    }
}

void max_heap_insert(int A[], int key, int &heapsize)
{
    heapsize++;
    A[heapsize] = INT_MIN;
    heap_increase_key(A, heapsize, key);
}

可以直接使用max_heap_insert来创建一个二叉最大堆。如使用下面代码直接对数组A建立最大堆。

int heapsize = 0;
for (int i=1; i<=N; i++) {
        max_heap_insert(A, A[i], heapsize);//当然最好是用另外的空间建立堆，否则会破坏原来数组A的结构
}