SkipList跳表的原理与实现

为什么选择跳表

目前经常使用的平衡数据结构有：B树，红黑树，AVL树，Splay Tree, Treep等。

 

想象一下，给你一张草稿纸，一只笔，一个编辑器，你能立即实现一颗红黑树，或者AVL树

出来吗？ 很难吧，这需要时间，要考虑很多细节，要参考一堆算法与数据结构之类的树，

还要参考网上的代码，相当麻烦。

 

用跳表吧，跳表是一种随机化的数据结构，目前开源软件 Redis 和 LevelDB 都有用到它，

它的效率和红黑树以及 AVL 树不相上下，但跳表的原理相当简单，只要你能熟练操作链表，

就能轻松实现一个 SkipList。

 

有序表的搜索

考虑一个有序表：

 

从该有序表中搜索元素 < 23, 43, 59 > ，需要比较的次数分别为 < 2, 4, 6 >，总共比较的次数

为 2 + 4 + 6 = 12 次。有没有优化的算法吗?  链表是有序的，但不能使用二分查找。类似二叉

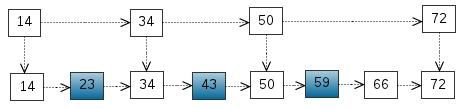
搜索树，我们把一些节点提取出来，作为索引。得到如下结构：

 这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引，这样搜索的时候就可以减少比较次数了。

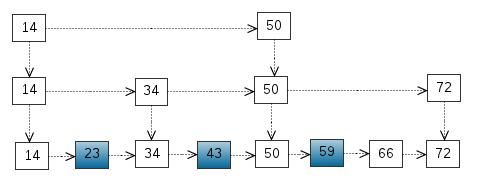
 我们还可以再从一级索引提取一些元素出来，作为二级索引，变成如下结构：

 

  

 

     这里元素不多，体现不出优势，如果元素足够多，这种索引结构就能体现出优势来了。

 

跳表

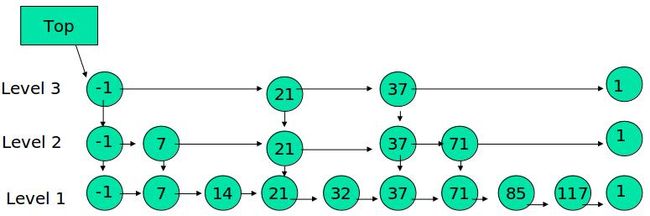
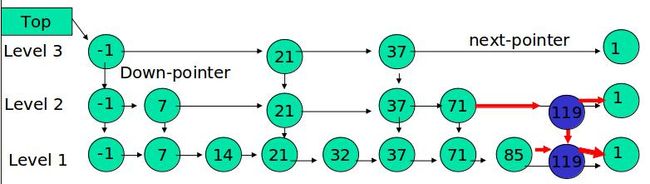
下面的结构是就是跳表：

 其中 -1 表示 INT_MIN， 链表的最小值，1 表示 INT_MAX，链表的最大值。

 

 

跳表具有如下性质：

(1) 由很多层结构组成

(2) 每一层都是一个有序的链表

(3) 最底层(Level 1)的链表包含所有元素

(4) 如果一个元素出现在 Level i 的链表中，则它在 Level i 之下的链表也都会出现。

(5) 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

 

跳表的搜索

 

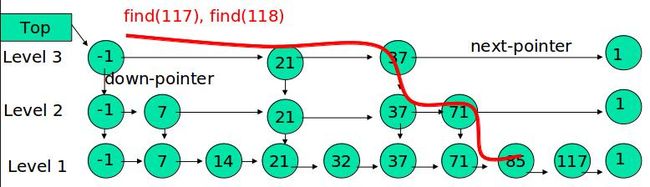
例子：查找元素 117

(1) 比较 21， 比 21 大，往后面找

(2) 比较 37,   比 37大，比链表最大值小，从 37 的下面一层开始找

(3) 比较 71,  比 71 大，比链表最大值小，从 71 的下面一层开始找

(4) 比较 85， 比 85 大，从后面找

(5) 比较 117， 等于 117， 找到了节点。

 

具体的搜索算法如下： 

 

 /* 如果存在 x, 返回 x 所在的节点，
  * 否则返回 x 的后继节点 */
 find(x)
 {
     p = top;
     while (1) {
         while (p->next->key < x)
             p = p->next;
         if (p->down == NULL)
             return p->next;
         p = p->down;
     }
 }

 

 

跳表的插入

先确定该元素要占据的层数 K（采用丢硬币的方式，这完全是随机的）

然后在 Level 1 ... Level K 各个层的链表都插入元素。

例子：插入 119， K = 2

 

如果 K 大于链表的层数，则要添加新的层。

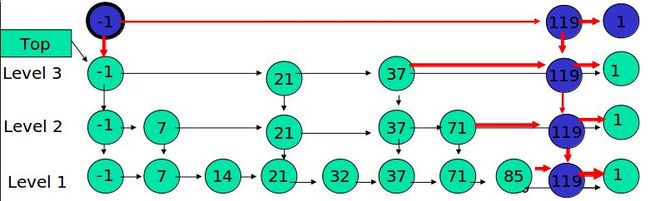
例子：插入 119， K = 4

丢硬币决定 K

插入元素的时候，元素所占有的层数完全是随机的，通过一下随机算法产生：

 

 int random_level()
 {
     K = 1;

     while (random(0,1))
         K++;

     return K;
 }

 

相当与做一次丢硬币的实验，如果遇到正面，继续丢，遇到反面，则停止，

用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布，

K 的期望值 E[K] = 1/p = 2. 就是说，各个元素的层数，期望值是 2 层。

 

 

跳表的高度。

n 个元素的跳表，每个元素插入的时候都要做一次实验，用来决定元素占据的层数 K，

跳表的高度等于这 n 次实验中产生的最大 K，待续。。。

 

跳表的空间复杂度分析

根据上面的分析，每个元素的期望高度为 2， 一个大小为 n 的跳表，其节点数目的

期望值是 2n。

 

跳表的删除

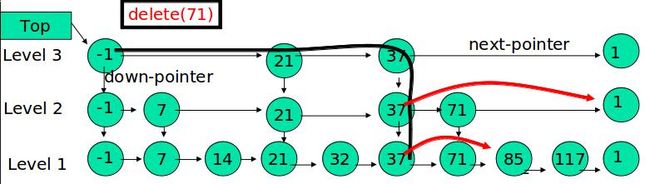
在各个层中找到包含 x 的节点，使用标准的 delete from list 方法删除该节点。

例子：删除 71

上文来自：http://kenby.iteye.com/blog/1187303

实现源代码

/* 

Example of Skip List source code for C:

Skip Lists are a probabilistic alternative to balanced trees, as
described in the June 1990 issue of CACM and were invented by 
William Pugh in 1987. 

This file contains source code to implement a dictionary using 
skip lists and a test driver to test the routines.

A couple of comments about this implementation:
  The routine randomLevel has been hard-coded to generate random
  levels using p=0.25. It can be easily changed.
  
  The insertion routine has been implemented so as to use the
  dirty hack described in the CACM paper: if a random level is
  generated that is more than the current maximum level, the
  current maximum level plus one is used instead.

  Levels start at zero and go up to MaxLevel (which is equal to
	(MaxNumberOfLevels-1).

The compile flag allowDuplicates determines whether or not duplicates
are allowed. If defined, duplicates are allowed and act in a FIFO manner.
If not defined, an insertion of a value already in the file updates the
previously existing binding.

BitsInRandom is defined to be the number of bits returned by a call to
random(). For most all machines with 32-bit integers, this is 31 bits
as currently set. 

The routines defined in this file are:

  init: defines NIL and initializes the random bit source 

  newList: returns a new, empty list 

  freeList(l): deallocates the list l (along with any elements in l)

  randomLevel: Returns a random level

  insert(l,key,value): inserts the binding (key,value) into l. If 
	allowDuplicates is undefined, returns true if key was newly 
	inserted into the list, false if key already existed

  delete(l,key): deletes any binding of key from the l. Returns
	false if key was not defined.

  search(l,key,&value): Searches for key in l and returns true if found.
	If found, the value associated with key is stored in the
	location pointed to by &value

*/


#define false 0
#define true 1
typedef char boolean;
#define BitsInRandom 31

#define allowDuplicates

#define MaxNumberOfLevels 16
#define MaxLevel (MaxNumberOfLevels-1)
// newNodeOfLevel生成一个nodeStructure结构体，同时生成l个node *数组指针
#define newNodeOfLevel(l) (node)malloc(sizeof(struct nodeStructure)+(l)*sizeof(node *))

typedef int keyType;
typedef int valueType;

#ifdef allowDuplicates
boolean delete(), search();
void insert();
#else
boolean insert(), delete(), search();
#endif

// 这里仅仅是一个指针
typedef struct nodeStructure *node;

typedef struct nodeStructure
{
    keyType key;	// key值
    valueType value;	// value值
    // 向前指针数组，根据该节点层数的
    // 不同指向不同大小的数组
    node forward[1];	
};

// 定义跳表数据类型
typedef struct listStructure{
   int level; 	  /* Maximum level of the list 
			(1 more than the number of levels in the list) */
   struct nodeStructure * header; /* pointer to header */
   } * list;

node NIL;

int randomsLeft;
int randomBits;

init() { 
	// 生成一个节点
  NIL = newNodeOfLevel(0);
  NIL->key = 0x7fffffff;
  randomBits = random();
  randomsLeft = BitsInRandom/2;
};

/*
 生成一个空的跳表数据结构
 */
list newList()
{
  list l;
  int i;
	// 申请list类型大小的内存
  l = (list)malloc(sizeof(struct listStructure));
  // 设置跳表的层level，初始的层为0层（数组从0开始）
  l->level = 0;
  
  // 生成header信息部分
  l->header = newNodeOfLevel(MaxNumberOfLevels);
  // 将header的forward数组清空
  for(i=0;i<MaxNumberOfLevels;i++) l->header->forward[i] = NIL;
  return(l);
}; 

freeList(l) 
  list l; 
  {
  register node p,q;
  p = l->header;
  do {
    q = p->forward[0];
    free(p);
    p = q; }
    while (p!=NIL);
  free(l);
  };

int randomLevel()
  {register int level = 0;
   register int b;
   do {
    b = randomBits&3;
    if (!b) level++;
    randomBits>>=2;
    if (--randomsLeft == 0) {
        randomBits = random();
        randomsLeft = BitsInRandom/2;
        };
    } while (!b);
    return(level>MaxLevel ? MaxLevel : level);
    };

////////////////////////////////////////////////////
// 插入一个节点
boolean insert(l,key,value) 
	register list l;
	register keyType key;
	register valueType value;
{
  register int k;
  // 使用了update数组
  node update[MaxNumberOfLevels];
  register node p,q;

  p = l->header;
  k = l->level;
  /*******************1*********************/
  do {
		// 查找插入位置
		while (q = p->forward[k], q->key < key)
			p = q;
		
		// 设置update数组
		update[k] = p;
	} while(--k>=0);	// 对于每一层进行遍历
	
	// 这里已经查找到了合适的位置，并且update数组已经
	// 填充好了元素
  if (q->key == key)
  {
    q->value = value;
		return(false);
	};
	
	// 随机生成一个层数
  k = randomLevel();  
 	if (k>l->level) 
  {
  	// 如果新生成的层数比跳表的层数大的话
    // 增加整个跳表的层数
		k = ++l->level;
		// 在update数组中将新添加的层指向l->header
		update[k] = l->header;
	};
		
	/*******************2*********************/
	// 生成层数个节点数目
  q = newNodeOfLevel(k);
  q->key = key;
  q->value = value;
      
	// 更新两个指针域
  do 
  {
		p = update[k];
		q->forward[k] = p->forward[k];
		p->forward[k] = q;
	} while(--k>=0);
	
	// 如果程序运行到这里，程序已经插入了该节点

  return(true);
}
////////////////////////////////////////////////
// 删除函数
boolean delete(l,key) 
register list l;
register keyType key;
{
  register int k,m;
  // 生成一个辅助数组update
  node update[MaxNumberOfLevels];
  register node p,q;

  p = l->header;
  k = m = l->level;
  // 这里和查找部分类似，最终update中包含的是：
  // 指向该节点对应层的前驱节点
  do 
  {
		while (q = p->forward[k], q->key < key) 
			p = q;
			update[k] = p;
	} while(--k>=0);

	// 如果找到了该节点，才进行删除的动作
  if (q->key == key) 
  {
  	// 指针运算
		for(k=0; k<=m && (p=update[k])->forward[k] == q; k++) 
			// 这里可能修改l->header->forward数组的值的 
		  p->forward[k] = q->forward[k];
		// 释放实际内存
		free(q);
		
		// 如果删除的是最大层的节点，那么需要重新维护跳表的
		// 层数level
   	while( l->header->forward[m] == NIL && m > 0 )
	     m--;
		l->level = m;
		return(true);
	}
  else
  	// 没有找到该节点，不进行删除动作 
  	return(false);
}

//////////////////////////////////////////////////
// 查找
boolean search(l,key,valuePointer)
register list l;
register keyType key;
valueType * valuePointer;
  {
  register int k;
  register node p,q;
  p = l->header;
  k = l->level;
  
  
  do 
  {
  	while (q = p->forward[k], q->key < key) 
  		p = q;
  }
  while (--k>=0);
  // 这里查找到的值是大于或者是等于需要查找的key值的
  if (q->key != key) return(false);
  *valuePointer = q->value;
  return(true);
  };

#define sampleSize 65536
main() {
  list l;
  register int i,k;
  keyType keys[sampleSize];
  valueType v;

  init();

  l= newList();

  for(k=0;k<sampleSize;k++) {
        keys[k]=random();
        insert(l,keys[k],keys[k]);
        };


  for(i=0;i<4;i++) {
        for(k=0;k<sampleSize;k++) {
	    if (!search(l,keys[k],&v)) printf("error in search #%d,#%d\n",i,k);
	    if (v != keys[k]) printf("search returned wrong value\n");
            };
        for(k=0;k<sampleSize;k++) {
	    if (! delete(l,keys[k])) printf("error in delete\n");
            keys[k] = random();
	    insert(l,keys[k],keys[k]);
            };
        };

  freeList(l);

  };