回归分析（regression analysis)

名词解释：

它基于观测数据建立变量间适当的依赖关系，以分析数据内在规律，并可用于预报、控制等问题。

回归分析是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法。运用十分广泛，回归分析按照涉及的自变量的多少，可分为一元回归分析和多元回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

应用理解：

已知多个观测数据（x，y），想找到x和y之间的一种函数的对应关系，y=f（x）；一般先通过画（x，y）的散点图，先进行直观（就是看）的分析，若x和y之间大题呈现一条直线，则可以认为x和y之间是一种线性的函数关系，则用一次函数（简单的线性函数）f（x）=ax+b，来具体化x和y的函数关系，称为线性回归分析；若散点图的直观（就是看）的分析，x和y大体上不是直线关系，而是一种曲线走向，则此时用非线性函数，例如二次函数，指数函数，对数函数具体化x和y的关系能够更好“估计”x和y的真实关系。

实例讲解分析：

http://wenku.baidu.com/view/bc43d7d7f8c75fbfc77db29c.html

课程案例讲解：

本题给出的是50个数据样本点，其中x为这50个小朋友到的年龄，年龄为2岁到8岁，年龄可有小数形式呈现。Y为这50个小朋友对应的身高，当然也是小数形式表示的。现在的问题是要根据这50个训练样本，估计出3.5岁和7岁时小孩子的身高。

通过画出训练样本点的分布凭直觉可以发现这是一个典型的线性回归问题。

已知50个样本点（Xi，Yi），求直线函数Y=aX+b的最佳参数a，b；使其为x和y线性关系的最佳估计参数。

求解方法：

1，理论分析法，通过样本矩阵的运算，直接求解参数a，b。具体参见最小二乘回归分析。

此法具有速度快，结果优的优点。

2，优化法（梯度下降法）

随机初始a和b的值，然后计算所有样本的误差值的平方和error，作为损失函数J（a，b），通过优化算法——梯度下降法，修改参数a，b；然后再次计算error，然后再次调节a，b值，如此循环迭代调节，最后算法会收敛到一个最小值（有时局部最小值），即为一个使error项最小的参数a，b组合。

 

具体过程及代码参见：

Andrew ng的课程

http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex2/ex2.html

参考tornadomeet原文，

http://www.cnblogs.com/tornadomeet/archive/2013/03/15/2961660.html

 

梯度下降算法分析：

经过理论分析的算法一和梯度算法二，所得的最终a，b参数值不同，但是预测时两个的预测值是相同的；也就是说，存在a，b的不同组合使Y=aX+b的估计结果“满意“；

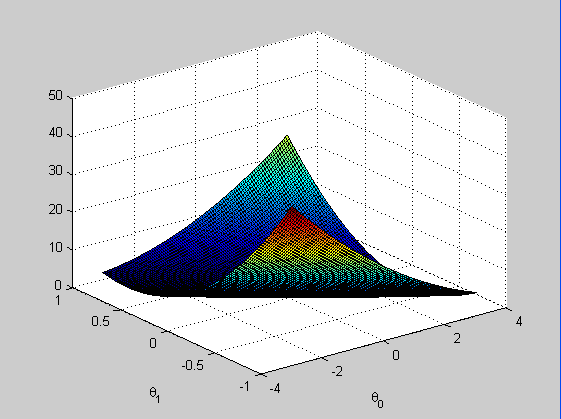
例如上图为误差平方和函数，即损失函数J（a，b）的三维图像，损失值随着a，b变化的走向图；

从中可以看出函数J为一个凸函数（大多数为让人头痛的非凸函数），所以通过梯度下降算法可以得到一个全局的最优解。

这里估计有人会提问了，既然理论分析算法一，可以快速高效的得到最好的a，b组合，为什么还要用复杂的梯度下降算法来计算呢。其实这里就是我想要重点介绍的了，因为美丽的理论分析算法，虽然严谨但是普适性很差，智能应用在线性拟合，对于一些非线性拟合，或者更复杂的问题，则只能干瞪眼了，如果拿手机来做个类比的化，那就是手机中的魅族了，小而美；而梯度下降算法，具有很强的普遍性，由于其把一个类似估计拟合的问题，转化成为一个优化误差平方和，求误差平方和极小值问题，而优化求极小值问题中梯度下降算法是一个经典实用的算法（也存在问题，以后在详述），故可以很容易的求解问题。