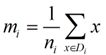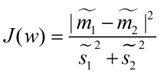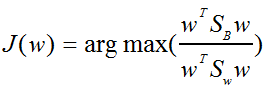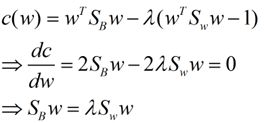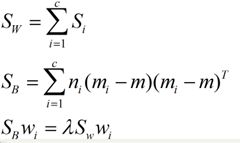线性判别分析（LDA）

      上一节介绍了PCA算法，PCA的目标是希望降维后的数据能够保持最多的信息，而Discriminant Analysis所追求的目标与PCA不同，它希望数据在降维后能够很容易地被区分开来。     

一． LDA算法概述：

     线性判别式分析(Linear Discriminant Analysis, LDA)，也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD)，是模式识别的经典算法，它是在1996年由Belhumeur引入模式识别和人工智能领域的。性鉴别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。因此，它是一种有效的特征抽取方法。使用这种方法能够使投影后模式样本的类间散布矩阵最大，并且同时类内散布矩阵最小。就是说，它能够保证投影后模式样本在新的空间中有最小的类内距离和最大的类间距离，即模式在该空间中有最佳的可分离性。

二. 原理简述：

     LDA的原理是，将带上标签的数据（点），通过投影的方法投影到维度更低的空间中，使得投影后的点形成按类别区分的情形，即相同类别的点，在投影后的空间中距离较近，不同类别的点，在投影后的空间中距离较远。

      要说明LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：

     当满足条件：对于所有的j，都有Yk > Yj,的时候，我们就说x属于类别k。对于每一个分类，都会用一个公式去计算一个得分值，所有公式的结果中得分最高的那个类别，就是所属的分类了。

    上式实际上就是一种投影，是将一个高维的点投影到一条高维的直线上，LDA最求的目标是，给出一个标注了类别的数据集，投影到了一条直线之后，能够使得点尽量的按类别区分开，当k=2即二分类问题的时候，如下图所示：

     红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点，经过原点的那条线就是投影的直线，从图上可以清楚的看到，红色的点和蓝色的点被原点明显的分开了，这个数据只是随便画的，如果在高维的情况下，看起来会更好一点。下面我来推导一下二分类LDA问题的公式：

     假设用来区分二分类的直线（投影函数)为：

    LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好，所以我们需要定义几个关键的值。

    类别i的原始中心点为：（Di表示属于类别i的点)

    类别i投影后的中心点为：

    衡量类别i投影后，类别点之间的分散程度（方差）为：

    最终我们可以得到一个下面的公式，表示LDA投影到w后的损失函数：

   我们分类的目标是，使得类别内的点距离越近越好（集中），类别间的点越远越好。分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散，分子为两个类别各自的中心点的距离的平方，我们最大化J(w)就可以求出最优的w了。想要求出最优的w，可以使用拉格朗日乘子法，但是现在我们得到的J(w)里面，w是不能被单独提出来的，我们就得想办法将w单独提出来。

   我们定义一个投影前的各类别分散程度的矩阵，这个矩阵的意思是，如果某一个输入点集Di里面的点距离这个分类的中心点mi越近，则Si里面元素的值就越小，如果分类的点都紧紧地围绕着mi，则Si里面的元素值越更接近0.

   带入Si，将J(w)分母化为：

   同样的将J(w)分子化为：

   这样损失函数可以化成下面的形式，我们的目标是求取它的最大值：

   这样就可以用拉格朗日乘子法了，但是还有一个问题，如果分子、分母是都可以取任意值的，那就会使得有无穷解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧），并作为拉格朗日乘子法的限制条件，带入得到：

求导公式如下：

   这样的式子就是一个求特征值的问题了。

   对于N(N>2)分类的问题，我就直接写出下面的结论了：

 又因为w=[w1,w2...wd]，所以得到：

把损失函数分解可知，我们要求的是:

       最佳投影矩阵的列向量即为的d个最大的特征值所对应的特征向量(矩阵的特征向量)，且最优投影轴的个数d<=c-1(c表示类的个数).

   这里想多谈谈特征值，特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用，特征值表示的是矩阵的性质，当我们取到矩阵的前N个最大的特征值的时候，我们可以说提取到的矩阵主要的成分（这个和之后的PCA相关，但是不是完全一样的概念）。在机器学习领域，不少的地方都要用到特征值的计算，比如说图像识别、pagerank、LDA、还有之后将会提到的PCA等等。

 

 

三. 使用LDA的一些限制

 1、 LDA至多可生成C-1维子空间

      

     由于中的 秩为1，因此的秩至多为C（矩阵的秩小于等于各个相加矩阵的秩的和）。由于知道了前C-1个后，最后一个可以有前面的来线性表示，因此的秩至多为C-1。那么K最大为C-1，即特征向量最多有C-1个。特征值大的对应的特征向量分割性能最好。

 2、 LDA不适合对非高斯分布样本进行降维。

      

   上图中红色区域表示一类样本，蓝色区域表示另一类，由于是2类，所以最多投影到1维上。不管在直线上怎么投影，都难使红色点和蓝色点内部凝聚，类间分离。

 3、 LDA在样本分类信息依赖方差而不是均值时，效果不好。

      

  上图中，样本点依靠方差信息进行分类，而不是均值信息。LDA不能够进行有效分类，因为LDA过度依靠均值信息。

 4、 LDA可能过度拟合数据。

四. LDA与PCA对比

   将3维空间上的球体样本点投影到二维上，W1相比W2能够获得更好的分离效果。

      

      PCA与LDA的降维对比：

      

      PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的方向。

参考：

1）http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html

2）http://blog.csdn.net/warmyellow/article/details/5454943